Угол между двумя прямыми (формула)

На этой странице вы найдете объяснение того, как рассчитать угол между двумя линиями (формула). Вы также сможете увидеть несколько примеров и, кроме того, сможете попрактиковаться, выполняя упражнения, решаемые шаг за шагом.

Каков угол между двумя прямыми?

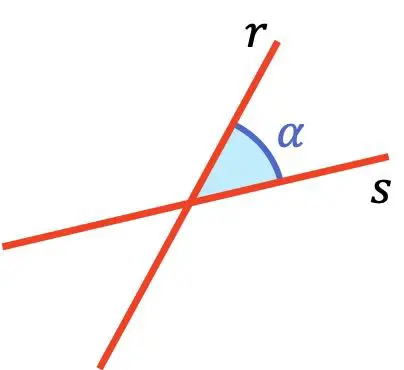
Угол между двумя линиями — это наименьший угол между этими двумя линиями.

В плане различают четыре типа линий в зависимости от угла, который они образуют между собой: пересекающиеся линии (между 0° и 90°), перпендикулярные линии (90°), параллельные линии (0°) и совпадающие линии (0°).

пересекающиеся линии

угол между двумя пересекающимися прямыми

Пересекающиеся линии пересекаются под острым углом от 0° до 90°.

Перпендикулярные прямые

угол между двумя перпендикулярными прямыми

Перпендикулярные линии пересекаются под прямым углом 90°.

Параллельные линии

Параллельные линии никогда не соприкасаются и образуют между собой угол 0°.

совпадающие линии

Две совпадающие прямые имеют все точки общие и, следовательно, между ними всегда существует угол 0°.

В заключение, расчет угла между двумя параллельными, совпадающими или перпендикулярными линиями выполняется немедленно: параллельные линии и совпадающие линии образуют угол 0 градусов, поскольку они имеют одинаковое направление, а перпендикулярные линии пересекаются под углом 90 градусов. . С другой стороны, чтобы найти угол между двумя пересекающимися прямыми, необходимо применить формулу (ее мы увидим ниже).

Как рассчитывается угол между двумя прямыми?

Есть два способа вычислить угол между двумя линиями. Первый метод использует вектор направления каждой линии, а второй метод основан на наклоне каждой линии.

Ни одна из процедур не лучше другой, на самом деле обе они довольно просты, но в зависимости от того, как выражены линии, практичным является тот или иной метод. Поэтому мы рекомендуем вам знать, как использовать оба математических метода.

Метод ориентации линейного вектора

Формула для расчета угла между двумя линиями с использованием их векторов направления:

Учитывая векторы направления двух разных линий:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

Угол между этими двумя линиями можно рассчитать по следующей формуле:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Золото

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

являются модулями векторов

$\vv{\text{u}}$

$\vv{\text{v}}$

соответственно.

Помните, что формула величины вектора:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Давайте посмотрим, как найти угол между двумя прямыми на примере:

Вычислите угол между следующими двумя линиями:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

Чтобы вычислить угол между двумя линиями, сначала необходимо найти вектор направления каждой линии.

право

$r$

выражается в виде параметрического уравнения , поэтому компонентами вектора, отмечающего его направление, являются:

$\vv{r} = (-3,4)$

и закон

$\displaystyle s$

определяется в виде неявного (или общего) уравнения, поэтому координаты его вектора направления равны:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Теперь, когда мы знаем вектор направления каждой линии, мы можем использовать формулу угла между двумя линиями:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Поэтому мы определяем величину двух векторов:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

Выполним векторные операции формулы угла:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

И, наконец, вычисляем угол, образованный двумя прямыми с обратным косинусом:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

Помните, что вычислить обратную величину косинуса можно с помощью калькулятора с ключом

$\boxed{\cos ^{-1}}.$

метод наклона

Очевидно, чтобы понять этот метод, нужно знать наклон линии . Ознакомиться с этим понятием можно по ссылке, где вы найдете подробное объяснение, что оно означает, как рассчитывается, примеры и решения упражнений наклона линии.

Формула расчета угла между двумя линиями по их наклонам:

Или две отдельные строки:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

Угол между этими двумя линиями можно определить по следующей формуле:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Золото

$m_1$

$m_2$

наклоны линий

$r_1$

$r_2$

соответственно.

Давайте посмотрим, как вычислить угол между двумя линиями, используя их наклоны, на примере:

Найдите угол между следующими двумя прямыми:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

Наклон каждой строки — это число перед переменной.

$x:$

$m_r = 4$

$m_s = -3$

Следовательно, угол между двумя линиями можно найти, применив формулу наклона:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

И, наконец, находим угол, обратный тангенсу:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

Помните, что вычислить обратную величину тангенса можно с помощью калькулятора с ключом

$\boxed{\tan ^{-1}}.$

Мы только что видели пример с наклонами двух линий, выраженными в виде явного уравнения, но если бы они были в форме уравнения наклона точки, пришлось бы использовать ту же самую процедуру.

Решение проблем с углом между двумя линиями

Упражнение 1

Определите угол, образованный следующими двумя прямыми:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

посмотреть решение

В этом случае мы будем использовать метод вектора направления. Следовательно, мы должны сначала найти вектор направления каждой линии. Обе линии выражаются в виде параметрических уравнений, поэтому компонентами их векторов направления являются члены перед параметром

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Поэтому мы определяем величину двух векторов:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

Решаем скалярное произведение двух векторов числителя и умножение модулей знаменателя:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

И, наконец, мы находим угол, образованный двумя прямыми, производя обратный косинус:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Упражнение 2

Найдите угол между следующими двумя прямыми:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

посмотреть решение

Эту задачу мы будем решать методом вектора направления, поэтому сначала нам нужно найти вектор направления каждой линии. право

$r$

выражается в форме общего (или неявного) уравнения, такого, что компоненты вектора, указывающие его направление:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

и закон

$\displaystyle s$

определяется в виде непрерывного уравнения, поэтому декартовыми координатами его вектора направления являются числа знаменателей:

$\vv{s} = (6,3)$

Зная вектор направления каждой линии, мы можем использовать формулу угла между двумя линиями:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Поэтому мы определяем модули двух векторов:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

Проведем операции между векторами формулы угла:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

И, наконец, вычисляем угол, образованный двумя прямыми с обратным косинусом:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Упражнение 3

Каков угол между следующими двумя линиями?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

посмотреть решение

В этом случае воспользуемся методом наклонов линий, чтобы узнать угол, который они составляют, так как линии имеют вид явного уравнения.

Наклон каждой линии — это число, которое сопровождает независимую переменную.

$x:$

$m_r = -2$

$m_s = 5$

Следовательно, угол между двумя линиями можно определить, применив формулу наклона:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

И, наконец, мы находим угол между двумя линиями, меняя касательную:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Упражнение 4

Найдите уравнение прямой, проходящей через точку

$P(5,-1)$

и составляет угол 45° с линией

$r.$

Скажем, строка:

$\displaystyle r: \ y=2x+4$

посмотреть решение

Для решения проблемы мы позвоним

$s$

вправо, которую мы собираемся вычислить. Кроме того, мы будем использовать метод наклона, поскольку мы знаем наклон линии.

$r:$

$m_r=2$

Из формулы угла между двумя линиями (метод наклона) можно получить значение наклона линии

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

Подставляем известные значения в формулу:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

И попробуем решить полученное уравнение:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

Абсолютное значение уравнения несколько затрудняет его решение, поскольку приходится анализировать как положительные, так и отрицательные варианты:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

Таким образом, у нас есть два возможных решения: линия с наклоном -3 и другая линия с наклоном в одну треть.

Формула уравнения точки-наклона линии:

$y-y_0=m(x-x_0)$

Следовательно, как только мы знаем наклон двух возможных линий, мы можем написать уравнение наклона точки каждой линии с точкой, через которую они должны пройти в соответствии с утверждением:

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

Угол между двумя линиями (формула)

Каков угол между двумя прямыми?

Как рассчитывается угол между двумя прямыми?

Метод ориентации линейного вектора

метод наклона

Решение проблем с углом между двумя линиями

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Оставьте комментарий Отменить ответ