На этой странице объясняется, каковы точки пересечения (или пересечения) функции с декартовыми осями и как их вычислять. Кроме того, вы найдете несколько примеров, чтобы полностью понять, как они находятся, и даже сможете попрактиковаться, выполняя упражнения, решаемые шаг за шагом.
Каковы точки пересечения (или пересечения) функции с осями?
Прежде чем посмотреть, как они рассчитываются, давайте вспомним, что такое точки пересечения функции с осями.
Точки пересечения или пересечения осей — это точки, в которых представление функции пересекает оси координат, то есть точки на графике, связывающие ось X и ось l. Ось Y.
Например, парабола на следующем графике пересекает ось Y в точке (0,3) и ось X в точках (-1,0) и (3,0).
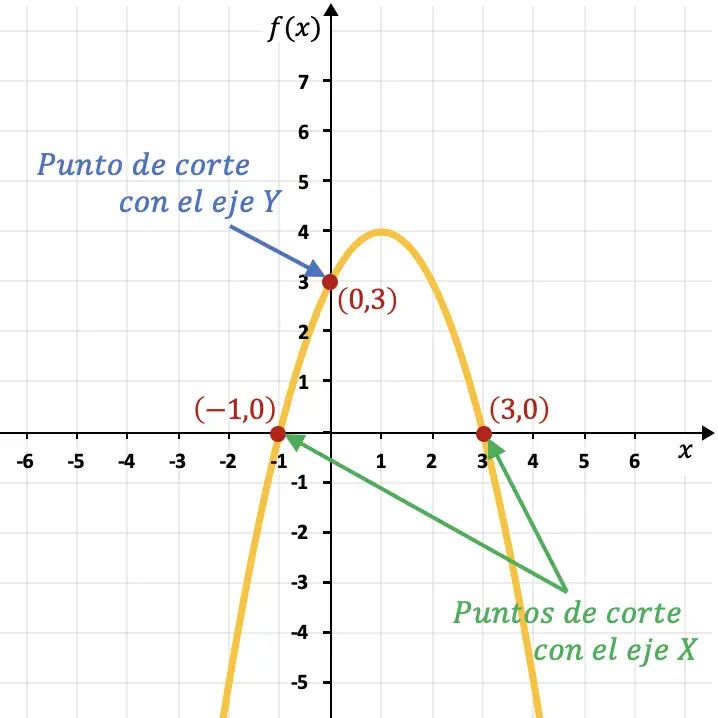
Точка разреза функции по оси X
Вторая координата точек пересечения функции с осью X всегда будет равна 0, следовательно:
Точки отсечения любой функции OX оси X имеют вид
![]()
, и его можно рассчитать, решив следующее уравнение:
![]()
Иногда при решении этого уравнения мы можем получить два (или более) решения, это означает, что функция пересекает ось X два (или более) раза. С другой стороны, если уравнение не имеет решения, это означает, что функция не пересекает ось X.
Точка разреза функции по оси Y
Первая координата точек пересечения функции с осью Y всегда будет равна 0, следовательно:
Точка отсечки любой функции с осью Y OY имеет вид
![]()
, и его можно найти, вычислив образ функции в точке x=0:
![]()
В отличие от точек останова по оси X, по оси Y может быть только одна точка останова.
Пример расчета точек среза функции с осями
Чтобы у вас не осталось сомнений, ниже мы увидим пример того, как найти точки разреза функции с декартовыми осями:
- Найдите численно точки среза следующей функции:
![]()
Сначала мы рассчитаем точку отсечки функции по оси X. Точка пересечения с осью X всегда будет иметь вторую компоненту, равную 0, то есть она будет типа
![]()
. Потому что f(x) всегда равна 0 по оси OX. Итак, чтобы найти другую составляющую точки, нам нужно решить уравнение
![]()
![]()
![]()
![]()
![]()
Таким образом, точка пересечения с осью X равна:
![]()
Теперь найдем точку пересечения с осью Y. Точка пересечения с осью Y всегда будет иметь первую компоненту, равную 0, то есть точка будет типа
![]()
. Поскольку независимая переменная x всегда сокращается по оси Y. Итак, чтобы найти другую координату точки, нам нужно вычислить
![]()
![]()
Таким образом, точка пересечения с осью Y равна:
![]()
Ниже приведен графический пример функции, вы можете видеть, что найденные пороговые значения совпадают с указанными на графике:
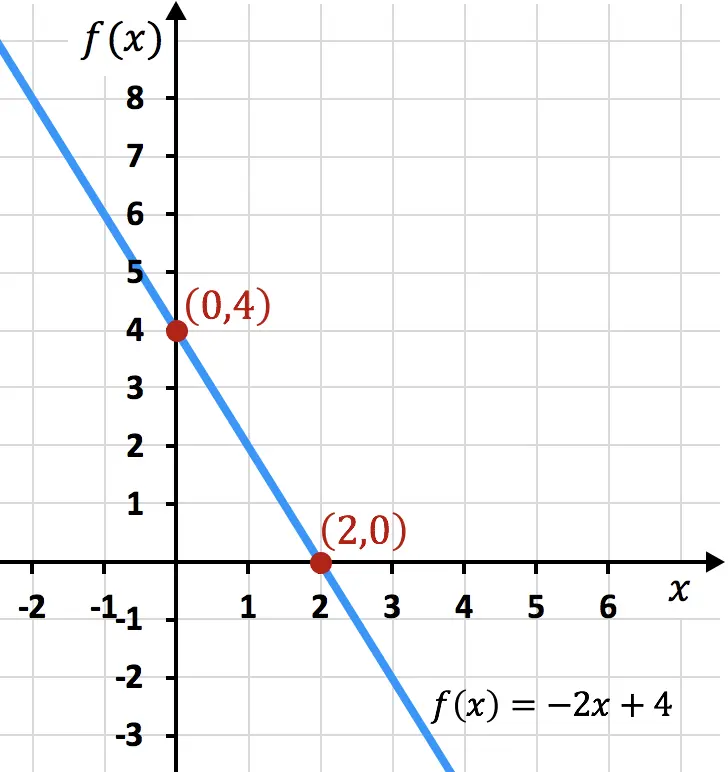
Решенные упражнения для точек разреза функции с осями
Упражнение 1
Определите точки резания с осями координат следующей функции:
![]()
Точка резки по оси X
Чтобы найти точку пересечения функции с осью X необходимо решить
![]()
![]()
![]()
![]()
![]()
Таким образом, точка пересечения функции с осью X равна:
![]()
Точка резки по оси Y
Чтобы найти точку пересечения с осью Y, необходимо вычислить
![]()
![]()
Таким образом, точка пересечения функции с осью Y равна:
![]()
Упражнение 2
Найдите точки пересечения с декартовыми осями следующей аффинной функции:
![]()
Точка резки по оси X
Чтобы найти предельную точку функции с осью OX, нам нужно положить функцию равной нулю и решить полученное уравнение:
![]()
![]()
![]()
![]()
Итак, точка пересечения функции с осью абсцисс равна:
![]()
Точка резки по оси Y
Чтобы найти точку отсечки с осью OY, нам нужно вычислить
![]()
![]()
Таким образом, точка пересечения функции с осью компьютера равна:
![]()
Упражнение 3
Рассчитайте точки отсечки с помощью осей следующей квадратичной функции:
![]()
Точка резки по оси X
Чтобы найти точку пересечения функции с осью X необходимо решить
![]()
![]()
![]()
В данном случае нам необходимо решить квадратное уравнение, поэтому применим формулу:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47048fdd48ce98ba99629edf5a379f76_l3.png)
Мы получили два решения квадратного уравнения, поэтому функция пересекает ось X в двух точках:
![]()
Точка резки по оси Y
С другой стороны, чтобы определить точку пересечения с осью Y, необходимо вычислить
![]()
![]()
Следовательно, единственной точкой пересечения функции с осью Y является:
![]()
Упражнение 4
Найдите точки пересечения с осями декартовой плоскости следующей рациональной функции:
![]()
Точка резки по оси X
Чтобы найти точку пересечения функции с осью X необходимо решить
![]()
![]()
![]()
![]()
![]()
![]()
5 не эквивалентно 0, поэтому уравнение не имеет решения и, следовательно, нет точки пересечения функции и оси X.
Точка резки по оси Y
Чтобы найти точку пересечения с осью Y, необходимо вычислить
![]()
![]()
Любое число, разделенное на ноль, представляет собой неопределенность, дающую бесконечность. Следовательно, функция ни в какой точке не выходит за пределы оси Y.
Короче говоря, функция упражнения не имеет точек пересечения с осями , то есть ее график не проходит ни через ось X, ни через ось Y ни в одной точке.
Упражнение 5
Рассчитайте точки отсечки с помощью осей следующей функции третьей степени:
![]()
Точка резки по оси X
Чтобы найти точку пересечения функции с осью X необходимо решить
![]()
![]()
![]()
Оба члена уравнения имеют x , с помощью которого мы можем извлечь общий множитель:
![]()
Чтобы предыдущее равенство выполнялось, один из факторов должен быть равен 0. Поэтому мы приравниваем каждый фактор к нулю, чтобы получить все возможные решения:
![Rendered by QuickLaTeX.com \displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-37febaed85a502533604305b9009611d_l3.png)
Таким образом, мы получили три решения уравнения третьей степени, поэтому функция разрезает ось X в 3 точках:
![]()
Точка резки по оси Y
Чтобы рассчитать точку разреза по оси Y, необходимо вычислить
![]()
![]()
Следовательно, единственной точкой пересечения функции с осью Y является начало координат (0,0):
![]()
Обратите внимание, что мы уже нашли эту точку при расчете точки разреза по оси X, потому что функция режет в этой точке обеими осями одновременно.