Теорема Руша – Фребениуса

На этой странице мы узнаем, что такое теорема Руше Фробениуса и как с ее помощью вычислить ранг матрицы. Вы также найдете примеры и упражнения, пошагово решаемые с помощью теоремы Руше-Фробениуса.

Что такое теорема Руше–Фробениуса?

Теорема Руше-Фробениуса — это метод классификации систем линейных уравнений. Другими словами, теорема Руше-Фробениуса используется для определения количества решений системы уравнений без необходимости ее решения.

Существует 3 типа систем уравнений:

Определяемая совместимость системы (SCD): система имеет уникальное решение.
Неопределенно-совместимая система (ICS): система имеет бесконечное количество решений.
Несовместимость системы (SI): система не имеет решения.

Кроме того, теорема Руше-Фробениуса позже позволит нам решать системы с помощью правила Крамера .

Формулировка теоремы Руше-Фробениуса

Теорема Руше-Фробениуса гласит, что

$\displaystyle \bm{A}$

– матрица, образованная коэффициентами при неизвестных системы уравнений. и живот

$\displaystyle \bm{A'}$

, или расширенная матрица , представляет собой матрицу, образованную коэффициентами неизвестных системы уравнений и независимыми членами:

Теорема Руше-Фробениуса позволяет нам узнать, с какой системой уравнений мы имеем дело, в зависимости от ранга матриц A и A’:

Если ранг(A) = ранг(A’) = количество неизвестных ⟶ Определенная совместимая система (SCD).
Если ранг(A) = ранг(A’) <количество неизвестных ⟶ Неопределенно-совместимая система (SCI).
если диапазон (А)
$\bm{\neq}$

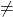
диапазон (A’) ⟶ Несовместимая система (SI)

Как только мы узнаем, что говорит теорема Руше-Фробениуса, мы увидим, как решать упражнения по теореме Руше-Фробениуса. Вот 3 примера: упражнение, решенное с использованием теоремы каждого типа системы уравнений.

Пример определенной совместимой системы (SCD)

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

Матрица A и расширенная матрица A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

Теперь вычислим ранг матрицы А. Для этого проверим, отличается ли определитель всей матрицы от 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

Поскольку определитель матрицы 3×3 отличается от 0, матрица A имеет ранг 3:

$\displaystyle rg(A)=3$

Как только мы узнаем ранг A, мы вычисляем ранг A’, который будет не ниже ранга 3, поскольку мы только что видели, что он имеет внутри определитель порядка 3, отличный от 0. Более того, он не может иметь ранг 4, так как мы не можем сделать ни одного определителя порядка 4. Следовательно, матрица А’ также имеет ранг 3:

$\displaystyle rg(A')=3$

Таким образом, поскольку ранг матрицы A равен рангу матрицы A’ и числу неизвестных системы (3), мы знаем по теореме Руше Фробениуса, что это совместимая детерминированная система (SCD). :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Пример неопределенно совместимой системы (ICS)

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

Матрица A и расширенная матрица A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

Теперь вычислим ранг матрицы А. Для этого проверим, отличается ли определитель всей матрицы от 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

Определитель всей матрицы A дает 0, поэтому она не имеет ранга 3. Чтобы проверить, имеет ли она ранг 2, мы должны найти в A подматрицу, определитель которой отличен от 0. Например, та, что находится в верхнем левом углу :

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Поскольку определитель матрицы 2×2 отличается от 0, матрица A имеет ранг 2:

$\displaystyle rg(A)=2$

Зная ранг A, мы вычисляем ранг A’. Мы уже знаем, что определитель первых трех столбцов дает 0, поэтому пробуем другие возможные определители 3×3:

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

Все определители 3×3 матрицы A’ равны 0, поэтому матрица A’ также не будет иметь ранг 3. Однако внутри него есть определители порядка 2, отличного от 0. Например:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Таким образом , матрица A’ будет иметь ранг 2 :

$\displaystyle rg(A')=2$

Размер матрицы A равен размеру матрицы A’, но он меньше числа неизвестных системы (3). Следовательно, согласно теореме Руше-Фробениуса, это неопределенно-совместная система (ИНС):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Пример несовместимой системы (IS)

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

Матрица A и расширенная матрица A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

Теперь вычислим ранг матрицы А. Для этого проверим, отличается ли определитель всей матрицы от 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

Поскольку матрица имеет определитель порядка 2, отличный от 0, матрица A имеет ранг 2:

$\displaystyle rg(A)=2$

Зная ранг A, мы вычисляем ранг A’. Мы уже знаем, что определитель первых 3-х столбцов дает 0, поэтому теперь попробуем, например, с определителем последних 3-х столбцов:

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

С другой стороны, матрица A’ содержит определитель, результат которого отличен от 0, поэтому матрица A’ будет иметь ранг 3 :

$\displaystyle rg(A')=3$

Следовательно, поскольку ранг матрицы A меньше ранга матрицы A’, мы выводим из теоремы Руше-Фробениуса, что это несовместимая система (SI) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Решенные задачи теоремы Руше–Фробениуса

Упражнение 1

Определите тип следующей системы уравнений с тремя неизвестными, используя теорему Руше-Фробениуса:

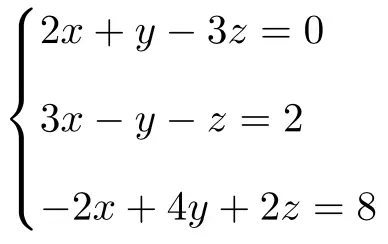
Решение упражнения теоремы Руша - Фробениуса

посмотреть решение

Сначала мы создаем матрицу A и расширенную матрицу A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

Теперь мы должны найти ранг матрицы А. Для этого проверяем, отличается ли определитель матрицы от 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

Матрица, имеющая определитель третьего порядка, отличный от 0, матрица А имеет ранг 3:

$\displaystyle rg(A)=3$

Зная ранг A, мы вычисляем ранг A’. Это будет как минимум ранг 3, потому что мы только что видели, что внутри него есть определитель порядка 3, отличного от 0. Более того, он не может иметь ранга 4, поскольку мы не можем не создать определитель 4×4. Следовательно, матрица A’ также имеет ранг 3:

$\displaystyle rg(A')=3$

Таким образом, благодаря теореме Руше-Фробениуса мы знаем, что это детерминированная совместимая система (ДСК), поскольку диапазон А равен диапазону А’ и числу неизвестных.

Упражнение 2

Классифицируйте следующую систему уравнений с тремя неизвестными, используя теорему Руше-Фробениуса:

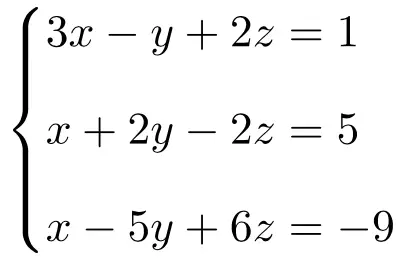
Решенное упражнение теоремы Руша-Фробениуса

посмотреть решение

Сначала построим матрицу A и расширенную матрицу A’ системы:

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

Теперь вычислим диапазон матрицы A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

Итак, матрица A имеет ранг 2:

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

Все определители 3×3 матрицы A’ равны 0, поэтому матрица A’ также не будет иметь ранг 3. Однако внутри него имеется множество определителей порядка 2, отличного от 0. Например:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

Таким образом , матрица A’ будет иметь ранг 2 :

$\displaystyle rg(A')=2$

Ранг матрицы A равен рангу матрицы A’, но эти два меньше числа неизвестных системы (3). Следовательно, по теореме Руше-Фробениуса мы знаем, что это неопределенно-совместная система (ИНС):

Упражнение 3

Определите, к какому типу системы относится следующая система уравнений, используя теорему Руше-Фробениуса:

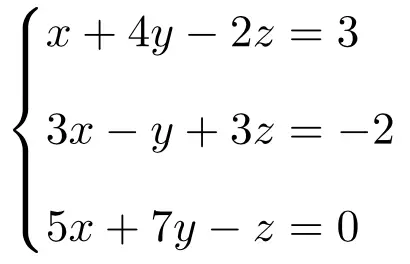
упражнение решается пошагово по теореме Руша - Фробениуса

посмотреть решение

Сначала мы создаем матрицу A и расширенную матрицу A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

Теперь вычислим диапазон матрицы A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

Итак, матрица A имеет ранг 2:

$\displaystyle rg(A)=2$

Зная ранг A, мы вычисляем ранг A’. Мы уже знаем, что определитель первых трех столбцов дает 0, но не определитель последних трех столбцов:

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

Следовательно, матрица A’ имеет ранг 3 :

$\displaystyle rg(A')=3$

Ранг матрицы A меньше ранга матрицы A’, поэтому из теоремы Руше-Фробениуса мы можем сделать вывод, что это несовместимая система (SI) :

Упражнение 4

Определите тип следующей системы уравнений с тремя неизвестными, используя теорему Руше-Фробениуса:

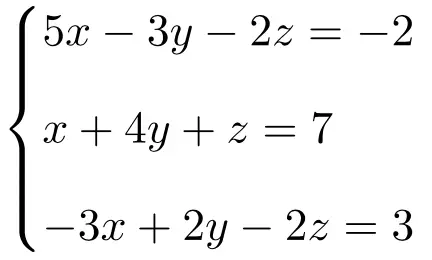
Решение теоремы Руша - Фробениуса с 3 неизвестными и 3 уравнениями

посмотреть решение

Сначала мы создаем матрицу A и расширенную матрицу A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

Теперь нам необходимо вычислить ранг матрицы A. Для этого решим определитель матрицы по правилу Сарруса:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

Матрица, имеющая определитель третьего порядка, отличный от 0, матрица А имеет ранг 3:

$\displaystyle rg(A)=3$

Следовательно, матрица A’ также имеет ранг 3 , поскольку она всегда имеет ранг не ниже A и не может иметь ранг 4, поскольку мы не можем разрешить ни один определитель 4×4.

$\displaystyle rg(A')=3$

Таким образом, благодаря применению теоремы Руше-Фробениуса мы знаем, что система является совместимой детерминированной системой (SCD), поскольку диапазон A равен диапазону A’ и числу неизвестных.

Упражнение 5

Определите, к какому типу системы относится следующая система уравнений, используя теорему Руше-Фробениуса:

посмотреть решение

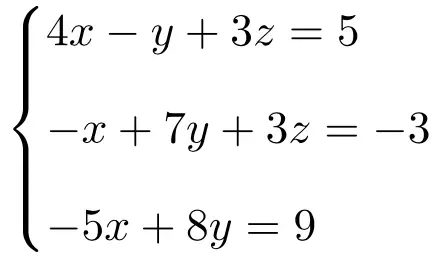
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

Теперь вычислим диапазон матрицы A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

Таким образом, матрица A имеет ранг 2:

$\displaystyle rg(A)=2$

Зная ранг A, мы вычисляем ранг A’. Определитель первых 3-х столбцов, который мы уже знаем, дает 0, а вот определитель последних 3-х столбцов не дает:

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

Следовательно, матрица A’ имеет ранг 3 :

$\displaystyle rg(A')=3$

И, наконец, мы применим область определения к теореме Руше-Фробениуса: область определения матрицы A меньше, чем область определения матрицы A’, поэтому это несовместимая система (SI) :

Упражнение 6

Классифицируйте следующую систему уравнений третьего порядка с учетом теоремы Руше-Фробениуса:

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

посмотреть решение

Сначала построим матрицу A и расширенную матрицу A’ системы:

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

Теперь вычислим диапазон матрицы A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Итак, матрица A имеет ранг 2:

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Таким образом , матрица A’ будет иметь ранг 2 :

$\displaystyle rg(A')=2$

Наконец, применяя теорему Руше-Фробениуса, мы знаем, что это неопределенная совместимая система (ICS), поскольку диапазон матрицы A равен диапазону матрицы A ‘, но эти два меньше, чем количество неизвестных в система(3):

Теорема руша – фребениуса

Что такое теорема Руше–Фробениуса?

Формулировка теоремы Руше-Фробениуса

Пример определенной совместимой системы (SCD)

Пример неопределенно совместимой системы (ICS)

Пример несовместимой системы (IS)

Решенные задачи теоремы Руше–Фробениуса

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Упражнение 6

Оставьте комментарий Отменить ответ