На этой странице вы найдете объяснение того, как происходит сложение полиномов. Кроме того, вы сможете увидеть примеры сумм полиномов и даже упражнения, решаемые шаг за шагом. Наконец, мы также объясним, каковы свойства этого типа операций с полиномами.
Как сложить многочлены?
В математике, чтобы сложить два или более многочленов, члены подобных многочленов должны быть сложены вместе. Другими словами, добавление полиномов состоит из добавления терминов, имеющих одинаковую буквальную часть (те же переменные и одинаковые показатели степени).
Таким образом, суммировать полиномы можно двумя разными способами: вертикальным методом или горизонтальным методом. Ниже приводится объяснение обеих процедур, но мы советуем вам сначала научиться складывать многочлены по вертикали, а затем переходить к горизонтальному методу. Очевидно, придерживайтесь того, который вы предпочитаете.
Добавление вертикальных полиномов
Далее мы увидим, как складываются два многочлена по вертикали на примере:
- Добавьте следующие два полинома:
![]()
![]()
Первое, что нам нужно сделать, это поместить один многочлен под другой так, чтобы одинаковые члены двух многочленов были выровнены по столбцам:
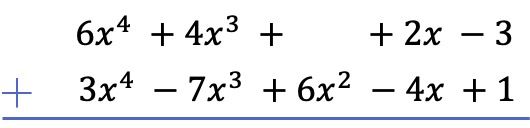
Внимание: если в полиноме нет члена определенной степени, место необходимо оставить пустым. Например
![]()
У вас нет одночлена 2 степени, поэтому на вашем сайте пустое место.
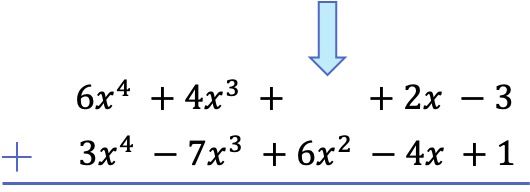
После того, как мы расположили все члены в порядке от высшей степени к низшей, мы добавляем коэффициенты в каждом столбце, сохраняя буквальные части равными:
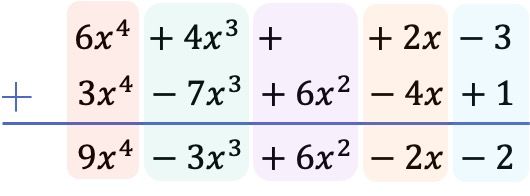
Следовательно, результат, полученный из суммы двух полиномов:
![]()
Теперь, когда вы понимаете, как складывать многочлены, знайте, что вы также можете складывать дроби, состоящие из многочленов. Этот тип операции называется сложением алгебраических дробей . Перейдите по этой ссылке и узнайте не только, как вычисляются суммы алгебраических дробей, но и как решаются все операции с алгебраическими дробями.
Горизонтальное сложение полиномов
Мы только что увидели, как складывать многочлены по вертикали, но теперь мы рассмотрим другой метод добавления многочленов: добавление многочленов по горизонтали. Конечно, эта процедура быстрее предыдущей, однако необходимо лучше владеть понятиями о полиномах.
Итак, давайте посмотрим, в чем состоит этот метод сложения полиномов на примере. И чтобы вы могли увидеть различия между двумя методами, мы добавим те же полиномы, что и в предыдущем примере:
- Вычислите сумму следующих двух полиномов:
![]()
![]()
Сначала вы должны разместить два полинома в одной операции, то есть один за другим:
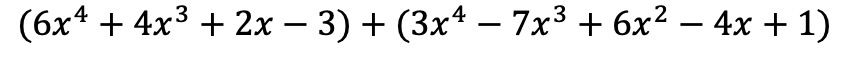
А теперь добавляем термины, имеющие одинаковые буквенные части, то есть термины с одинаковыми переменными (буквами) и одинаковыми показателями. Непохожие термины не могут быть добавлены.
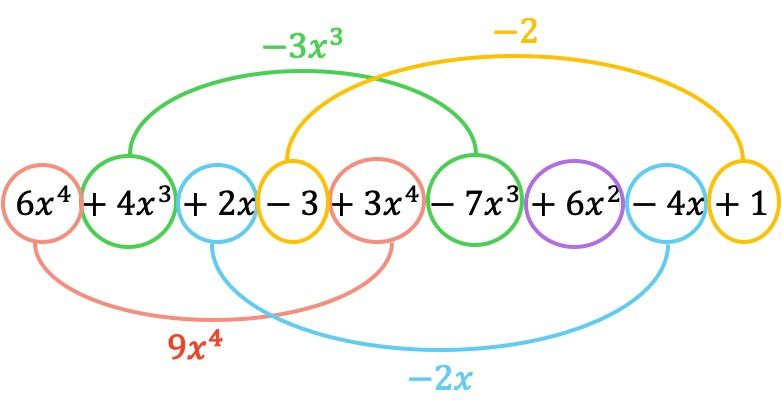
Таким образом, полином, полученный в результате сложения, равен:

Как видите, мы получили одинаковый результат обоими методами, поэтому при сложении полиномов вы можете использовать тот, который вам больше подходит.
Решенные задачи сложения полиномов
Чтобы вы могли попрактиковаться, мы оставляем вам несколько решенных упражнений на суммы полиномов. Если у вас есть вопросы, вы можете задать их в комментариях на странице и мы ответим на них в ближайшее время.
Упражнение 1
Добавьте следующие два полинома:
![]()
![]()
В этом случае мы добавим два полинома по вертикали. Для этого упорядочим многочлены по степени и сложим одночлены, расположенные в одном столбце:
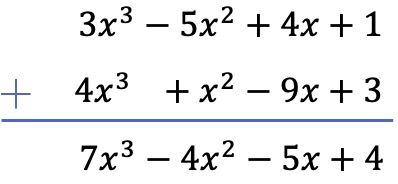
Упражнение 2
Решите сумму следующих двух многочленов:
![]()
![]()
Мы просуммируем два полинома, используя вертикальный метод. Поэтому мы упорядочиваем полиномы по степени и добавляем члены, расположенные в том же столбце:
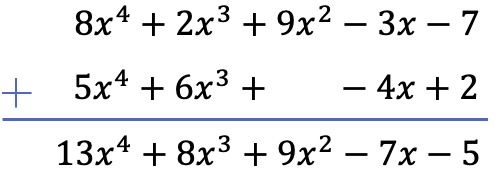
Обратите внимание, что в этом конкретном случае в столбце степени 2 второго многочлена необходимо оставить пустое место, поскольку он не имеет квадратичного члена.
Упражнение 3
Чему равна сумма следующих двух многочленов?
![]()
![]()
Мы выполним сложение двух полиномов вертикальным методом. ТАК:
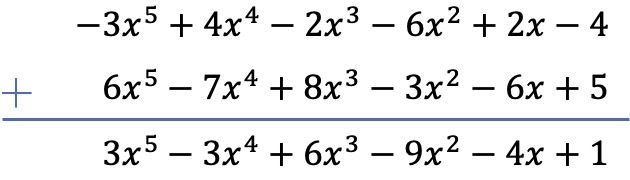
Упражнение 4
Вычислите сумму следующих трех многочленов:
![]()
![]()
![]()
Мы рассчитаем сумму трех полиномов, используя вертикальный метод. Поэтому мы упорядочиваем полиномы по степени и добавляем члены, расположенные в том же столбце:
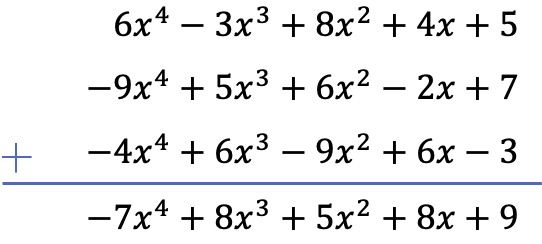
👉👉👉Теперь, когда вы увидели, как складываются два многочлена, вас может заинтересовать еще одна характерная операция многочленов: общий множитель. Извлечь из многочлена общий делитель довольно сложно (и трудно для понимания), ведь при этом допускаются многие ошибки. Именно поэтому мы подготовили руководство, в котором шаг за шагом объясняем, как извлечь общий делитель , чтобы вы прекрасно это поняли и не допустили ошибок при выполнении этой операции. Какие есть советы по извлечению общего делителя из многочлена, вы узнаете, перейдя по ссылке.
Свойства сложения полиномов
Сумма полиномов имеет следующие характеристики:
- Ассоциативное свойство : при добавлении 3 или более полиномов не имеет значения, как они сгруппированы, поскольку результат всегда один и тот же. То есть проверяется следующее равенство:
![]()
- Коммутативное свойство : при сложении многочленов порядок сложения не меняет результат сложения.
![]()
- Нейтральный элемент : очевидно, добавление полинома плюс любой другой полином с числовым значением, равным нулю, эквивалентно первому полиному.
![]()
- Противоположный элемент : результат сложения любого многочлена и противоположного ему многочлена всегда равен нулю.
![]()
Что вы думаете об объяснении? Вам это помогло? Какой метод сложения полиномов вы предпочитаете: вертикальный или горизонтальный? Читаем вас в комментариях! 👀