Здесь мы объясняем, что такое скорость изменения, средняя скорость изменения и мгновенная скорость изменения. Вы сможете увидеть несколько примеров того, как рассчитать скорость изменения, а также попрактиковаться с решенными пошаговыми упражнениями по скорости изменения.
Какова скорость изменения?
В математике скорость изменения (TV) функции — это разница значений функции в двух разных точках. Следовательно, чтобы вычислить скорость изменения между двумя точками, значения функции в этих двух точках необходимо вычесть.
![]()
Например, если два изображения функции имеют значения f(2)=1 и f(5)=7, скорость их изменения равна:
![]()
Мы только что увидели математический смысл скорости изменения, но в экономике понятие скорости изменения означает следующее:
В экономике скорость изменения двух величин — это разница между ними, выраженная в процентах, то есть скорость изменения переменной между разными периодами — это ее относительное изменение. Поэтому для расчета скорости изменения значения двух разных периодов вычитаются и полученный результат делится на значение начального периода.
![]()
Например, если стоимость определенных акций увеличится с 35 евро до 50 евро за один месяц, скорость ее изменения составит:
![]()
Учитывая два возможных значения скорости изменения, в этой статье мы сосредоточимся на понимании математического определения скорости изменения. Можно выделить два типа скорости изменения: среднюю скорость изменения и мгновенную скорость изменения. Ниже вы найдете объяснение каждого типа.
Средняя скорость изменения
Средняя скорость изменения (TVM) функции в интервале — это количество единиц, на которое функция увеличивается (или уменьшается) на каждую единицу, на которую увеличивается ее независимая переменная. Следовательно, средняя скорость изменения функции вычисляется путем деления роста функции на интервале на амплитуду этого же интервала.
![]()
Чтобы вы могли увидеть, как рассчитывается средняя скорость изменения, мы шаг за шагом решили пример ниже.
Пример расчета средней скорости изменения функции
- Рассчитаем среднюю скорость изменения на интервале [2.5] следующей функции:
![]()
Сначала вычисляем значение функции при x=2 и x=5:
![]()
![]()
А затем вычисляем среднюю скорость изменения функции на интервале, просто применив формулу:
![]()
![]()
Поскольку результат TVM[2,5] положителен, это означает, что функция растет в интервале [2,5]. С другой стороны, если бы результат был отрицательным, это означало бы, что функция убывает на этом интервале.
Геометрическая интерпретация средней скорости изменения
Геометрически средняя скорость изменения функции на интервале представляет собой наклон линии, соединяющей крайние точки интервала.
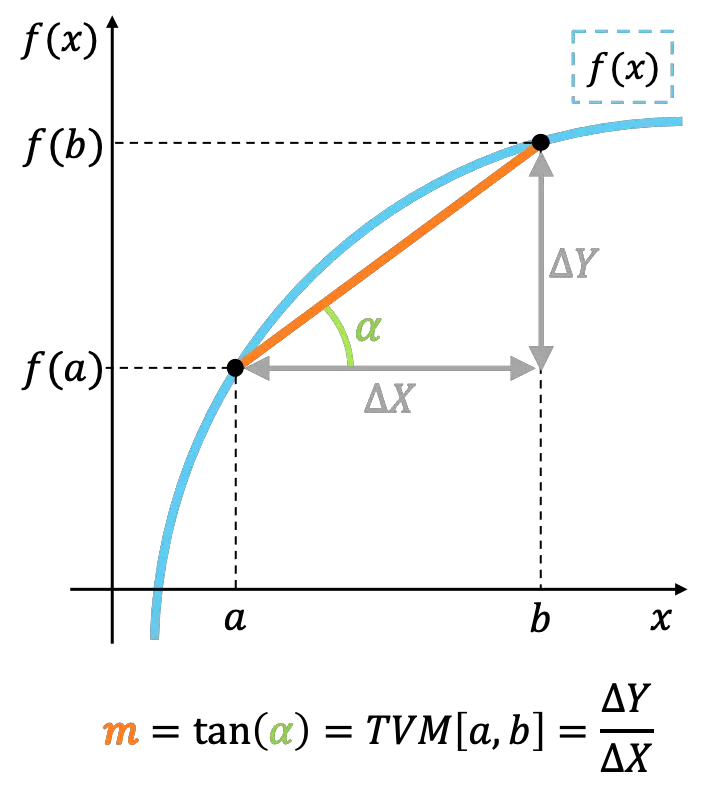
Мгновенная скорость изменения
Мгновенная скорость изменения (TVI) функции в точке — это бесконечно малый предел относительного увеличения функции на интервале. Следовательно, мгновенная скорость изменения вычисляется путем решения предела частного f(a+h)-f(a) при условии , что h приближается к нулю.
![]()
Значение мгновенной скорости изменения может быть положительным, отрицательным или нулевым и означает, что функция в этой точке увеличивается, уменьшается или остается неизменной соответственно в этой точке.
Пример расчета мгновенной скорости изменения функции
- Рассчитайте мгновенную скорость изменения в точке x=2 следующей функции:
![]()
Чтобы рассчитать мгновенную скорость изменения, нам нужно применить формулу:
![]()
![]()
Разрешаем примечательную идентичность:
![]()
➤ Если вы уже не помните формулы для примечательных тождеств , все формулы вы найдете на нашем сайте, специализирующемся на полиномах: www.polinomios.org
Теперь попробуем решить предел:
![]()
Но мы находим нулевую неопределенность между нулем, поэтому:
![]()
➤ См.: как решить предел с нулевой неопределенностью между нулем
И, наконец, решаем предел:
![]()
Еще:
![]()
Поскольку результат TVI(2) положительный, это означает, что функция возрастает при x=2. С другой стороны, если бы результат был отрицательным, это означало бы, что функция на данном этапе убывает.
Геометрическая интерпретация мгновенной скорости изменения
Геометрически мгновенная скорость изменения функции в точке представляет собой наклон линии, касательной к функции в этой же точке.
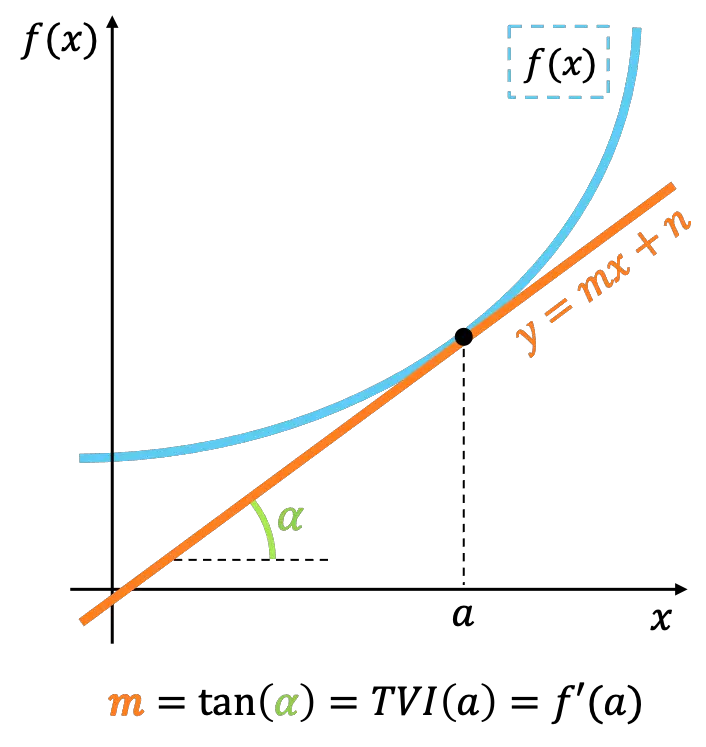
Если присмотреться, значение мгновенной скорости изменения эквивалентно понятию производной функции . Таким образом, мгновенная скорость изменения также используется для расчета значения производной функции в точке.
Решенные упражнения на скорость изменения
Упражнение 1
Вычислите значение скорости изменения следующей функции на интервале [1,3].
![]()
Сначала определим значение функции на концах отрезка:
![]()
![]()
А теперь применим формулу скорости изменения:
![]()
![]()
Упражнение 2
Рассчитайте среднюю скорость изменения (TVM) следующей функции на интервале [1,4]:
![]()
Сначала мы вычисляем изображения функции в точках x=1 и x=4.
![]()
![]()
И применим формулу средней скорости изменения:
![]()
![]()
Упражнение 3
Найдите среднюю скорость изменения следующей функции на интервале [-1,3]:
![]()
Чтобы определить среднюю скорость изменения, нам сначала нужно вычислить f(-1) и f(3):
![]()
![]()
Теперь воспользуемся формулой средней скорости изменения:
![]()
![]()
Упражнение 4
Рассчитайте среднюю скорость изменения в интервале [2,4] функции, показанной на следующем графике:

Применим формулу средней скорости изменения:
![]()
![]()
Как видно из формулы, нам нужно найти значение f(4) и f(2). И это легко сделать, взглянув на графическое представление функции:
![]()
![]()
И теперь, когда мы знаем значения функции, подставляем их в формулу:
![]()
Упражнение 5
Рассчитайте мгновенную скорость изменения следующей функции в точке x=2:
![]()
Для определения мгновенной скорости изменения функции в точке x=2 применим соответствующую ей формулу:
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73ee822823f921f75014cb9b50e47f51_l3.png)
Упражнение 6
Определите мгновенную скорость изменения (TVI) следующей функции в точке x=1:
![]()
Применим формулу мгновенной скорости изменения:
![]()
![]()
Затем мы вычисляем
![]()
И
![]()
![]()
![]()
И подставляем найденные значения в пределе:
![]()
Решаем примечательный продукт:
![]()
Теперь попробуем решить предел:
![]()
Но мы находим неопределенную форму ноль, разделенную на ноль, поэтому факторизуем многочлен числителя дроби и упрощаем:
![]()
➤ Если вы не знаете , как решить нулевую неопределенность между нулем , вы можете увидеть полное объяснение по ссылке выше о том , как решить предел с нулевой неопределенностью между нулем.
И, наконец, мы разрешаем предел:
![]()
Таким образом, мгновенная скорость изменения функции в точке x=1 равна 2.
![]()
Упражнение 7
Найдите мгновенную скорость изменения следующей функции в точке x=2:
![]()
Сначала мы используем формулу мгновенной скорости изменения:
![]()
![]()
Мы рассчитываем
![]()
И
![]()
![]()
![]()
И подставляем найденные значения в пределе:
![Rendered by QuickLaTeX.com \text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ad59f5f751af139656a471bf2a41801_l3.png)
Вычислим примечательное равенство:
![]()
Оперируем числителем:
![]()
Теперь попробуем решить предел:
![]()
Но мы получаем ноль неопределенности, разделенный на ноль, поэтому факторизуем многочлены и упрощаем:
![]()
И, наконец, мы разрешаем предел:
![]()
Еще:
![]()