▷ Что такое и как вычисляется комбинаторное число (примеры)

На этой странице мы объясняем, что такое комбинаторное число и как оно рассчитывается (формула). Кроме того, вы сможете увидеть примеры расчета любого комбинаторного числа и потренироваться на пошагово решаемых упражнениях. Также мы показываем все свойства и применения комбинаторных чисел. И, наконец, мы научимся находить результат комбинаторного числа непосредственно с помощью калькулятора.

Что такое комбинаторное число?

В математике комбинаторное число , также называемое биномиальным коэффициентом, — это количество обычных комбинаций (сочетаний без повторения) групп из k элементов, которые можно образовать из набора из n элементов (n>k).

Комбинаторное число выражается в скобках следующим образом:

$\begin{pmatrix}n \\ k \end{pmatrix}$

С другой стороны, комбинаторное число читается n по k . Точно так же n называется числителем, а k — порядком.

Просто имея определение комбинаторного числа, сложно понять его смысл. Однако сейчас мы увидим, как комбинаторное число определяется математически, а затем углубимся в это понятие комбинаторики. Вы увидите, что так вы поймете это лучше.

Формула комбинаторного числа

Формула расчета значения комбинаторного числа (или биномиального коэффициента) выглядит следующим образом:

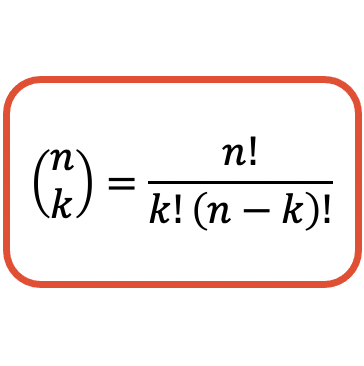
Помните, что в алгебре восклицательный знак соответствует факториалу числа. А чтобы найти факториал числа, вам нужно умножить все положительные целые числа, равные 1, на это число. Например, чтобы вычислить факториал числа 4, необходимо умножить 1, 2, 3 и 4:

$4! = 1\cdot 2 \cdot 3 \cdot 4 =24$

Также важно знать, что факториал 0 равен 1.

$0! = 1$

Пример вычисления комбинаторного числа

Далее мы пошагово определим значение комбинаторного числа на примере, чтобы вы могли увидеть, как это делается:

Вычислите значение комбинаторного числа 5 над 3.

Биномиальный коэффициент 5 к 3 соответствует следующему выражению:

$\begin{pmatrix}5 \\ 3 \end{pmatrix}$

Следовательно, если применить формулу комбинаторных чисел, для определения ее значения необходимо выполнить следующие операции:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}$

Или эквивалент:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}$

Итак, находим факториалы:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}$

Умножение 1·2·3 повторяется в числителе и знаменателе, поэтому дробь можно упростить, исключив этот множитель:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}$

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}$

Теперь посчитаем продукты:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}$

И наконец, делаем разделение:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}$

Свойства комбинаторного числа

Комбинаторные числа, или биномиальные коэффициенты, можно комбинировать по следующим свойствам:

Два дополнительных комбинаторных числа — это те, которые имеют одинаковый числитель n и сумма их порядков эквивалентна указанному числителю. Таким образом, результат двух дополнительных комбинаторных чисел идентичен.

$\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}$

Эту характеристику комбинаторных чисел еще называют тождеством симметрии.

Например, 6 больше 4 дает тот же результат, что и 6 больше 2, потому что 6-4 = 2.

$\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}$

$\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}$

Сумма двух комбинаторных чисел с одинаковым числителем и последовательными порядками равна другому комбинаторному числу, числитель которого эквивалентен числителю сложения плюс 1 и порядок которого соответствует наибольшему значению порядков сложения. Другими словами, всегда выполняется следующее условие:

$\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}$

Например:

$\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}$

Это свойство также известно как правило Паскаля.

С другой стороны, эту формулу можно применить и в обратном порядке, чтобы разложить комбинаторное число на два более простых комбинаторных числа:

$\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}$

Например, комбинаторное число 8 над 4 равно 7 над 3 плюс 7 над 4:

$\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}$

Любое положительное число больше 1 равно самому числу.

$\begin{pmatrix}n\\ 1 \end{pmatrix} =n$

Причиной этого свойства является то, что факториал числа равен факториалу предыдущего числа, умноженному на само число:

$\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n$

Примеры комбинаторных чисел этого типа:

$\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9$

Любое положительное число больше 0 равно единице.

$\begin{pmatrix}n\\ 0 \end{pmatrix} =1$

Действительно, знаменатель дроби такого комбинаторного числа всегда будет равен числителю дроби:

$\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1$

Примеры таких комбинаторных чисел:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1$

Каждое число само по себе равно 1.

$\begin{pmatrix}n\\ n \end{pmatrix} =1$

Вот демо:

$\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1$

Примеры таких комбинаторных чисел:

$\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1$

Как посчитать комбинаторное число с помощью калькулятора

До сих пор мы видели, как найти комбинаторное число из более или менее простых чисел, но когда нам приходится оперировать очень большими величинами, для определения комбинаторного числа лучше воспользоваться калькулятором. Теперь мы увидим, как ввести комбинаторное число в калькулятор.

Итак, ключ, используемый для вычисления комбинаторного числа с помощью калькулятора, — это ключ nCr . А чтобы определить значение комбинаторного числа, необходимо сначала ввести числитель комбинаторного числа, во-вторых нажать клавишу nCr, затем ввести порядок комбинаторного числа и, наконец, нажать клавишу равенства.

$\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}$

В научных калькуляторах CASIO клавиша nCr обычно имеет собственную кнопку или находится над кнопкой деления, в зависимости от модели.

Например, если мы хотим узнать, каково комбинаторное число 10 и 6, мы должны выполнить следующую последовательность:

$\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210$

Применение комбинаторного числа

Если вы зашли так далеко, вы, вероятно, уже прекрасно знаете, как решить любое комбинаторное число. Но… для чего используется комбинаторное число? Что ж, тогда мы увидим все преимущества, которые дает этот тип совершенно специальной операции.

Комбинаторика

Как мы видели вверху страницы, результат комбинаторного числа

$\begin{pmatrix}n\\ k \end{pmatrix}$

представляет собой количество возможных групп

$k$

элементы, которые могут быть сформированы из совокупности совокупности

$n$

предметы.

Следовательно, некоторые комбинаторные задачи можно решить, используя комбинаторные числа (или биномиальные коэффициенты). Давайте посмотрим, как это сделать на примере:

В классе из 30 учеников мы хотим выбрать группу из 4 учеников для выполнения определенных задач. Какое общее количество различных групп можно образовать?

При этом порядок следования учащихся не имеет значения, один и тот же ученик не повторяется дважды внутри группы и не все ученики входят в группу. Следовательно, формулу комбинаторного числа можно использовать для определения сколькими способами можно сформировать группу.

Для этого необходимо вычислить комбинаторное число, в котором в числителе указано общее количество учащихся, а в качестве порядка — количество учащихся, которые составят группу:

$\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}$

Таким образом, общее количество возможных комбинаций составляет 27 405 групп.

Бином Ньютона

Другое применение комбинаторных чисел — бином Ньютона. Бином Ньютона — это многочлен, состоящий из двух членов, возведенных вместе в целое число, то есть бином Ньютона — это тот многочлен, который отвечает следующему алгебраическому выражению:

$(a+b)^n$

Очевидно, что если бином возведен в квадрат, это означает, что он является заметным тождеством и, следовательно, его можно легко вычислить по соответствующей формуле. С другой стороны, когда бином возводится в большие числа, расчет становится весьма затруднительным. Что ж, биномиальная теорема Ньютона гласит, что эти типы многочленов можно очень легко вычислить из комбинаторных чисел.

Нажмите на следующую ссылку и узнайте, что такое биномиальная формула Ньютона и как она рассчитывается. Кроме того, вы сможете увидеть примеры и попрактиковаться в упражнениях, решаемых шаг за шагом. И, наконец, вы узнаете любопытную историю этой теоремы.

Треугольник Тартальи (или Паскаля)

Как вы видели в этой статье, вычисление биномиального коэффициента больших чисел вручную может быть трудоемким и сложным.

С другой стороны, с помощью треугольника Тартальи, также называемого треугольником Паскаля, все комбинаторные числа можно легко определить с помощью мнемонического правила. Логически это очень полезно, поскольку экономит много времени при расчетах.

Чтобы узнать, как именно это сделать, см. объяснение треугольника Тартальи . На этой связанной странице вы узнаете, что это за загадочный треугольник, для чего он используется (у него есть удивительные применения) 😮 и каково его происхождение (его использовали уже более 1000 лет назад).

Решаемые упражнения на комбинаторные числа

Чтобы вы могли попрактиковаться и полностью понять изложенные концепции, мы оставляем вам несколько упражнений, решаемых шаг за шагом по комбинаторным числам.

Упражнение 1

Найдите комбинаторное число 9 по 5 (не используя калькулятор).

Посмотреть решение

Чтобы найти значение комбинаторного числа 9 из 5, мы просто применяем формулу факториала:

$\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}$

Упражнение 2

Каков результат следующей суммы двух комбинаторных чисел? (без калькулятора)

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}$

Посмотреть решение

Из свойств комбинаторных чисел следует, что сумма задачи равна следующему комбинаторному числу:

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}$

Поэтому достаточно вычислить комбинаторное число 11 из 7:

$\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}$

Упражнение 3

Определите, равны ли следующие комбинаторные числа:

$\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}$

Посмотреть решение

Чтобы найти результат трех комбинаторных чисел, вам не нужно использовать калькулятор, но их можно легко найти благодаря свойствам комбинаторных чисел.

Прежде всего, комбинаторное число любого числа, большего 0, дает 1. Следовательно:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1$

С другой стороны, любое число больше единицы равно самому числу. Еще:

$\begin{pmatrix}6\\ 1 \end{pmatrix} =6$

И, наконец, любое комбинаторное число, образованное дважды повторенным одним и тем же числом, эквивалентно 1. Итак:

$\begin{pmatrix}6\\ 6 \end{pmatrix} =1$

В заключение отметим, что первое и третье комбинаторные числа в задаче равны, однако они отличаются от среднего комбинаторного числа.

$\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}$

Комбинаторное число (или биномиальный коэффициент)

Что такое комбинаторное число?

Формула комбинаторного числа

Пример вычисления комбинаторного числа

Свойства комбинаторного числа

Как посчитать комбинаторное число с помощью калькулятора

Применение комбинаторного числа

Комбинаторика

Бином Ньютона

Треугольник Тартальи (или Паскаля)

Решаемые упражнения на комбинаторные числа

Упражнение 1

Упражнение 2

Упражнение 3

Оставьте комментарий Отменить ответ