Здесь мы объясняем, как вывести степень (или потенциальную функцию), вы найдете формулу для производной степени, несколько примеров и даже можете попрактиковаться, выполняя упражнения, решаемые шаг за шагом.
Формула производной степени
Производная степени, или потенциальная функция, представляет собой произведение показателя степени на возведенное в показатель степени основание минус 1 умноженное на производную основания.
![]()
Следовательно, если основанием является тождественная функция , чтобы получить степень, просто умножьте функцию на показатель степени и вычтите из показателя степени одну единицу:
![]()
Действительно, производная тождественной функции равна 1.
Таким образом, для получения потенциальной функции есть две формулы: первую, которую можно использовать всегда, и вторую, которую можно применять только в том случае, если основанием является x.
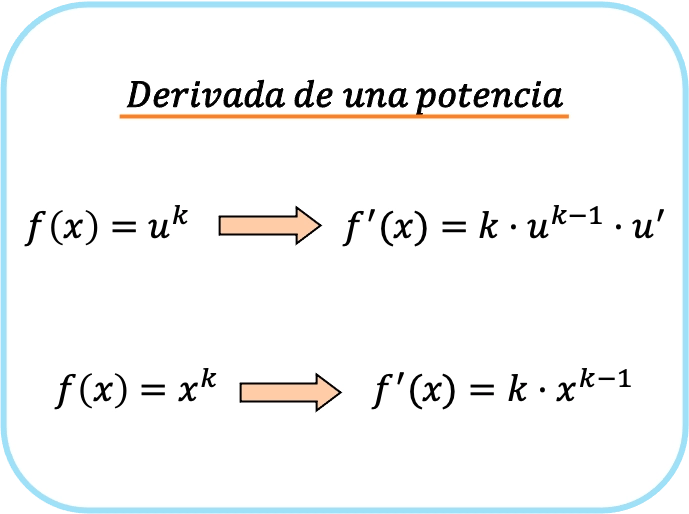
Мы можем легко проверить, что первая формула, представленная для производной степени, аналогична второй, но с применением правила цепочки.
Обратите внимание, что эти формулы можно использовать только в том случае, если переменная является основанием степени. Если x находится в знаменателе, вы должны применить правило для производной показательной функции:
➤ См.: производная показательной функции
Примеры степенных производных
После того, как мы увидели формулу производной потенциальной функции, мы объясним несколько примеров производной этого типа, чтобы вы поняли, как выводятся степени.
Пример 1: Производная базовой мощности x
![]()
Как мы объяснили в предыдущем разделе, когда основанием степени является только x, формула, которую мы должны использовать для получения функции:
![]()
Таким образом, производная степени x, возведенной в степень 4, равна:
![]()
Пример 2: Производная степени с круглыми скобками
![]()
В этом примере основание не является тождественной функцией, поэтому мы должны использовать общую формулу для производной степени:
![]()
Функция в скобках является линейной функцией, поэтому ее производная равна 2. Следовательно, производная всей потенциальной функции равна:
![]()
Пример 3: Производная отрицательной степени
![]()
В этом случае у нас есть потенциальная функция, показатель которой отрицательный, а основанием является логарифм, поэтому мы будем использовать следующую формулу для дифференцирования функции:
![]()
Даже если показатель степени отрицательный, из него тоже нужно вычесть. Таким образом, производная функции равна:
![]()
Если у вас есть какие-либо сомнения относительно решения, вы можете ознакомиться с формулой производной логарифмической функции здесь:
➤ См.: производная логарифмической функции.
Пример 4: Производная степени с корнем
![]()
Функция в этом примере представляет собой степень в регулярном выражении. Однако радикалы можно преобразовать в потенциальные выражения, поэтому функцию можно упростить, превратив ее в потенциальную функцию с дробным показателем:
![]()
Теперь применим формулу производной степени переменной:
![]()
И производная:
![]()
Вы также можете различать эти типы функций, используя правило корневой производной:
➤ См.: производное от корня
Решенные упражнения на производную степени
Вычислите производную следующих степеней:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
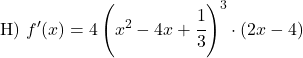
![]()