В этой статье мы объясним, как вывести вычитание функций (формулу). Вы также найдете примеры производных на вычитание и решенные пошаговые упражнения для практики.
Формула производной от вычитания
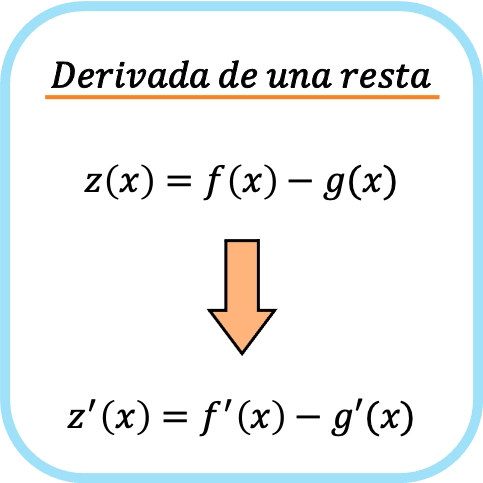
Производная от вычитания двух функций равна вычитанию производной каждой функции в отдельности.
![]()
Другими словами, дифференцирование двух функций по отдельности, а затем их вычитание эквивалентно сначала вычитанию функций, а затем взятию производной.
Аналогично, то же правило дифференцирования применимо к вычитанию двух или более функций, поэтому, если у нас есть вычитание трех, четырех, пяти… функций, нам нужно продифференцировать каждую отдельно, а затем вычесть их.
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bc282473a7f7560eebc97db66bb8f54_l3.png)
Как видите, формула производной разности функций очень похожа на правило производной суммы.
➤ См.: производная суммы функций
Примеры производной вычитания
Разобравшись с формулой производной вычитания, мы перейдем к анализу нескольких примеров производных этого типа операций, чтобы полностью понять, как выводятся вычитания функций.
Пример 1: Производная от вычитания потенциальных функций
![]()
Производная от вычитания двух функций эквивалентна разности производных каждой функции в отдельности. Поэтому сначала вычислим производную каждой функции отдельно:
![]()
![]()
Таким образом, производная всей функции равна:
![]()
Пример 2: Производная от вычитания различных функций
![]()
Чтобы дифференцировать функции вычитания, необходимо сначала дифференцировать две функции отдельно, а затем вычесть их.
![]()
![]()
И сделав две производные, вычитаем их в том же начальном порядке:
![]()
Пример 3: Производная квадрата вычитания
![]()
В данном случае у нас есть составная функция, поскольку она представляет собой вычитание между тремя квадратами функций. Поэтому мы должны использовать формулу производной потенциальной функции и цепное правило для вычисления производной всей функции:
![]()
➤ См.: формула производной степени
Решенные упражнения на производную от вычитания
Выполните следующие вычитания функций:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Доказательство производной вычитания
Далее мы продемонстрируем формулу производной от вычитания функции из определения производной, которая есть:
![]()
Итак, если z — это разница двух разных функций:
![]()
![]()
Заменим z вычитанием функций в предельном выражении:
![]()
![]()
Теперь сделаем преобразование, чтобы разделить дробь и получить вычитание двух дробей:
![]()
![]()
Применяя законы пределов, мы можем разделить приведенное выше выражение на два разных предела. Потому что предел вычитания равен вычитанию пределов:
![]()
Если присмотреться, каждому пределу соответствует производная функции, а значит, удовлетворяется формула производной разности:
![]()