В этой статье мы увидим, как найти котангенс функции. Вы найдете примеры производной котангенса и даже упражнения, решаемые шаг за шагом. Наконец, докажем формулу для производной котангенса.
Формула производной котангенса
Производная котангенса x равна отрицательной единице по квадрату синуса x. Производная котангенса x также равна минус квадрату косеканса x и минус сумме единицы плюс квадрат котангенса x.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a3653f5c765d773ebc789107bf1a825_l3.png)
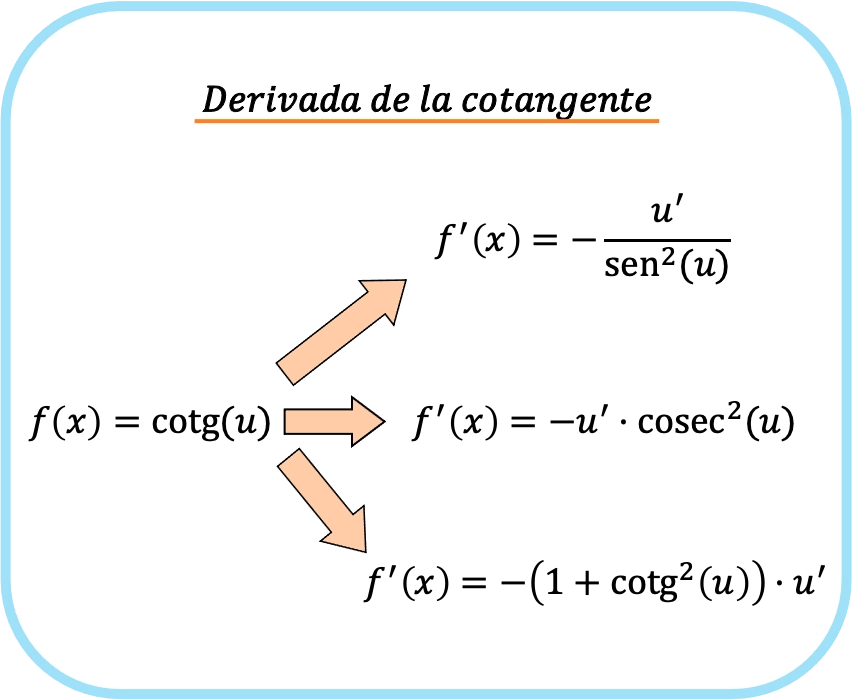
Если котангенс аргумента является функцией, отличной от x, формулы для производной котангенса функции такие же, как и предыдущие, но с умножением выражений на производную функции аргумента.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38ea1d1edeaf5664c56a946b5a87577d_l3.png)
Это означает, что существуют три разные формулы для нахождения производной котангенса. Но, по логике вещей, необязательно использовать все три формулы, а можно вывести по той формуле, которая вам больше нравится.
Примеры производной котангенса
Теперь, когда мы увидели формулу производной котангенса функции, в этом разделе мы решим несколько примеров тригонометрических производных этого типа.
Пример 1: Производная котангенса 2x
В этом примере мы увидим, чему равна производная котангенса функции 2x.
![]()
Как мы видели, для расчета производной котангенса можно использовать одну из трех формул, представленных выше. В данном случае воспользуемся формулой синусоиды:
![]()
Поскольку 2x является членом первой степени, его производная равна 2. Таким образом, производная котангенса 2x равна минус двум, разделенным на квадрат синуса 2x:
![]()
Пример 2: Производная котангенса x в квадрате
Во втором примере мы определим, чему равна производная котангенса x в квадрате.
![]()
В этом примере функция аргумента котангенса не является x, поэтому мы должны применить правило цепочки, чтобы дифференцировать котангенс.
![]()
Производная x в квадрате равна 2x, поэтому производная котангенса x 2 равна:
![]()
Пример 3: Производная котангенса в кубе
Наконец, найдем, чему равна производная куба котангенса полиномиальной функции:
![]()
В данном случае мы имеем композицию функций, поэтому нам нужно использовать цепное правило с формулой производной степени, чтобы найти производную котангенса:
![]()
Решенные упражнения на производную котангенса
Вычислите производную следующих котангенсов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
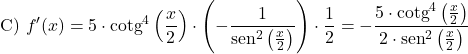
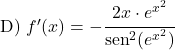
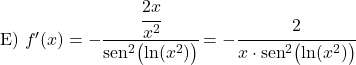
Доказательство производной котангенса
В этом последнем разделе мы продемонстрируем формулу производной котангенса. Для этого начнем с математического определения котангенса, который равен косинусу, разделенному на синус:
![]()
Теперь дифференцируем функцию, применив правило для производной частного;
![]()
![]()
![]()
Берем общий множитель в знаменателе и убираем отрицательный знак из дроби:
![]()
![]()
С другой стороны, мы знаем, что квадрат синуса плюс квадрат косинуса равен единице благодаря фундаментальному тригонометрическому тождеству.
![]()
![]()
И мы таким образом получили первую формулу для производной котангенса. Аналогично, косеканс является мультипликативной инверсией синуса, поэтому второе правило производной котангенса также доказано:
![]()
Наконец, третью формулу производной этой тригонометрической функции можно доказать, превратив дробь из предыдущего шага в сумму дробей:
![]()
![]()
![]()