В этой статье мы объясним, как получить гиперболический косеканс функции. Кроме того, вы сможете увидеть несколько решенных примеров производной гиперболического косеканса.
Формула производной гиперболического косеканса
Производная гиперболического косеканса x равна минус гиперболическому косекансу x, умноженному на гиперболический котангенс x.
![]()
Следовательно, производная гиперболического косеканса функции равна произведению гиперболического косеканса функции на гиперболический котангенс функции, умноженного на производную указанной функции.
![]()
Вкратце, формула для получения косеканса функции такова:
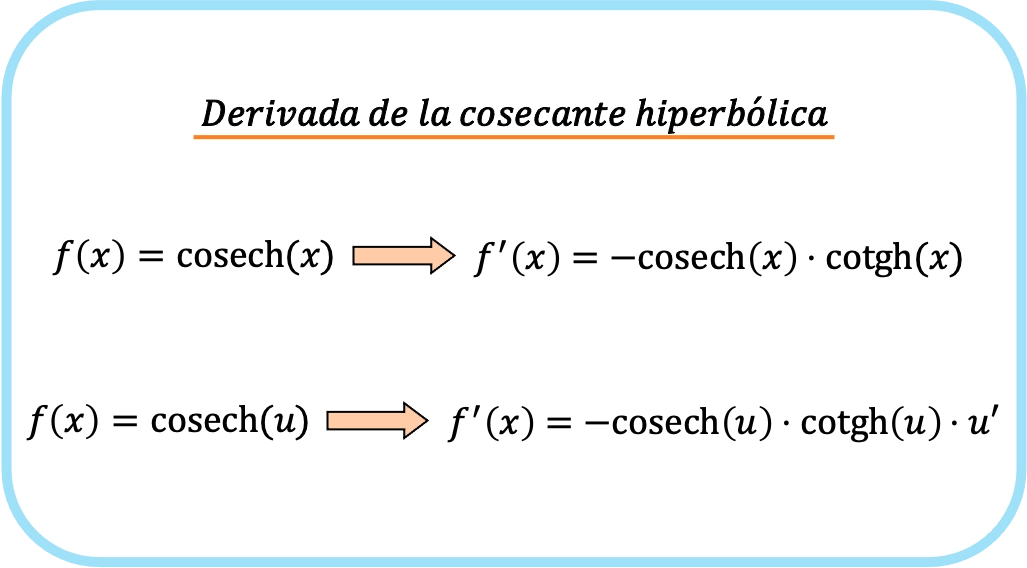
По сути, предыдущие два выражения соответствуют одной формуле, разница в том, что во второй формуле применяется правило цепочки.
Примеры производной гиперболического косеканса
Увидев, какова формула производной гиперболического косеканса, вот несколько рабочих примеров этого типа тригонометрической производной.
Пример 1
В этом первом примере мы выведем гиперболический косеканс x в квадрате:
![]()
Функция аргумента гиперболического косеканса отличается от x, поэтому нам нужно использовать формулу производной гиперболического косеканса с цепным правилом.
![]()
Итак, чтобы вывести эту тригонометрическую функцию, нам просто нужно подставить значения в предыдущую формулу, то есть в аргументе гиперболического косеканса и гиперболического тангенса мы ставим x 2 , и умножаем все на производную x в квадрате, что равно 2x:
![]()
Пример 2
В этом упражнении мы увидим, какова величина производной гиперболического косеканса x в кубе:
![]()
Чтобы найти производную гиперболического косеканса функции, применим ее формулу:
![]()
Производная x в кубе равна 3x 2 , поэтому производная всей функции равна:
![]()