На этой странице объясняется, как умножить вектор на действительное число (или скаляр) численно и графически. Кроме того, вы также найдете примеры и решенные упражнения на произведение вектора на скаляр. Наконец, также объясняются свойства этого типа операций с векторами.
Как умножить вектор на действительное число?
Чтобы численно вычислить произведение вектора и числа (или скаляра), каждый компонент вектора необходимо умножить на число.
![]()
![]()
Таким образом, в результате умножения вектора на число получается новый вектор со следующими характеристиками:
- Результат произведения вектора на скаляр создает новый вектор с тем же направлением, что и исходный вектор.
- Кроме того, новый вектор будет иметь то же направление, если число положительное.
- Или оно будет иметь противоположное значение, если число отрицательное.
- Величина результирующего вектора эквивалентна величине исходного вектора, умноженной на скаляр.
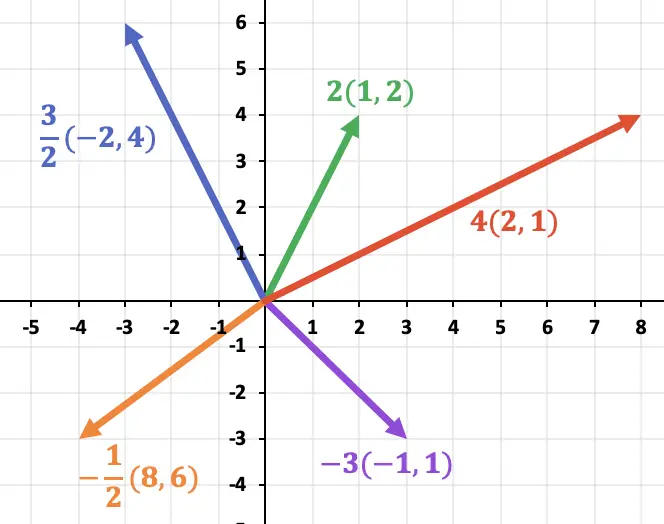
На следующем графике вы можете увидеть, как направление вектора сохраняется независимо от знака скаляра. С другой стороны, направление вектора зависит от знака числа, которое он умножает.

Кроме того, на следующем графике ясно видно, что величина результирующего вектора произведения равна величине исходного вектора, умноженного на скаляр.
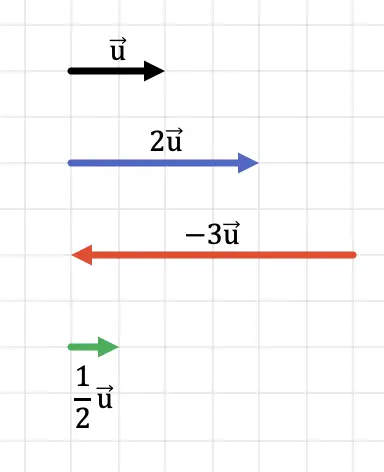
Очевидно, что если мы умножим вектор на число больше 1, в результате получится вектор большей длины (большего модуля). С другой стороны, если мы умножим вектор на число меньше 1, то в результате получится вектор меньшей длины (меньший модуль).
Примечание. Не путайте произведение вектора и скаляра со скалярным произведением векторов . Хотя у них похожее название, это два совершенно разных понятия.
Пример произведения вектора на скаляр
Далее мы увидим численный пример того, как вычисляется произведение вектора и числа:
- Умножьте следующий вектор на 4:
![]()
![]()
Как вы видели, этот тип векторной операции не очень сложен, поскольку вам не нужно выполнять много вычислений.
Однако существуют более сложные векторные операции, такие как сложение векторов и вычитание векторов. Если вы уже поняли, как вычислить произведение вектора и скаляра, рекомендуем перейти на следующий уровень и посмотреть, как решать сложение и вычитание векторов , так как это несколько более сложные операции и, по сути, они используются гораздо чаще (они более важны).
Свойства умножения вектора на число
Произведение вектора и числа обладает следующими свойствами:
- Ассоциативное свойство : когда вектор умножается более чем на одно число, порядок умножения не имеет значения.
![]()
- Распределительное свойство относительно сложения и вычитания векторов:
![]()
![]()
- Распределительное свойство относительно сложения скаляров:
![]()
- Нейтральный элемент : Очевидно, что любой вектор, умноженный на 1, дает сам вектор:
![]()
Решенные задачи умножения вектора на скаляр
Упражнение 1
Вычислите аналитически результат произведения следующего вектора на 3:
![]()
Чтобы найти произведение, необходимо каждую координату вектора умножить на 3:
![]()
Упражнение 2
Умножьте следующий вектор на 6 и найдите его модуль:
![]()
Сначала мы умножаем вектор на скаляр:
![]()
Теперь есть два способа вычислить величину полученного вектора. Первый — найти величину исходного вектора, а затем умножить ее на 6:
![]()
![]()
И второй способ — непосредственно вычислить величину вектора, полученного при умножении:
![]()
Таким образом, с помощью обеих процедур показано, что результат не зависит от метода расчета модуля.
Упражнение 3
Из следующего вектора:
![]()
Алгебраически вычислите следующие операции:
![]()
![]()
![]()
![]()
Затем определите, имеют ли полученные векторы то же направление и направление, что и исходный вектор, и упорядочите их от самого короткого к самому длинному.
Сначала посчитаем умножения:
![]()
![]()
![]()
![]()
Следовательно, векторы, умноженные на положительные числа, имеют то же направление и направление, что и исходный вектор. А векторы, умноженные на отрицательные числа, имеют то же направление, но противоположное направлению исходного вектора.
Векторы одного и того же направления:
![]()
И
![]()
Векторы одного направления, но разного значения:
![]()
Наконец, мы должны упорядочить векторы в соответствии с их длиной или, что то же самое, их модулем. Вектором наибольшей длины (или наибольшего модуля) будет тот, который был умножен на большее число (по абсолютному значению), а вектор наименьшей длины (или наименьший модуль) будет тот, который был умножен на меньшее число. число (в абсолютном значении). Итак, порядок длин следующий:
![]()
Обратите внимание, что длина или модуль не зависят от знака умножаемого скаляра, поскольку направление вектора не меняет его модуль.
Упражнение 4
Рассмотрим следующие два вектора:
![]()
Вычислите следующую операцию:
![]()
Сначала решаем умножение векторов на числа:
![]()
![]()
![]()
А затем вычитаем векторы:
![]()
![]()
Упражнение 5
Выполните следующие умножения векторов на скаляры и постройте график результатов:
![]()
![]()
![]()
![]()
![]()
Сначала мы умножаем векторы на действительные скаляры:
![]()
![]()
![]()
![]()
![]()
Наконец, после того, как мы вычислили векторы, мы представляем их на графике: