На этой странице мы объясняем, что такое смешанное произведение трех векторов (или тройное скалярное произведение) и как оно рассчитывается. Вы также увидите примеры, упражнения и решенные задачи по этому типу операций между векторами. И, кроме того, вы узнаете о свойствах и применении смешанного продукта.
Что такое смешанное произведение трех векторов?
Смешанное произведение трех векторов, также называемое тройным скалярным произведением , представляет собой последовательное умножение трех векторов, включающее два разных типа операций: скалярное произведение и векторное произведение . Итак, комбинация двух векторных операций дает скаляр (действительное число).
Конкретно смешанное произведение состоит из вычисления векторного произведения двух векторов и последующего векторного умножения полученного результата на третий вектор. Написанное так может показаться очень сложным, но на самом деле это не так уж и много, посмотрите на формулу тройного скалярного произведения:
![]()
Как видно в его формуле, смешанное произведение трех векторов обозначается двумя квадратными скобками.
Как вычислить смешанное произведение трех векторов?
Формула тройного скалярного произведения — это та, которую мы только что видели в предыдущем разделе, однако она обычно не используется для определения смешанного произведения трех векторов, поскольку есть другой, более простой и быстрый способ:
Пусть любые 3 вектора будут:
![]()
Чтобы вычислить смешанное произведение трех векторов, просто решите определитель 3×3, образованный компонентами векторов:
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fed933d4d02bb5ca6f5bae06ea544d_l3.png)
Итак, вы можете увидеть пример того, как это рассчитывается , мы найдем смешанное произведение следующих трех векторов:
![]()
Для определения смешанного произведения построим определитель третьего порядка, расположив векторы в строках матрицы:
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5341b4a39b42c1284a4b0129b38b61a_l3.png)
А теперь нам просто нужно решить определитель матрицы, для этого можно использовать любой метод. В этом случае мы применим правило Сарруса (но это можно сделать и с помощью дополнений или кофакторов):
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df86565048cf897265878936f2294525_l3.png)
Чтобы показать, что эти две процедуры эквивалентны, мы вычислим смешанное произведение одних и тех же векторов посредством их определения:
![Rendered by QuickLaTeX.com \begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4d15d610ca9b4cb39e9f268cfb152ae_l3.png)
Мы рекомендуем вычислять смешанное произведение через определитель векторов, так как это быстрее и меньше шансов допустить ошибку. Но, как видите, результат один и тот же независимо от того, какой метод вы используете, поэтому используйте тот, который вам больше нравится. 👍
Геометрическая интерпретация смешанного продукта
Когда вы узнаете, как найти смешанное произведение трех векторов, у вас может возникнуть вопрос… а для чего нужно смешанное произведение? Что ж, в математике у него есть два основных применения: вычисление объема параллелепипеда и объема тетраэдра.
Объем параллелепипеда равен абсолютной величине смешанного произведения векторов, обозначающих три измерения геометрического поля.
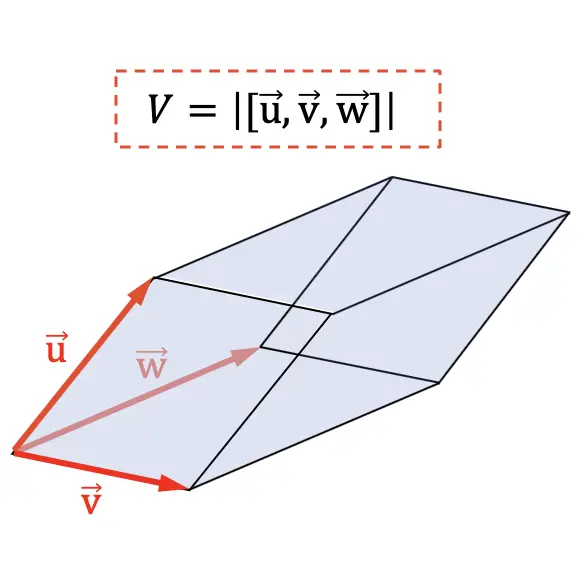
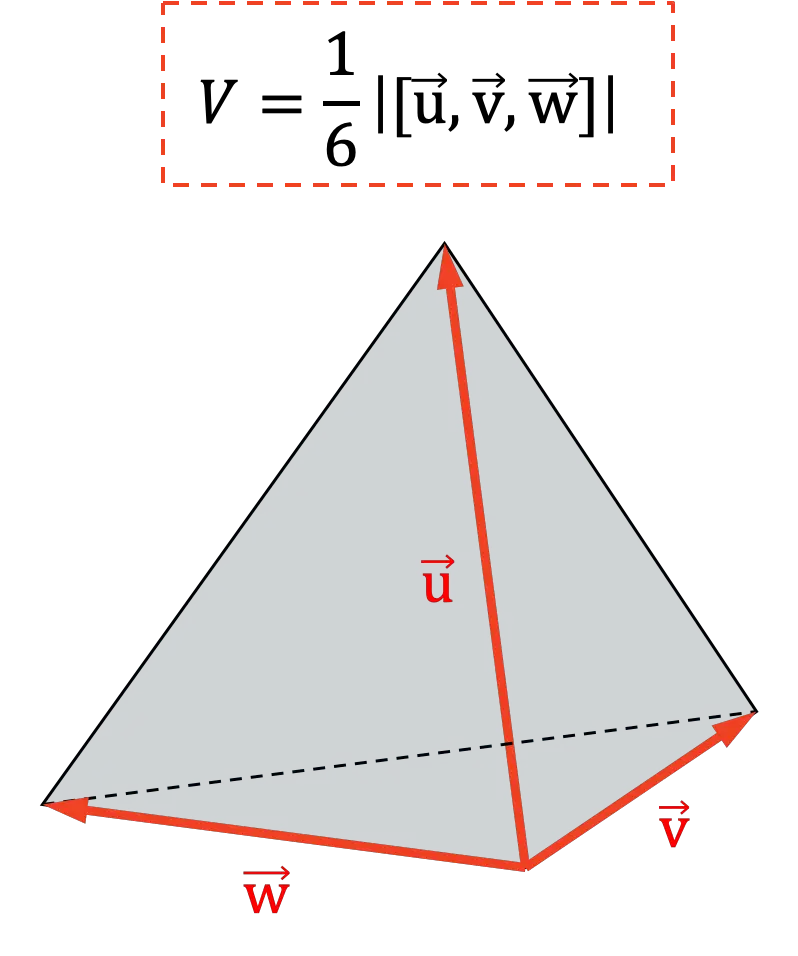
Другое применение смешанного произведения — определение объема тетраэдра . Поскольку геометрически шестая часть абсолютной величины смешанного произведения представляет собой объём тетраэдра:
Свойства смешанного произведения или тройного скалярного произведения
Смешанное произведение, или тройное скалярное произведение, имеет следующие характеристики:
- В общем случае изменение порядка векторов смешанного произведения также подразумевает изменение знака. Следовательно, порядок смешанных векторов произведений важен.
![]()
- Однако если циклически менять порядок, знак не изменится:
![]()
- В трехмерном пространстве (в R3) смешанное произведение трех линейно зависимых или компланарных векторов (принадлежащих одной плоскости) равно 0.
Исправлены проблемы со смешанными продуктами
Упражнение 1
Даны 3 вектора:
![]()
Вычислите смешанное произведение трех векторов:
![]()
Чтобы найти его смешанное произведение, надо решить определитель, составленный из координат векторов:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-549ed90889d541ae4a1075449567b062_l3.png)
Упражнение 2
Даны 3 вектора:
![]()
Определите смешанный продукт между тремя векторами:
![]()
Чтобы найти его смешанное произведение, нам нужно найти определитель, который имеет декартовы координаты векторов в линейной форме:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29b46155243552a99f6fd75de69f59da_l3.png)
Упражнение 3
Вычислите объем параллелепипеда, 3 стороны которого представляют собой следующие векторы:
![]()
Объем параллелепипеда равен абсолютной величине смешанного произведения трех векторов, которые у него есть ребра. Поэтому сначала вычисляем тройное векторное произведение векторов:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9718b369a508216fbb69ab68ac7de381_l3.png)
Так что объем параллелепипеда является абсолютной величиной результата смешанного произведения:
![]()
Упражнение 4
Вычислите объем тетраэдра, вершинами которого являются следующие точки:
![]()
Сначала вычислим векторы, представляющие ребра тетраэдра:
![]()
![]()
![]()
Объем тетраэдра эквивалентен одной шестой абсолютной величины смешанного произведения трех векторов, которые он имеет для ребер. Поэтому сначала вычисляем смешанное произведение найденных векторов:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d384e76415a756b834e0a8e7c695b1c1_l3.png)
Таким образом, объем тетраэдра будет составлять одну шестую абсолютной величины смешанного продукта:
![]()