Пересекающиеся линии

На этой странице вы найдете все о секущих линиях: что они означают, какие существуют типы, как узнать, являются ли две прямые секущими, как найти их общую точку… Вы также сможете увидеть несколько примеров и решенных упражнений. секущих линий.

Что такое две пересекающиеся прямые?

В математике определение секущих линий следующее:

Две прямые пересекаются, когда они пересекаются только в одной точке. Следовательно, пересекающиеся прямые имеют только одну общую точку. Более того, две пересекающиеся прямые обязательно должны находиться в одной декартовой плоскости.

Идея о том, что две линии, пересекающиеся в одной точке, важна, потому что, если бы у них было более одной точки пересечения, они были бы совпадающими линиями, а с другой стороны, если бы у них не было точки пересечения, они были бы параллельными линиями.

Примеры пересекающихся линий

После того, как мы поняли значение двух пересекающихся линий, давайте теперь посмотрим на 2 разных примера линий этого типа:

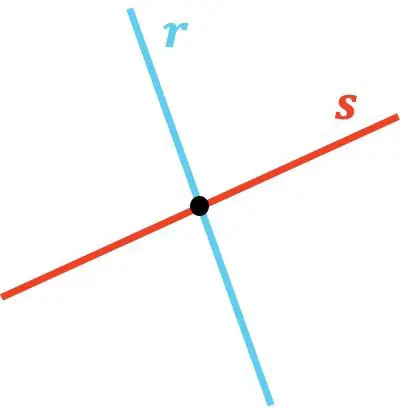
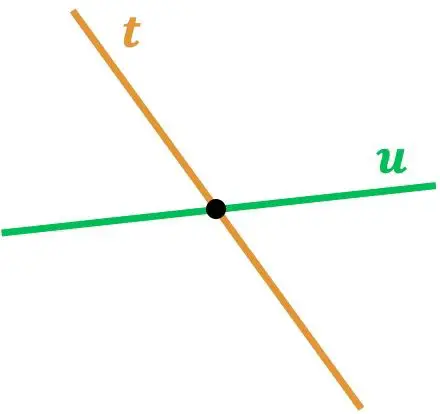
Как видите, линии r и s пересекаются, потому что соприкасаются в одной точке. И точно так же линия t пересекает линию u , поскольку существует точка их пересечения.

Виды пересекающихся линий

Существует два типа пересекающихся линий:

Перпендикулярные линии : линии, пересекающиеся под прямым углом 90°.
Косые линии: состоят из линий, пересекающихся под острым углом от 0° до 90° (не входят в комплект).

Перпендикулярные прямые

Перпендикулярные линии – это линии, которые пересекаются, образуя четыре угла по 90 градусов.

Аналогично, наклоны двух перпендикулярных прямых всегда удовлетворяют следующему условию:

$m_r = -\cfrac{1}{m_s}$

Еще одним свойством перпендикулярно пересекающихся линий является то, что скалярное произведение их векторов направления (вектор, указывающий направление линии) равно нулю.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

Если вас больше интересуют перпендикулярные линии, по этой ссылке вы можете увидеть примеры перпендикулярных линий . Кроме того, вы также узнаете, как рассчитать линию, перпендикулярную другой, свойства этого типа линии, пошагово решаемые упражнения и т. д.

косые линии

Косые линии — это линии, которые пересекаются, образуя попарно острые и тупые углы. То есть сделайте два острых угла (менее 90°) и два тупых угла (больше 90°). Однако, согласно определению угла двух линий, угол между двумя линиями является наименьшим из тех, которые он образует.

Угол между двумя косыми линиями с их наклонами можно рассчитать по следующей формуле:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Как узнать, что две прямые пересекаются?

В основном существует 3 метода определения взаимного положения двух линий:

С векторами направления двух линий.
Со склонами двух линий.
С неявным (или общим) уравнением двух линий.

Затем мы увидим объяснение трех методов, которые существуют, чтобы узнать, когда пересекаются две линии.

По векторам направления линий

Если координаты векторов направления (вектор, обозначающий направление линии) двух разных линий не пропорциональны , эти две линии пересекаются.

Давайте посмотрим, как поэтапно решается упражнение из двух пересекающихся линий:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

Обе линии выражаются в виде параметрических уравнений, поэтому компонентами вектора направления каждой линии являются числа перед параметром

$t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

Итак, чтобы увидеть, пропорциональны ли векторы направления, нам нужно разделить между ними координаты. Если мы получим одинаковый результат в обоих делениях, они будут пропорциональны; с другой стороны, если результат будет другим, это будет означать, что векторы не пропорциональны.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

Деления компонентов не равнозначны, поэтому векторы не пропорциональны и поэтому прямые пересекаются.

в начале склонов

Если две линии имеют разные наклоны , это означает, что линии пересекаются.

Например, следующие две линии пересекаются, поскольку они имеют разные наклоны:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

Наклон линии

$r$

равно -2 и наклон линии

$s$

это 3.

$m_r =-2 \neq m_s =3$

Поскольку две линии не имеют одинакового наклона, они пересекаются.

Из неявного уравнения линии

Также можно узнать, пересекаются ли две прямые или нет, с помощью неявных уравнений (или общих уравнений) линий. Неявное уравнение линии имеет следующий вид:

$Ax+By+C=0$

Таким образом, две прямые пересекаются, когда их коэффициенты A и B не пропорциональны.

Давайте посмотрим пример двух пересекающихся линий, определенных с помощью неявного уравнения:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

Чтобы убедиться, что это две пересекающиеся прямые, надо проанализировать пропорциональность коэффициента А (числа перед переменной

$x$

) с коэффициентом B (цифра перед переменной

$y$

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

Эти два члена не пропорциональны, поэтому две линии эффективно пересекаются.

Найдите общую точку двух пересекающихся прямых

Как мы видели, пересекающиеся прямые имеют только одну общую точку. Таким образом, чтобы вычислить точку пересечения двух секущих линий , необходимо решить систему уравнений, образованную двумя прямыми.

В качестве примера найдем точку пересечения следующих двух линий:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

Чтобы определить точку пересечения двух линий, мы должны решить систему линейных уравнений, образованную двумя линиями:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

В этом случае будем решать систему методом замены. Поэтому мы изолируем переменную

$x$

из первого уравнения и подставим его во второе уравнение:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

И как только мы узнаем, сколько стоит неизвестное

$y$

Подставим его значение в найденное выражение для

$x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

Таким образом, решением системы уравнений является точка пересечения двух линий. И этот момент

$\bm{(3,1)}.$

линия, пересекающая окружность

Обычно, когда мы говорим, что две линии пересекаются, мы имеем в виду только что увиденную концепцию. Однако в геометрии существует и другое значение секущей линии:

Линия, пересекающая окружность, — это линия, пересекающая окружность (или кривую) в двух разных точках.

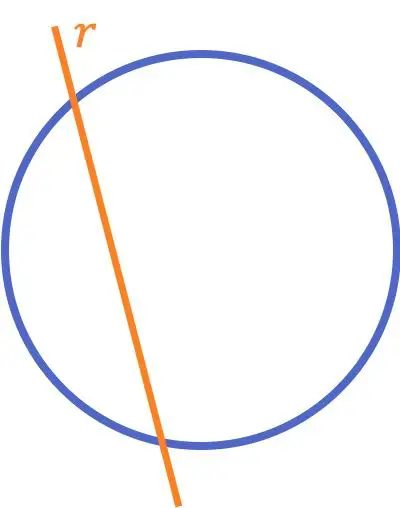
В отличие от понятия о двух пересекающихся линиях, которое обычно преподают в начальной школе, это определение линии, пересекающейся с кругом, часто изучается в более поздних классах вместе со всеми относительными положениями линий с кругами.