Антисимметричная матрица

На этой странице мы объясняем, что такое антисимметричные матрицы. Кроме того, вы сможете увидеть несколько примеров, а также его типичную структуру, чтобы лучше понять его. Также объяснены особенности вычисления определителя антисимметричной матрицы и все свойства этого типа матриц. И, наконец, вы узнаете, как разложить любую квадратную матрицу на сумму симметричной матрицы и другой антисимметричной матрицы.

Что такое антисимметричная матрица?

Определение антисимметричной матрицы следующее:

Антисимметричная матрица — это квадратная матрица, транспонирование которой равно отрицательному значению матрицы.

$A^t = -A$

Золото

$A^t$

представляет собой транспонированную матрицу

$A$

$-A$

это матрица

$A$

со всеми его элементами поменялся знак.

Примеры антисимметричных матриц

Как только мы узнаем концепцию антисимметричной матрицы, мы увидим несколько примеров антисимметричных матриц, чтобы лучше ее понять:

Пример антисимметричной матрицы порядка 2 × 2

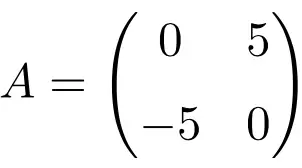
пример антисимметричной матрицы размерности 2x2

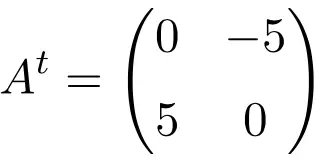
решено упражнение с антисимметричной матрицей размерности 2x2

Пример антисимметричной матрицы размерности 3×3

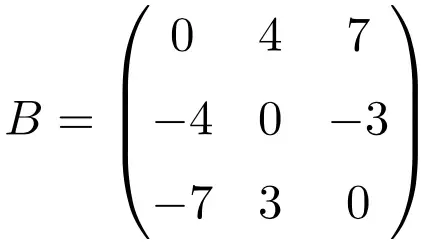
пример антисимметричной матрицы размером 3x3

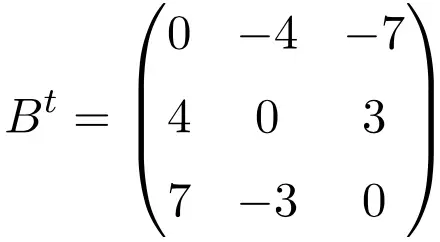
решено упражнение с антисимметричной матрицей размером 3x3

Пример антисимметричной матрицы размером 4×4

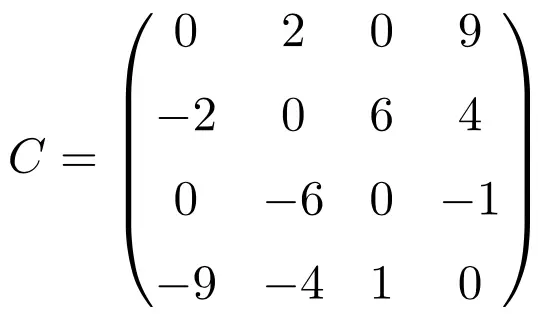
пример антисимметричной матрицы размерности 4х4

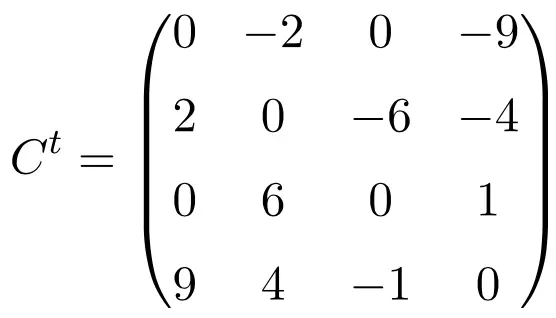
решено упражнение с антисимметричной матрицей размерности 4x4

Транспонируя эти три матрицы, мы проверяем, что они антисимметричны, поскольку транспонированные матрицы эквивалентны соответствующим исходным матрицам с измененным знаком.

Структура антисимметричной матрицы

Чтобы условие антисимметричности матрицы выполнялось, они всегда должны иметь один и тот же тип структуры: все числа на главной диагонали равны нулю, а элемент строки i и столбца j является отрицательным элементом элемента строки j и столбца. я . Другими словами, вид антисимметричных матриц следующий:

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

Следовательно, главная диагональ антисимметричной матрицы действует как ось антисимметрии. Отсюда и название этой конкретной матрицы.

Определитель антисимметричной матрицы

Определитель антисимметричной матрицы зависит от размерности указанной матрицы. Это обусловлено свойствами определителей:

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

Таким образом, если антисимметричная матрица нечетного порядка, ее определитель будет равен 0 . С другой стороны, если антисимметричная матрица четной размерности, определитель может принимать любое значение.

Следовательно, антисимметричная матрица нечетной размерности является сингулярной или вырожденной матрицей. С другой стороны, антисимметричная матрица четного порядка является регулярной матрицей.

Свойства антисимметричных матриц

Характеристики антисимметричных матриц следующие:

Сложение (или вычитание) двух антисимметричных матриц дает еще одну антисимметричную матрицу. Поскольку транспонирование двух добавленных (или вычтенных) матриц эквивалентно транспонированию каждой матрицы отдельно:

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

Любая антисимметричная матрица, умноженная на скаляр, также порождает другую антисимметричную матрицу.

Мощность антисимметричной матрицы эквивалентна антисимметричной матрице или симметричной матрице. Если показатель степени является четным числом, результат степени представляет собой симметричную матрицу, но если показатель степени является нечетным числом, результат степени представляет собой антисимметричную матрицу. По этой ссылке вы можете проконсультироваться , что такое симметричная матрица .

След антисимметричной матрицы всегда равен нулю.

Сумма любой антисимметричной матрицы плюс унитарная матрица дает обратимую матрицу.

$\displaystyle \text{det}(A+I)\neq 0$

Все действительные собственные значения (или собственные значения) антисимметричной матрицы равны 0. Однако антисимметричная матрица может иметь и комплексные собственные значения.

Все антисимметричные матрицы являются нормальными матрицами. Следовательно, на них распространяется действие спектральной теоремы, которая гласит, что антисимметричная матрица может быть диагонализирована унитарной матрицей.

Разложение квадратной матрицы на симметричную и антисимметричную матрицу

Особенностью квадратных матриц является то, что их можно разложить на сумму симметричной матрицы и антисимметричной матрицы.

Формула, которая позволяет нам это сделать, выглядит следующим образом:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Где C — квадратная матрица, которую мы хотим разложить, C ^— ее транспонировать, и, наконец, S и A — соответственно симметричная и антисимметричная матрицы, на которые разлагается матрица C.

Ниже вы найдете решенное упражнение, демонстрирующее формулу. Разложим следующую матрицу:

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

Рассчитаем симметричную и антисимметричную матрицу по формулам:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

И мы можем проверить, что уравнение выполняется, сложив две матрицы:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$

✅