На этой странице вы найдете объяснение правила (или закона) параллелограмма. Кроме того, вы увидите несколько примеров сложения и вычитания векторов с использованием правила параллелограмма, а также реальные приложения.
Что такое правило параллелограмма?
Как вы уже знаете, векторные величины нельзя складывать или вычитать так же, как действительные числа, поскольку они имеют 2 компоненты (в R2) или 3 компоненты (в R3) и потому что векторы могут иметь разные направления. Поэтому для выполнения векторных операций необходимы другие методы, например правило параллелограмма, которое состоит из следующего:
В математике правило параллелограмма — это процедура сложения или вычитания двух векторов из их графического представления.
Метод параллелограмма, безусловно, наиболее часто используется при сложении и вычитании векторов (графически), поскольку это очень простой в использовании метод. Например, в физике он используется для сложения и вычитания сил.
С другой стороны, правило немного меняется в зависимости от того, хотим ли мы складывать или вычитать векторы, поэтому ниже мы объясним обе версии отдельно.
Правило параллелограмма для сложения двух векторов
Если мы хотим сложить два вектора графически, шаги по применению правила или закона параллелограмма следующие:
- Сначала мы рисуем векторы и располагаем их в одной и той же точке приложения, то есть помещаем начала обоих векторов в одну и ту же точку.
- Затем мы рисуем в конце одного вектора линию, параллельную другому вектору. И повторяем шаг с другим вектором. Таким образом, мы получим рисунок параллелограмма (отсюда и название правила).
- Наконец, вектор, полученный в результате суммы, будет диагональю параллелограмма, идущей от общего начала векторов до точки пересечения двух параллельных прямых.
В следующем общем примере вы можете увидеть, как используется правило параллелограмма:

Если вы хотите попрактиковаться в использовании правила параллелограмма, по следующей ссылке вы можете ознакомиться с дополнительными примерами и несколькими решенными упражнениями на сложение векторов . На этой странице вы также найдете другие методы графического добавления векторов и даже способы их численного добавления.
Правило параллелограмма для вычитания двух векторов
Правило или метод параллелограмма также используется для вычитания двух векторов из графа. Итак, шаги для вычитания вектора:
- Сначала мы представляем два вектора на графике и располагаем их в одной и той же точке приложения, то есть помещаем начала обоих векторов в одну и ту же точку.
- Во-вторых, мы рисуем вектор, противоположный вектору, который вычитается в операции, или, другими словами, мы обращаем вектор, который вычитает.
- Затем мы рисуем линию, параллельную вектору смены знака, в конце вектора, сумма которого равна . И повторяем процесс с другим вектором. Так что у нас получится рисунок параллелограмма (отсюда и название правила).
- Наконец, результатом вычитания будет вектор, идущий от общего начала двух векторов до точки пересечения двух параллельных прямых.
Посмотрите на следующий общий пример, в котором два вектора вычитаются по закону параллелограмма:
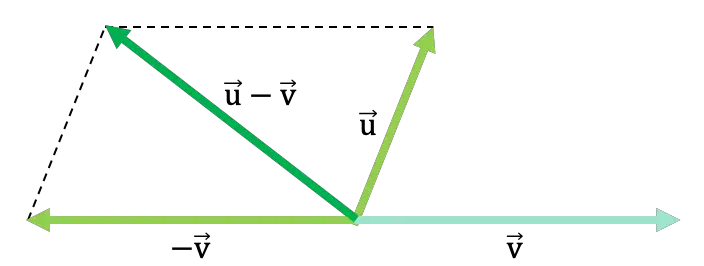
По следующей ссылке вы можете увидеть больше примеров вычитания векторов с помощью правила параллелограмма. Вы также можете попрактиковаться с решенными упражнениями на вычитание векторов . Кроме того, вы узнаете о других методах вычитания векторов из их графика и, наконец, о том, как они вычитаются численно.
Наконец, если объяснение этой техники было для вас полезным, вам наверняка также будет интересно узнать, что такое правило правой руки . На странице ссылки вы можете увидеть, что это такое, для какой векторной операции оно используется и какие существуют варианты этого правила.