Здесь вы узнаете, как решать все виды пределов на бесконечности: полиномиальные, рациональные, показательные функции, с корнями, неопределенности на бесконечности… Кроме того, вы сможете тренироваться с помощью 25 упражнений, решаемых шаг за шагом на пределах, когда x стремятся к бесконечности. .
Предел функции, когда x стремится к бесконечности
Предел функции при приближении x к бесконечности , положительный или отрицательный, может быть действительным значением, плюс бесконечность, минус бесконечность или отсутствовать. Чтобы найти пределы на бесконечности, вам нужно заменить x на бесконечность.
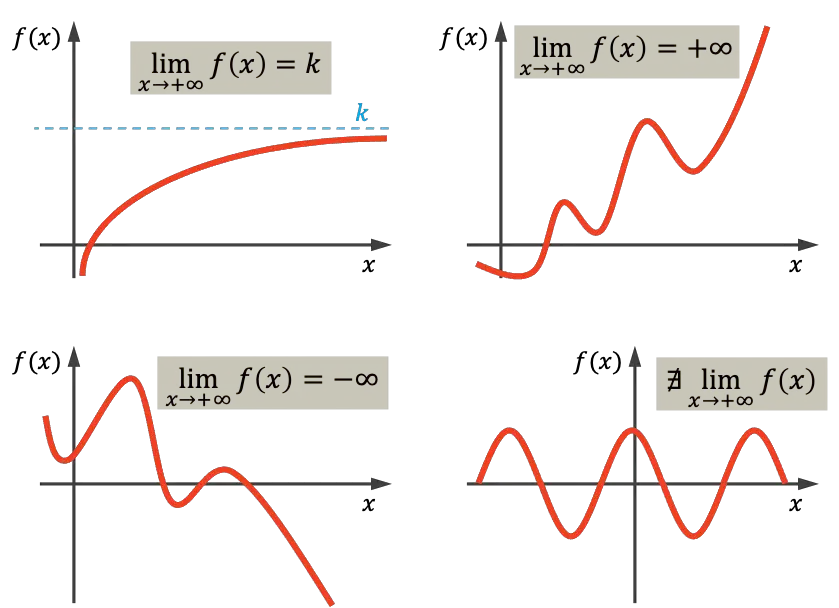
Как вы можете видеть на первом графике, показанная функция стремится к реальному значению k в направлении бесконечности, потому что она приближается к k по мере роста x . Функция в правом верхнем углу стремится к бесконечности по мере того, как x приближается к бесконечности, поскольку она неограниченно растет по мере увеличения значения x . С другой стороны, график слева внизу уменьшается без остановки и поэтому стремится к минус бесконечности. Наконец, последняя функция периодична и не стремится ни к какому значению, поэтому предела бесконечности в этом случае нет.
Как решить пределы на бесконечности
Чтобы решить предел до бесконечности в полиномиальных функциях, мы должны заменить x на бесконечность только в члене функции высшей степени.
Например, посмотрите на следующий расчет предела бесконечности, где мы подставляем только бесконечность в моном высшей степени:
![]()
Как вы можете видеть в примере, +∞ в квадрате дает +∞, поскольку очень большое число (+∞) в степени 2 всегда будет давать очень большое число (+∞).
И то же самое происходит с умножением: если вы умножите очень большое число (+∞), вы всегда получите очень большое число (+∞). Например:
![]()
Предупреждение: для расчета пределов до бесконечности важно учитывать следующие элементы:
→ Отрицательное число, возведенное в четную степень, является положительным. Следовательно, минус бесконечность, возведенная в четную степень, дает плюс бесконечность:
![]()
→ Отрицательное число, возведенное в нечетную степень, является отрицательным. Следовательно, минус бесконечность, возведенная в нечетную степень, равна минус бесконечности:
![]()
→ Умножение отрицательного числа меняет знак бесконечности:
![]()
→ Любое число, разделенное на
![]()
дает 0:
![]()
Примеры пределов до бесконечности
Итак, вы можете увидеть, как решаются пределы до бесконечности в полиномах. Ниже приведены несколько таких решений:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbab608d243555490569fab22938c6e9_l3.png)
Неопределенные пределы бесконечности
Пределы бесконечности не всегда будет так легко вычислить, поскольку иногда мы будем получать неопределенность бесконечности между бесконечностью или неопределенность бесконечности минус бесконечность.
![]()
Когда мы получаем этот тип неопределенностей (или неопределенных форм), мы не можем знать результат непосредственно, а скорее должны выполнить предварительную процедуру, чтобы найти предельное значение. Затем мы увидим, как разрешаются неопределенные пределы на бесконечности.
Бесконечная неопределенность между бесконечным
Чтобы найти результат неопределенности бесконечности, разделенной на бесконечность, мы должны сравнить степень числителя и степень знаменателя дроби:
- Если степень полинома числителя меньше степени полинома знаменателя, бесконечная неопределенность на бесконечности равна нулю.
- Если степень многочлена числителя эквивалентна степени многочлена знаменателя, бесконечная неопределенность на бесконечности представляет собой частное главных коэффициентов двух многочленов.
- Если степень многочлена числителя больше степени многочлена знаменателя, бесконечная неопределенность между бесконечностью дает большую или меньшую бесконечность (знак зависит от основных членов двух многочленов).
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.» title=»Rendered by QuickLaTeX.com» height=»139″ width=»767″ style=»vertical-align: 0px;»></p>
</p>
<p> Например, в следующем пределе полином числителя имеет вторую степень, а полином знаменателя — третью степень, поэтому решение предела равно 0.</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
![]()
Посмотрите на другой пример, в котором два многочлена рациональной функции имеют вторую степень, поэтому мы должны разделить коэффициенты членов более высокой степени, чтобы вычислить предел на бесконечности.
![]()
Наконец, в следующем пределе функция числителя имеет большую степень, чем функция знаменателя, поэтому неопределенность бесконечности на бесконечности дает бесконечность. Кроме того, из числителя получается положительная бесконечность, а из знаменателя – отрицательная бесконечность, поэтому результат предела отрицательный (положительное значение между отрицательными является отрицательным).
![]()
Бесконечная неопределенность между бесконечностью с корнями
С другой стороны, степень иррациональной функции (функции с корнями) представляет собой частное между степенью главного члена и индексом радикала.
![Rendered by QuickLaTeX.com \sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffc00917d2cc316211a57feafdddd0d2_l3.png)
Следовательно, если предел функции с корнями дает бесконечную неопределенность между бесконечностью , мы должны применить те же правила, объясненные выше, относительно степеней числителя и знаменателя, но с учетом того, что степень многочлена с корнями вычисляется по-другому.
Посмотрите на следующий пример бесконечного предела функции с радикалами:
![]()
Степень числителя равна 2, а степень знаменателя равна 4 (8/2=4), поэтому предел равен 0, поскольку степень числителя меньше степени знаменателя.
Бесконечная неопределенность между бесконечностью и показательными функциями
Рост показательной функции намного больше, чем рост полиномиальной функции, поэтому мы должны учитывать, что степень показательной функции больше, чем степень полиномиальной функции.
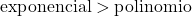
![]()
В этом примере знаменатель формируется из показательной функции, поэтому он имеет более высокий порядок, чем числитель. Следовательно, неопределенная форма бесконечность между бесконечностью дает 0.
Бесконечность минус бесконечная неопределенность
Решение задачи «бесконечная минус бесконечная неопределенность» зависит от того, имеет ли функция дроби или корни. Итак, давайте посмотрим, как разрешить этот тип неопределенности для этих двух разных случаев.
Неопределенность бесконечная минус бесконечность с дробями
Когда при сложении или вычитании алгебраических дробей возникает неопределенность «бесконечность минус бесконечность» , мы должны сначала выполнить сложение или вычитание дробей, а затем вычислить предел.
Давайте посмотрим, как вычислить неопределенность бесконечность минус бесконечность в функции с дробями, пошагово решив пример:
![]()
Сначала попытаемся вычислить предел:
![]()
Но мы получаем неопределенность ∞-∞.
Сначала нам нужно вычесть дроби. Для этого приведем дроби к общему знаменателю, то есть умножим числитель и знаменатель одной дроби на знаменатель другой:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68e489c5833478cb20929ea07ae2971d_l3.png)
И теперь, когда обе дроби имеют одинаковый знаменатель, мы можем объединить их в одну дробь:
![]()
Оперируем числителем и знаменателем:
![]()
И, наконец, мы снова вычисляем предел:
![]()
В этом случае бесконечная неопределенность между бесконечностью дает +∞, поскольку степень числителя больше степени знаменателя.
Неопределенность бесконечная минус бесконечность с корнями
Когда при радикальном сложении или вычитании возникает бесконечная минус бесконечная неопределенность , мы должны сначала умножить и разделить функцию на сопряженное радикальное выражение, а затем найти предел.
Давайте посмотрим, как решить неопределенность бесконечность минус бесконечность в иррациональной функции, следуя пошаговому примеру:
![]()
Сначала попробуем решить предел функции с радикалами:
![]()
Однако мы получаем неопределенную форму ∞-∞. Итак, чтобы узнать, сколько неопределенности составляет бесконечность минус бесконечность, вам нужно применить описанную процедуру.
Поскольку функция имеет радикалы, умножим и разделим всю функцию на сопряженное иррациональное выражение:
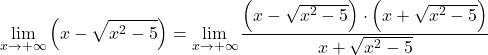
Алгебраическое выражение числителя соответствует заметному тождеству произведения суммы и разности, поэтому мы можем упростить выражение:
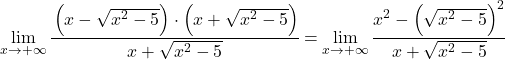
Теперь упростим корень предела, так как он возведен в квадрат:
![]()
Оперируем числителем дроби:
![]()
![]()
И, наконец, повторяем расчет лимита:
![]()
Таким образом, результат предела равен 0, поскольку любое число, разделенное на бесконечность, равно нулю.
Решенные упражнения на пределы на бесконечности
Упражнение 1
Найдите следующие пределы графика функции:
![]()
![]()
![]()
![]()
![]()
![]()
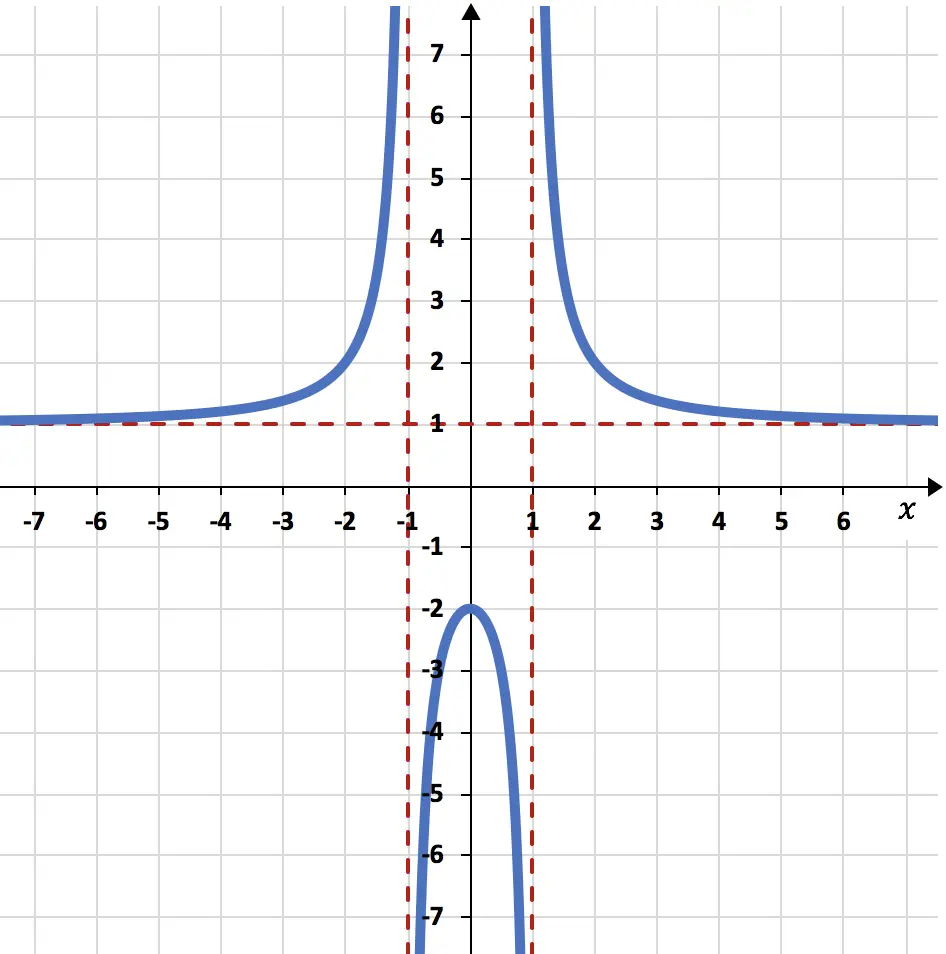
Предел функции, когда x стремится к минус бесконечности и плюс бесконечности, дает 1:
![]()
![]()
Боковые пределы функции слева и справа в точке x=-1 равны соответственно плюс бесконечность и минус бесконечность:
![]()
![]()
Наконец, боковые пределы функции, когда x стремится к 1, равны минус бесконечности и плюс бесконечности:
![]()
![]()
Упражнение 2
Решите предел при приближении x к бесконечности следующей функции:
![]()
Чтобы найти предел на бесконечности, нам нужно заменить x на бесконечность в члене полинома высшей степени:
![]()
Упражнение 3
Вычислите предел бесконечности следующей полиномиальной функции:
![]()
Чтобы найти предел на бесконечности, мы заменяем x на бесконечность в старшем члене полинома и выполняем вычисления:
![]()
Упражнение 4
Решите хотя бы бесконечный предел следующей полиномиальной функции:
![]()
Чтобы вычислить предел на бесконечности, мы заменяем x на минус бесконечность в старшем члене полинома и вычисляем функцию:
![]()
Поскольку минус бесконечность возведена в квадрат, знак бесконечности становится положительным.
Упражнение 5
Найдите предел на бесконечности следующей рациональной функции:
![]()
Чтобы определить предел бесконечности, заменим x на плюс бесконечность в члене высшей степени числителя и знаменателя дроби:
![]()
Помните, что любое число, разделенное на плюс или минус бесконечность, равно 0.
Упражнение 6
Решите следующий предел на бесконечности:
![]()
Чтобы вычислить предел, когда x стремится к ±∞ функции, просто посмотрите на моном высшей степени функции:
![]()
Упражнение 7
Вычислите предел следующей функции, когда x приближается к отрицательной бесконечности:
![]()
В этом случае достаточно заменить квадратичный член бесконечностью:
![]()
Упражнение 8
Найдите предел следующей показательной функции при приближении x к бесконечности:
![]()
Хотя это экспоненциальная функция, процесс решения предела тот же: замените x на бесконечность.
![]()
Упражнение 9
Решите бесконечный предел следующей показательной функции:
![]()
Чтобы устранить этот предел, необходимо использовать свойства дробей:
![]()
Упражнение 10
Решите следующий предел на бесконечности:
![]()
Предел дает неопределенность минус бесконечность между плюс бесконечность. Степень числителя больше степени знаменателя, поэтому неопределенный предел равен плюс бесконечности. Однако, поскольку при делении есть отрицательная бесконечность на положительную бесконечность, результатом является отрицательная бесконечность.
![]()
Упражнение 11
Исправьте следующий неопределенный предел:
![]()
В этой задаче неопределенная форма бесконечность по бесконечности получается из частного двух многочленов одной и той же степени, поэтому результатом неопределенного предела является деление их главных коэффициентов:
![]()
Упражнение 12
Вычислите следующий предел хотя бы до бесконечности:
![]()
Степень алгебраического выражения числителя меньше степени выражения знаменателя, поэтому неопределенность +∞/+∞ дает 0:
![]()
Упражнение 13
Решите следующий неопределенный предел функции с корнями:
![]()
Выражение числителя находится под радикалом, поэтому его степень равна 7/3. С другой стороны, полином знаменателя является квадратичным. А поскольку 7/3>2, предел дает еще большую бесконечность:
![]()
Упражнение 14
Определите бесконечный предел следующей функции с дробями:
![]()
В этом упражнении мы получаем неопределенность минус бесконечность, разделенную на минус бесконечность со степенью числителя больше степени знаменателя, следовательно:
![]()
Упражнение 15
Найдите хотя бы бесконечный предел следующей функции:
![]()
Полином знаменателя является квадратичным, а полином числителя линейным. Следовательно, бесконечная неопределенность, разделенная на бесконечность, дает 0.
![]()
Упражнение 16
Решите хотя бы бесконечный предел следующей функции:
![]()
Числитель на одну степень больше знаменателя, поэтому результат неопределенной формы ∞/∞ будет бесконечным. Кроме того, знак бесконечности будет отрицательным, поскольку положительное между отрицательными переводится в отрицательное:
![]()
Упражнение 17
Решите следующий предел на бесконечности:
![]()
Показательная функция имеет более высокий порядок, чем полиномиальная функция, поэтому предел будет давать бесконечность. Однако, разделив положительное на отрицательное, знак бесконечности будет отрицательным:
![]()
Упражнение 18
Вычислите бесконечный предел следующей функции с квадратным корнем:
![]()
Числитель состоит из квадратного корня, поэтому его степень равна 2/2=1. Тогда степень числителя равна степени знаменателя, поэтому бесконечная неопределенность между бесконечностью разрешается следующим образом:
![]()
Упражнение 19
Решите бесконечный предел следующей функции с двумя радикалами:
![]()
Степень числителя 7/3=2,33, степень знаменателя 5/2=2,5. Следовательно, поскольку степень числителя меньше степени знаменателя, неопределенный бесконечный предел между бесконечностью равен 0:
![Rendered by QuickLaTeX.com \displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-681401701d7d7f3fad1879db26659942_l3.png)
Упражнение 20
Рассчитайте следующий предел:
![]()
Независимо от степени числителя, поскольку в знаменателе у нас показательная функция, результат неопределенной формы, бесконечной над бесконечностью, равен 0:
![]()
Упражнение 21
Определите бесконечный предел следующей рациональной функции:
![]()
Сначала попытаемся вычислить предел, подставив в функцию бесконечность:
![]()
Но мы находим неопределенность ∞ – ∞. Поэтому приведем дроби к общему знаменателю:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e2820674bc86d085f6deec7fdf9adf8_l3.png)
И поскольку теперь обе дроби имеют одинаковый знаменатель, мы можем объединить их в одну дробь:
![]()
Заключаем скобки числителя:
![]()
И наконец, определяем предел:
![]()
В этом случае неопределенность ∞/∞ дает +∞, поскольку степень числителя больше степени знаменателя.
Упражнение 22
Решите предел следующей дробной функции, когда x приближается к 0:
![]()
Сначала попробуем вычислить лимит как обычно:
![]()
Но мы получаем неопределенную форму ∞-∞. Поэтому нам необходимо привести дроби функции к общему знаменателю.
В данном случае x 4 кратно x 2 , поэтому просто умножив числитель и знаменатель второй дроби на x 2 мы добьемся того, что обе дроби будут иметь одинаковый знаменатель:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-876115dc1fb49e81373d70be5fdcfb5e_l3.png)
Теперь мы можем вычесть две дроби:
![]()
Пробуем разрешить лимит еще раз:
![]()
Но в итоге мы получаем неопределенность константы, начиная с нуля. Поэтому необходимо вычислить боковые пределы функции.
![]()
![]()
В заключение, поскольку два боковых предела функции в точке x=0 дают -∞, решение предела есть -∞:
![]()
Упражнение 23
Решите бесконечный предел следующей функции с корнями:
![]()
Пытаясь решить предел, получаем неопределенность бесконечность минус бесконечность:
![]()
Следовательно, поскольку в функции имеются радикалы, ее необходимо умножить и разделить на сопряженное радикальное выражение:
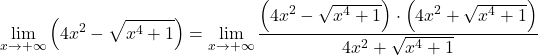
В числителе мы имеем примечательное произведение суммы и разности, равное разнице квадратов. Еще:
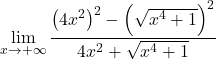
Упрощаем радикал до квадрата:
![]()
Оперируем числителем:
![]()
![]()
И наконец находим предел:
![]()
В этом случае неопределенность бесконечность, разделенная на бесконечность, является более бесконечной, поскольку степень числителя больше степени знаменателя (напомним, что квадратный корень уменьшает степень на два:
![]()
).
Упражнение 24
Решите предел при стремлении x к бесконечности следующей иррациональной функции:
![]()
Сначала попробуем вычислить лимит как обычно:
![]()
Но это приводит к неопределенности разности бесконечностей. Следовательно, поскольку функция имеет корни, необходимо умножить и разделить выражение на сопряженный радикал:
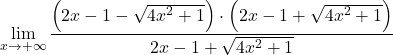
Сгруппируем примечательное равенство числителя дроби:
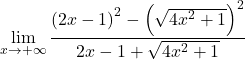
Решаем квадратный корень:
![]()
Решаем примечательное тождество квадрата разности:
![]()
Оперируем числителем:
![]()
![]()
И наконец, вычисляем значение предела на бесконечности:
![]()
Несмотря на то, что в знаменателе стоит квадрат х, на самом деле его степень равна 1, поскольку он находится внутри корня:
![]()
Следовательно, результатом неопределенности -∞/+∞ является деление коэффициентов при x высшей степени, так как степень числителя равна степени знаменателя.
![]()
Заметим, что поскольку в знаменателе имеются два члена первой степени
![]()
И
![]()
, чтобы разрешить неопределенность -∞/+∞, необходимо взять все коэффициенты членов первой степени, то есть
![]()
из
![]()
и
![]()
из
![]()
Упражнение 25
Рассчитайте предел при приближении x к 1 следующей функции с дробями:
![]()
Пытаясь установить предел, мы получаем неопределенный предел бесконечности минус бесконечность:
![]()
Поэтому мы должны привести дроби к общему знаменателю, или, другими словами, мы должны умножить числитель и знаменатель одной дроби на знаменатель другой:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-75bf3ffa177f32711c5509ce5fe5992d_l3.png)
И поскольку теперь обе дроби имеют одинаковый знаменатель, мы можем сложить их вместе:
![]()
Мы работаем:
![]()
![]()
И мы снова пытаемся решить предел:
![]()
Но мы находим ноль неопределенности, разделенный на ноль. Поэтому мы должны факторизовать полиномы числителя и знаменателя:
![]()
Теперь упростим дробь, убрав множитель, который повторяется в числителе и знаменателе:
![]()
И, наконец, мы разрешаем предел:
![]()