Полиномиальная функция

Здесь вы узнаете, что такое полиномиальные функции и что представляют собой все виды полиномиальных функций. Кроме того, мы также объясняем свойства полиномиальных функций.

Что такое полиномиальная функция?

Полиномиальная функция — это функция, алгебраическим выражением которой является полином , то есть полиномиальная функция определяется сложением или вычитанием конечного числа членов разной степени.

Следовательно, полиномиальная функция математически описывается следующим выражением:

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

С другой стороны, полиномиальные функции также можно определить с помощью следующей формулы:

$\displaystyle f(x)=\sum_{k=0}^{n}a_k\cdot x^k$

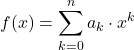
где условия

$a_k$

$x^k$

являются соответственно коэффициентом и переменной каждого монома, образующего полиномиальную функцию.

Термин

$a_nx^n$

, называемый основным членом, указывает степень полиномиальной функции, поскольку это моном самой высокой степени функции. Другими словами, показатель наибольшего значения — это тот, который указывает степень полиномиальной функции.

Хотя ниже мы увидим больше характеристик полиномиальных функций, областью определения любой полиномиальной функции являются все действительные числа.

Виды полиномиальных функций

Учитывая определение полиномиальной функции, мы теперь увидим, какие типы полиномиальных функций существуют.

постоянная функция

Функция-константа — это полиномиальная функция степени 0, поэтому это тип функции, которая всегда принимает один и тот же образ для любого значения независимой переменной (x).

Общее выражение для постоянной функции выглядит следующим образом:

$f(x)=k$

Например, следующие три функции являются константами или полиномиальными функциями нулевой степени:

$f(x)=5 \qquad f(x)=2 \qquad f(x)=-3$

Графическое представление постоянной функции представляет собой горизонтальную линию (параллельную оси X) со значением, равным константе.

Дополнительные возможности этого типа функций вы можете увидеть по следующей ссылке:

➤ См.: характеристики постоянной функции

Линейная функция

Линейная функция , также называемая аффинной функцией, является полиномиальной функцией первой степени. Таким образом, полиномиальная функция этого типа может состоять только из линейного члена и независимого члена:

$f(x)=mx+n$

Золото

$m$

это наклон линии и

$n$

— это точка пересечения оси Y, т. е. точка пересечения функции оси Y.

Примеры линейных функций или полиномиальных функций первой степени:

$f(x)=4x+3\qquad f(x)=-5x$

Некоторые отличают линейную функцию от аффинной функции в зависимости от того, имеет ли функция своим членом

$n$

или нет, будучи аффинной функцией с точкой пересечения и линейной функцией без нее.

Графическим изображением линейных функций всегда являются линии, степень наклона которых зависит от значения наклона функции.

Ниже вы можете графически увидеть полиномиальную функцию первой степени.

$f(x)=2x-1.$

Однако, чтобы построить график линейной функции, вам необходимо четко понимать несколько понятий. По следующей ссылке вы найдете пошаговое объяснение того, как построить график полиномиальной функции этого типа:

➤ См.: Графическое представление линейной функции.

Квадратичная функция

Квадратичная функция — это полиномиальная функция степени 2, то есть функция, член старшей степени которой имеет вторую степень.

Следовательно, формула квадратичной функции имеет вид:

$f(x)=ax^2+bx+c$

Золото

$ax^2$

квадратичный член,

$bx$

линейный член и

$c$

независимый член полиномиальной функции.

Примеры квадратичных функций или квадратичных полиномиальных функций:

$f(x)=5x^2+2x-1\qquad f(x)=-2x^2+x+7$

График квадратичной функции всегда представляет собой параболу и его форма зависит от знака старшего коэффициента.

$a:$

Если коэффициент
$a$

положительна, квадратичная функция выпукла (имеет вид

$\bm{\cup}$

).
Вместо этого, если коэффициент
$a$

отрицательна, квадратичная функция вогнута (имеет форму

$\bm{\cap}$

).

Итак, зная знак главного коэффициента квадратичной полиномиальной функции, мы можем знать форму, которую примет ее график, но для того, чтобы сделать ее точное графическое представление, необходимо выполнить определенную процедуру. Эту процедуру вы можете увидеть по следующей ссылке:

➤ См.: Графическое представление квадратичной функции.

кубическая функция

Кубическая функция – это полиномиальная функция третьей степени. Следовательно, этот тип полиномиальных функций выражается алгебраически следующим образом:

$f(x)=ax^3+bx^2+cx+d$

Примеры кубических функций или полиномиальных функций третьей степени:

$f(x)=x^3+4x^2+5x-1$

$f(x)=2x^3-3x^2+9$

Графические представления кубических функций соответствуют кубическим кривым. Однако для представления функций этого типа на графике необходимо выполнить сложную процедуру (она включает в себя производные). Посмотреть, как это делается, можно здесь:

➤ См.: Как представить функцию

Как видите, типы полиномиальных функций на самом деле бесконечны, поскольку полином может иметь бесконечные члены. Так, например, функция четвертой степени похожа на кубическую функцию, но с добавлением квадратичного члена. Важно то, что вы понимаете, что тип полиномиальной функции определяется степенью функции.

Свойства полиномиальных функций

Полиномиальные функции имеют следующие характеристики:

Областью определения любой полиномиальной функции является множество действительных чисел.

$\text{Dom } f=\mathbbf{R}$

Все полиномиальные функции непрерывны.

Полиномиальные функции степени больше 1 не имеют асимптот.

Независимо от типа полиномиальной функции, единственная точка пересечения с осью ординат (ось Y) находится на высоте ее независимого члена, то есть в следующей точке:

$(0,a_0)$

С другой стороны, полиномиальная функция пересекает ось абсцисс (ось X) не более того столько раз, сколько степень функции.

Если полиномиальная функция имеет члены только четной степени, это означает, что она симметрична относительно оси OY. С другой стороны, если полиномиальная функция имеет члены только нечетной степени, это означает, что функция симметрична относительно начала координат.

Число относительных экстремумов (максимума или минимума) полиномиальной функции не превышает степени многочлена функции минус 1.

Число точек перегиба полиномиальной функции не более равно степени многочлена функции минус 2.

Операции можно выполнять с полиномиальными функциями:
- Сумма двух полиномиальных функций дает еще одну полиномиальную функцию.
- Произведение двух полиномиальных функций порождает другую полиномиальную функцию.
- Умножение полиномиальной функции на скаляр (действительное число) приводит к аналогичной полиномиальной функции, но с уменьшенным или расширенным графиком.
- Композиция двух полиномиальных функций равна другой полиномиальной функции.