На этой странице вы найдете, что такое перпендикулярные плоскости, как определить, перпендикулярны ли две плоскости, как рассчитать перпендикулярную плоскость, примеры и решенные упражнения с перпендикулярными плоскостями,…
Что такое две перпендикулярные плоскости?
В аналитической геометрии две плоскости перпендикулярны, если они пересекаются под прямым углом (90°).
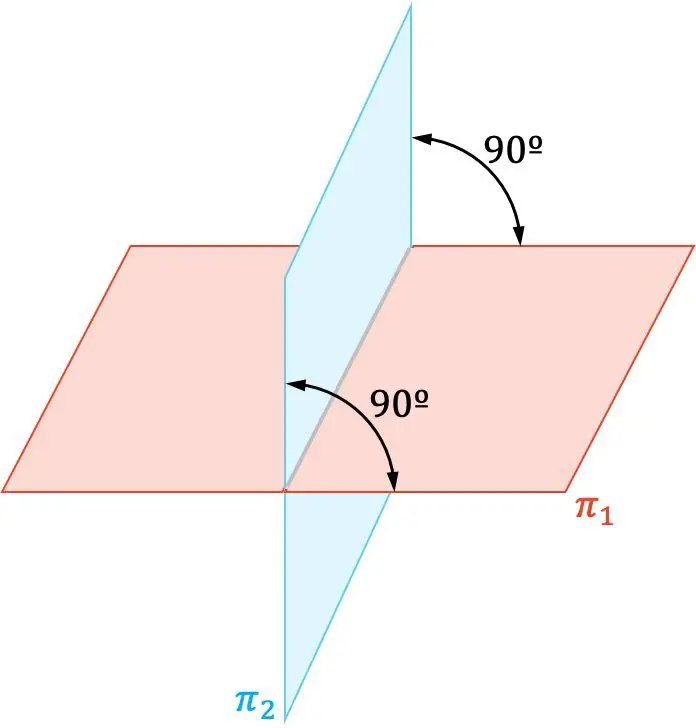
При этом векторы нормалей двух перпендикулярных плоскостей также ортогональны друг другу.
Очевидно, что расстояние между двумя перпендикулярными плоскостями всегда равно нулю, поскольку они пересекаются по прямой. Хотя это кажется очень простым, понятие расстояния между двумя плоскостями очень важно, поэтому мы рекомендуем перейти по ссылке, если у вас есть какие-либо вопросы по этому поводу.
С другой стороны, две плоскости, расположенные перпендикулярно, не являются единственно возможным относительным положением между плоскостями, поскольку две плоскости в пространстве (в R3) также могут быть пересекающимися, параллельными или совпадающими.
Как узнать, перпендикулярна ли одна плоскость другой?
После того, как мы увидели определение перпендикулярных плоскостей, давайте посмотрим, как узнать, перпендикулярны две плоскости или нет:
Две плоскости перпендикулярны, если их нормали перпендикулярны. Следовательно, чтобы определить, перпендикулярны ли две плоскости друг другу, мы должны вычислить угол, образованный их векторами нормалей, и если они образуют угол 90°, это означает, что плоскости перпендикулярны.
Итак, чтобы найти перпендикулярность двух плоскостей, вам нужно знать , как вычислять угол между двумя векторами . Если вы не помните, как это сделать, вы можете обратиться по ссылке, где вы найдете наше объяснение, а также необходимую формулу для определения угла между двумя векторами. Кроме того, вы сможете увидеть примеры и попрактиковаться на решенных упражнениях.
Короче говоря, два вектора перпендикулярны, если их скалярное произведение равно нулю. Следовательно, две плоскости будут перпендикулярны, если скалярное произведение соответствующих векторов нормалей равно 0.
Пример двух перпендикулярных плоскостей
Например, давайте проверим, перпендикулярны ли следующие две плоскости:
![]()
![]()
Координаты X, Y, Z вектора нормали к плоскости совпадают с коэффициентами A, B, C ее общего (или неявного) уравнения. Следовательно, вектор нормали к каждой плоскости равен:
![]()
![]()
А теперь проверим, являются ли это две перпендикулярные плоскости, вычисляя скалярное произведение между их векторами нормалей:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94cfcef6a93720224eff0bd4891839ed_l3.png)
Скалярное произведение двух векторов нормалей равно 0, поэтому две плоскости перпендикулярны друг другу.
Вычислить плоскость, перпендикулярную прямой в точке
Типичная задача о плоскостях и прямых — найти уравнение плоскости, перпендикулярной прямой в данной точке. Итак, далее мы увидим, как она решается на примере:
- Найдите уравнение плоскости, перпендикулярной прямой.

О
сказано прямо и в точку:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ac7260ee9792daec4f32e1f200df01b_l3.png)
Сначала нам нужно найти вектор, нормальный к рассматриваемой плоскости. и мне нравится прямая линия
![]()
перпендикулярна плоскости, то ее вектор нормали будет совпадать с вектором направления прямой.
В этом случае линия
![]()
находится в форме параметрических уравнений, поэтому компонентами его вектора направления являются члены перед параметром
![]()
![]()
Таким образом, вектор нормали к плоскости будет таким же, как вектор направления прямой:
![]()
И, следовательно, неявное (или общее) уравнение плана будет следующим:
![]()
Поэтому достаточно определить значение коэффициента D. Для этого подставим в его уравнение координаты точки, утверждение которой говорит нам о принадлежности ее плоскости:
![]()
![]()
![]()
![]()
![]()
Короче говоря, декартово уравнение плоскости:
![]()
С другой стороны, если вы хотите попрактиковаться в дополнительных упражнениях на перпендикулярность между геометрическими объектами, вы можете посетить нашу страницу о перпендикулярных линиях. Вы найдете все, что вам нужно знать о перпендикулярных линиях : когда две прямые перпендикулярны, как вычислить один перпендикуляр к другому, примеры, решенные упражнения и многое другое.
Свойства перпендикулярных плоскостей
Все перпендикулярные плоскости имеют следующие характеристики:
- Симметричные отношения : если плоскость перпендикулярна другой плоскости, эта плоскость также перпендикулярна первой плоскости. Этим свойством обладают и параллельные плоскости.
![]()
- Нерефлексивное свойство : очевидно, что ни одна плоскость не может быть перпендикулярна самой себе.
![]()
- Теорема: В трехмерном (3D) пространстве любая пара плоскостей, перпендикулярных третьей плоскости, обязательно должна быть параллельной. Другими словами, если плоскость перпендикулярна другой плоскости, а эта плоскость также перпендикулярна третьей плоскости, то первая и последняя плоскости параллельны друг другу.