Перпендикулярные линии (перпендикулярность) -

На этой странице вы найдете все о перпендикулярных линиях: что это такое, когда две линии перпендикулярны, как вычислить линию, перпендикулярную другой, ее свойства… Кроме того, вы сможете увидеть примеры и сможете практика с упражнениями, решенными шаг за шагом.

Что такое две перпендикулярные прямые?

В математике две прямые считаются перпендикулярными, если они пересекаются в точке, образующей четыре равных прямых угла (90°).

Кроме того, векторы направления двух перпендикулярных прямых также должны быть перпендикулярны.

Перпендикулярность двух линий обычно обозначается символом

$\perp .$

С другой стороны, помните, что на плоскости существует 4 возможности понятия относительного положения между двумя прямыми: две прямые могут быть секущими, перпендикулярными, совпадающими или параллельными. При желании вы можете проверить значение каждого типа линий на нашем сайте.

Как узнать, перпендикулярны ли две прямые?

Есть два способа определить, когда две линии перпендикулярны: по их направляющим векторам или по их наклонам . Ниже вы найдете объяснение обоих методов, хотя они служат одной и той же цели, мы рекомендуем вам знать, как выполнять обе процедуры, поскольку каждая из них зависит от того, как выражены линии.

По векторам направления линий

Один из способов узнать, перпендикулярны ли две прямые, — это использовать векторы направления рассматриваемых линий. Помните, что вектор направления — это вектор, указывающий направление линии.

Векторы направления двух перпендикулярных прямых также взаимно ортогональны. Следовательно, если скалярное произведение векторов направления двух прямых равно 0, это означает, что линии перпендикулярны.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

Давайте посмотрим, как определяется перпендикулярность двух линий на примере:

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

Обе линии выражаются в виде параметрических уравнений, поэтому компонентами вектора направления каждой линии являются числа перед параметром

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

Как только мы узнаем вектор направления каждой линии, мы проверяем, перпендикулярны ли они, вычисляя произведение векторов:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

Скалярное произведение двух векторов равно нулю, поэтому линии перпендикулярны.

Уклоны линий

Другой способ определить, перпендикулярны ли две линии, — использовать их наклоны. Помните, что наклон линии – это коэффициент

$m$

явного уравнения и уравнения точки-наклона прямой.

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

А наклон линии также можно получить из коэффициентов

$A$

$B$

неявного (или общего) уравнения прямой:

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

Таким образом, наклоны двух перпендикулярных прямых обратны и имеют противоположный знак, то есть всегда выполняется следующее равенство:

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

Итак , если произведение наклонов двух разных линий равно -1, это означает, что линии перпендикулярны:

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

Например, следующие две прямые перпендикулярны:

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

Мы можем показать, что это две прямые, перпендикулярные друг другу по своим наклонам. Наклон каждой линии равен:

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

Теперь умножаем наклоны:

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

Произведение двух наклонов эквивалентно -1, что фактически означает две линии, перпендикулярные друг другу.

Как рассчитать линию, перпендикулярную другой?

Хоть это и может показаться трудным, но найти линию, перпендикулярную другой, довольно просто, для этого нужен только вектор направления, перпендикулярный прямой, и точка, принадлежащая этой линии.

Единственная трудность состоит в том, что, как и раньше, процедура зависит от типа уравнения, в котором выражены линии. Потому что линию, перпендикулярную другой, можно вычислить по векторам направления или по наклонам .

От вектора направления вправо

Линию, перпендикулярную другой данной прямой, можно найти, используя ее вектор направления. Давайте посмотрим, как это делается на примере:

Вычислить линию, перпендикулярную прямой
$r$

что проходит через точку

$P(5,-1)$

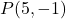
. быть прямым

$r:$

$\displaystyle r : \ 3x+2y-1=0$

Первое, что нам нужно сделать, это определить вектор направления линии. В этом случае линия определяется в виде общего (или неявного) уравнения, поэтому декартовы координаты вектора направления линии можно получить с помощью коэффициентов А и В линии:

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

И как только мы знаем вектор направления линии, мы должны вычислить вектор, перпендикулярный ему. Для этого просто вставьте координаты вектора и измените знак одного из них (того, который вам нужен):

$\vv{\text{v}}_\perp =(3,2)$

Итак, теперь мы знаем вектор направления линии. Таким образом, неявное уравнение линии будет иметь следующий вид:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

Поэтому достаточно определить параметр С. Для этого подставим в ее уравнение точку, принадлежащую прямой, и решим полученное уравнение:

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

В заключение уравнение перпендикулярной линии имеет вид:

$\bm{2x-3y-13=0}$

От наклона линии

Другой способ найти линию, перпендикулярную определенной линии, — по ее наклону. Давайте посмотрим, как решается задача такого типа на примере:

Вычислить линию, перпендикулярную прямой
$r$

что проходит через точку

$P(0,1)$

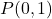
. быть прямым

$r:$

$\displaystyle r : \ y=4x-3$

Наклон линии

$r$

Восток:

$m_r = 4$

Зная наклон прямой, нам нужно найти наклон перпендикулярной линии. Как мы видели в разделах выше, наклоны двух перпендикулярных линий обратны и имеют измененный знак. Следовательно, чтобы определить наклон перпендикулярной линии, нам необходимо инвертировать найденный наклон и изменить его знак:

$m_\perp =-\cfrac{1}{4}$

Таким образом, явное уравнение перпендикулярной линии будет следующим:

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

Наконец, вычислим ординату начала перпендикулярной линии, подставив координаты точки в уравнение прямой:

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

Короче говоря, уравнение перпендикулярной линии:

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

Свойства перпендикулярных линий

Все перпендикулярные линии имеют следующие характеристики:

Симметричные отношения : если линия перпендикулярна другой линии, эта линия также перпендикулярна первой линии.

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

Нерефлексивное свойство : очевидно, что ни одна линия не может быть перпендикулярна самой себе.

$r \ \cancel{\bm{\perp}}} \ r$

Теорема: В евклидовой геометрии (в R2) любая пара прямых, перпендикулярных третьей прямой, обязательно должна быть параллельной. То есть, если линия перпендикулярна другой линии, а эта линия также перпендикулярна третьей линии, первая и последняя линии параллельны.

Решенные задачи о перпендикулярных прямых

Упражнение 1

Какая из следующих прямых перпендикулярна прямой

$r: y=3x+4$

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

посмотреть решение

Наклон линии

$r$

это 3:

$m_r=3$

А наклоны двух перпендикулярных прямых обратны и имеют противоположный знак, поэтому наклон любой прямой, перпендикулярной прямой,

$r$

должно быть:

$m_\perp=-\cfrac{1}{3}$

Чтобы линии были перпендикулярны прямой

$r$

это те, наклон которых равен

$-\cfrac{1}{3}$

. То есть строки

$\bm{b}$

$\bm{e}.$

Упражнение 2

Определите, перпендикулярны ли следующие две прямые:

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

посмотреть решение

право

$r$

выражается в виде параметрического уравнения, такого, что компонентами вектора направления указанной прямой являются числа перед параметром

$t:$

$\vv{\text{v}}_r =(-1,-3)$

С другой стороны, прямая линия

$s$

определяется в виде непрерывного уравнения, поэтому координатами его вектора направления являются числа знаменателей:

$\vv{\text{v}}_s =(4,6)$

Зная вектор направления каждой линии, мы можем проверить, перпендикулярны ли они, вычислив произведение двух векторов:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

Скалярное произведение двух векторов не равно нулю, поэтому линии не перпендикулярны .

Упражнение 3

Найдите линию, перпендикулярную прямой

$r$

что проходит через точку

$P(-2,1)$

. быть прямым

$r:$

$\displaystyle r : \ 4x-y+5=0$

посмотреть решение

Первое, что нам нужно сделать, это определить вектор направления линии. В этом случае линия определяется в виде общего (или неявного) уравнения, поэтому ее вектор направления равен:

$\vv{\text{v}}_r =(-B,A)=(1,4)$

Зная вектор направления линии, нам нужно вычислить вектор, перпендикулярный ему. Для этого просто вставьте координаты вектора и измените знак одного из них (того, который вам нужен):

$\vv{\text{v}}_\perp =(4,-1)$

Таким образом, неявное уравнение линии будет иметь следующий вид:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$

$Ax+By+C \ \longrightarrow \ -x-4y+C=0$

Поэтому достаточно определить неизвестное C. Для этого подставим в его уравнение точку, через которую проходит прямая:

$P(-2,1)$

$-x-4y+C=0 \ \xrightarrow{x=-2 \ ; \ y=1} \ -(-2)-4\cdot 1+C=0$

$2-4+C=0$

$-2+C=0$

$C=2$

Наконец, уравнение перпендикулярной линии:

$\bm{-x-4y+2=0}$

Упражнение 4

Найдите уравнение наклона точки линии, перпендикулярной прямой.

$r$

что проходит через точку

$P(3,-2)$

. быть прямым

$r:$

$\displaystyle r : \ y=5x+1$

посмотреть решение

Наклон линии

$r$

Восток:

$m_r = 5$

Зная наклон прямой, нам нужно найти наклон перпендикулярной линии. Для этого просто переверните найденный наклон и измените его знак:

$m_\perp =-\cfrac{1}{5}$

Наконец, просто подставьте найденный наклон и координаты точки в уравнение наклона точки линии:

$y -y_0=m(x-x_0)$

$y-(-2)=-\cfrac{1}{5} (x- 3)$

$\bm{y+2=}\mathbf{-\cfrac{1}{5}}\bm{ (x- 3)}$

Упражнение 5

право

$r$

проходит через точки (2,1) и (4,2), а линия

$s$

проходит через точки (-1,2) и (1,-2). Определите, являются ли это две перпендикулярные прямые или нет.

посмотреть решение

Чтобы проверить, являются ли это две перпендикулярные линии, мы рассчитаем их наклоны, а затем посмотрим, соблюдаются ли они перпендикулярные отношения. Помните, что формула наклона линии такова:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Наклон линии

$r$

Восток:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{2-1}{4-2} = \cfrac{1}{2}$

Наклон линии

$s$

Восток:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{-2-2}{1-(-1)} = \cfrac{-4}{2}=-2$

Чтобы проверить перпендикулярность двух линий, мы должны увидеть, является ли наклон одной линии обратным наклону другой. В этом случае два наклона являются обратными и имеют противоположные знаки, поэтому две линии перпендикулярны друг другу.

Упражнение 6

Рассчитайте стоимость

$k$

так, чтобы следующие две прямые были перпендикулярны:

$\displaystyle r: \ 5x+3y-7=0\qquad \qquad s: \ 4x+ky+1=0$

посмотреть решение

Две линии выражаются в форме неявного (или общего) уравнения, а вектор направления неявного уравнения линии равен:

$Ax+By+C=0$

$\vv{\text{v}} =(-B,A)$

Следовательно, вектор направления каждой линии будет:

$\vv{\text{v}}_r =(-3,5) \qquad \qquad \vv{\text{v}}_s =(-k,4)$

Чтобы две прямые были перпендикулярны, скалярное произведение их векторов направления должно быть равно нулю. Поэтому мы применим это условие, чтобы найти значение неизвестного

$k:$