Параллельные линии

Здесь вы найдете все о параллельных прямых: что они означают, как определить, параллельны ли две прямые, их свойства и т.д. Кроме того, вы сможете увидеть несколько примеров и решенных упражнений на параллельные линии.

Что такое параллельные прямые?

Параллельные линии — это линии, которые никогда не пересекаются, то есть, даже если их траектории простираются до бесконечности, они никогда не касаются друг друга. Следовательно, точки двух параллельных прямых всегда находятся на одинаковом расстоянии друг от друга и, более того, две параллельные прямые не имеют общих точек.

Например, следующие две линии параллельны:

Обычно мы указываем, что две линии параллельны двум вертикальным полосам || между линиями

С другой стороны, несмотря на то, что две параллельные прямые никогда не пересекаются, в аналитической геометрии мы говорим, что они образуют угол 0°, поскольку имеют одно и то же направление.

Когда две прямые параллельны?

Увидев определение параллельных прямых, мы увидим, как найти две параллельные прямые. Очевидно, что одним из способов было бы построить график линий и посмотреть, пересекаются ли они на графике, но есть еще более простые и легкие в использовании методы.

Определить параллельность двух прямых по их наклонам.

Вы можете определить, когда две линии параллельны, посмотрев на наклон каждой линии. Помните, что наклон линии — это параметр

$m$

из явного уравнения и уравнения наклона точки линии:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Однако существует несколько способов определения наклона линии, поэтому, чтобы узнать, как его рассчитать, рекомендуем взглянуть на формулу наклона линии . Кроме того, на связанной странице вы также найдете объяснение того, что представляет собой наклон линии и почему это так важно для линии.

Таким образом, на плоскости две прямые параллельны, если они имеют одинаковый наклон (коэффициент m) и разные ординаты в начале координат (коэффициент n) .

Например, следующие две линии параллельны:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

Это две параллельные прямые, потому что они обе имеют одинаковый наклон и, более того, их независимые члены различны.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

Следует отметить, что если бы две линии имели одинаковый наклон и в то же время один и тот же компьютер в начале координат, они были бы идентичными линиями , потому что они были бы совершенно идентичными.

Найдите параллельность двух прямых из неявного уравнения

Помните, что неявное (или общее) уравнение линии имеет вид:

$Ax+By+C=0$

Таким образом, если коэффициенты А и В двух прямых пропорциональны друг другу, но не коэффициенту С , это означает, что прямые параллельны.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

Вот две параллельные линии, выраженные в общей (или неявной) форме уравнения:

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

Они параллельны, потому что числа перед переменной

$x$

пропорциональны числам перед переменной

$y$

, но не с независимыми членами.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

Как и раньше, если бы все коэффициенты (A, B и C) двух неявных прямых были пропорциональны, это означало бы, что эти две линии совпадают или, другими словами, они равны.

Свойства параллельных линий

Характеристики параллельных линий следующие:

Свойство симметричности : если одна линия параллельна другой, то и эта линия параллельна первой. Этим свойством обладают и перпендикулярные прямые.

$r \parallel s \ \longrightarrow \ s \parallel r$

Транзитивное свойство : если линия параллельна другой линии, а эта вторая линия параллельна третьей линии, то первая линия также параллельна третьей линии.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

Скалярное произведение векторов направления (вектор, указывающий направление линии) двух параллельных линий равно произведению их модулей.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

Кроме того, векторы направления двух параллельных прямых всегда линейно зависят друг от друга, поскольку они пропорциональны .

Это условие необходимо для параллельности линий, но недостаточно, или, другими словами, две параллельные линии должны иметь пропорциональные векторы направления, но тот факт, что две линии имеют пропорциональные векторы направления, не означает напрямую, что они параллельны. Поскольку совпадающие линии тоже имеют пропорциональные векторы направления.

Линии, параллельные оси абсцисс (оси X), горизонтальны и всегда имеют вид
$y=k.$

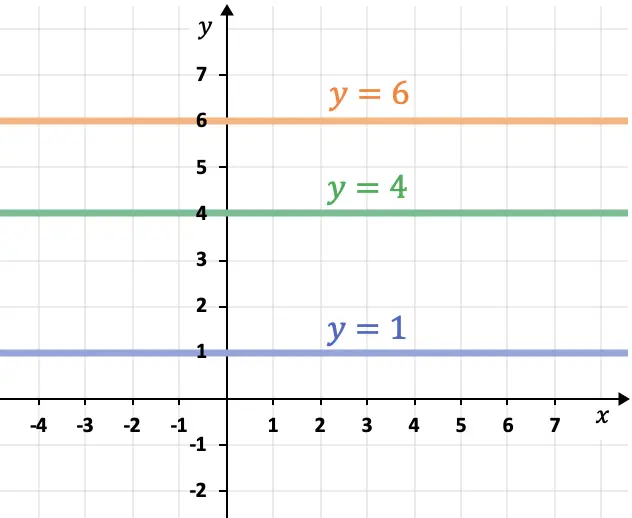
Линии, параллельные оси компьютера (ось Y), вертикальны и всегда соответствуют выражению
$x=k.$

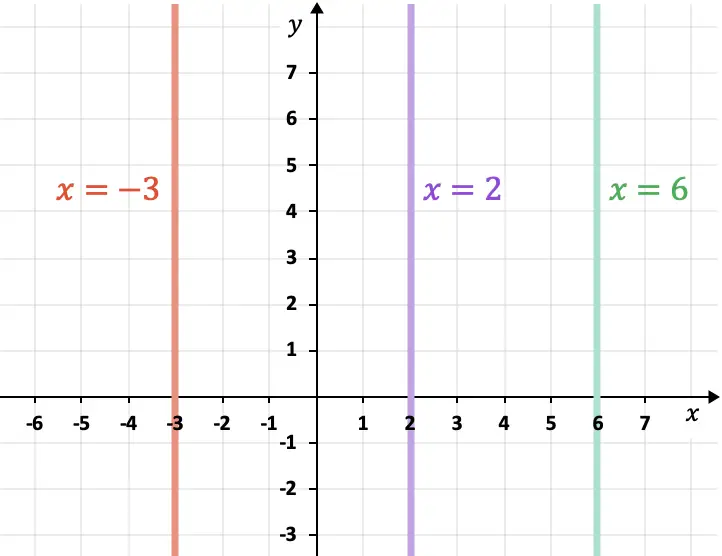
Как рассчитать расстояние между двумя параллельными прямыми на плоскости

Чтобы найти расстояние между двумя параллельными линиями на плоскости (в R2), просто возьмите точку на одной из двух линий и вычислите расстояние от этой точки до другой линии.

Мы можем сделать это таким образом, потому что две параллельные линии всегда находятся на одинаковом расстоянии друг от друга.

расстояние между двумя параллельными прямыми

С другой стороны, если при использовании формулы мы получим расстояние в 0 единиц, это означает, что линии в какой-то точке касаются друг друга и, следовательно, линии не параллельны, а пересекаются, совпадают или перпендикулярны. При желании вы можете проверить отличия этого типа линий на нашем сайте.

Итак, чтобы вы могли увидеть, как это делается, в качестве примера мы определим расстояние между следующими двумя параллельными линиями:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Первое, что нам нужно сделать, это поставить точку на одной из линий (той, которая вам нужна). В данном случае мы рассчитаем точку на линии

$s.$

Для этого мы должны присвоить значение одной из переменных, мы сделаем это, например

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

И теперь мы очищаем другую переменную (

$y$

) полученного уравнения, чтобы узнать, сколько оно стоит в данный момент:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Следовательно, точка, полученная из прямой

$s$

Восток:

$P(0,-2)$

И как только у нас уже есть точка на линии, мы вычисляем расстояние от этой точки до другой линии, используя формулу расстояния от точки до линии:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

Таким образом, расстояние между двумя параллельными линиями эквивалентно 0,45 единицы .

Решенные задачи параллельными линиями

Упражнение 1

Какие из следующих прямых параллельны?

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

посмотреть решение

Две прямые параллельны, если они имеют одинаковый наклон (и разные точки пересечения). Таким образом, наклон каждой линии равен:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

Значит только прямые параллельны

$r$

$q,$

потому что они единственные, кто имеет равные уклоны.

Упражнение 2

Найдите явное уравнение прямой, параллельной прямой

$r$

и что происходит через точку

$P(0,2).$

быть прямым

$r:$

$r: \; y=3x-1$

посмотреть решение

Чтобы линия была параллельна линии

$r,$

оба должны иметь одинаковый наклон. и наклон линии

$r$

это 3:

$m = 3$

Следовательно, явное уравнение линии, которую нам нужно найти, будет иметь вид:

$y=3x+n$

И как только мы узнаем наклон линии, мы можем вычислить точку пересечения, подставив точку, принадлежащую линии, в уравнение линии:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

Итак, явное уравнение линии:

$\bm{y=3x+2}$

Упражнение 3

Вычислить значение неизвестных

$a$

$b$

так, чтобы следующие две прямые были параллельны:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

посмотреть решение

Линии описываются в общей (или неявной) форме уравнений. Следовательно, чтобы две прямые были параллельны, их коэффициенты A и B должны быть пропорциональны, то есть должно выполняться следующее уравнение:

$\cfrac{2}{1} = \cfrac{-4}{a}$