Здесь вы найдете все о гиперболе: что это такое, каковы ее характерные элементы, как найти ее уравнение, примеры, решенные упражнения и т. д.
Что такое гипербола?
Гипербола представляет собой разомкнутую кривую с двумя ветвями, математическое определение которой следующее:
В аналитической геометрии гипербола — это геометрическое место точек на плоскости, удовлетворяющее следующему условию: абсолютное значение разности расстояний между любой точкой гиперболы и двумя неподвижными точками (называемыми фокусами) должно быть постоянным.
Более того, значение вычитания этих двух расстояний всегда эквивалентно расстоянию между двумя вершинами гиперболы.
![]()

Ниже мы увидим, что означает коэффициент
![]()
из гиперболы.
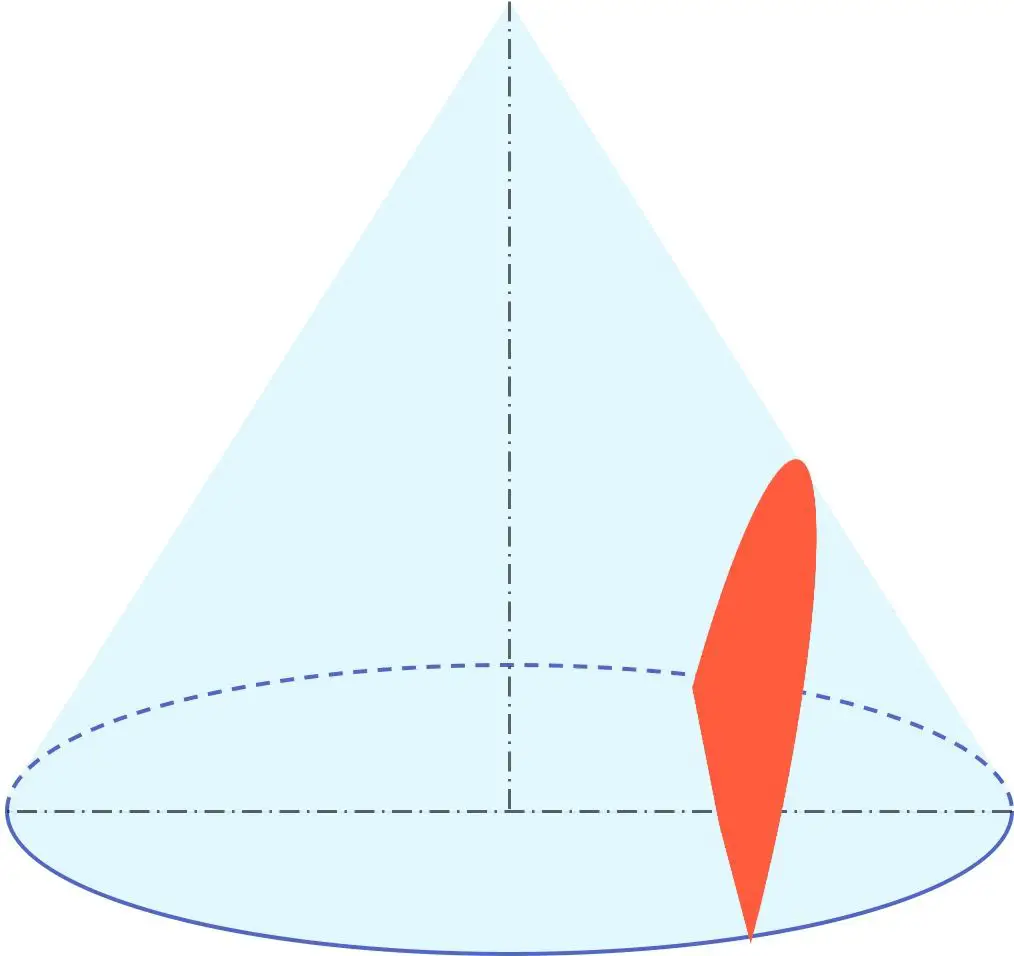
Кроме того, гипербола входит в геометрическую группу, называемую кониками, наряду с окружностью, эллипсом и параболой. Следовательно, гипербола представляет собой коническое сечение, или, другими словами, ее можно получить из конуса.
В частности, гипербола — это результат сечения конуса плоскостью с углом, меньшим угла, образуемого образующей конуса относительно его оси вращения.
Элементы гиперболы
Характеристики гиперболы зависят от следующих факторов:
- Фокусы : это две неподвижные точки, характерные для каждой гиперболы (точки F и F’ на графике ниже). Абсолютная величина разности расстояний от любой точки гиперболы до каждого фокуса постоянна и равна

- Фокальная или главная ось : это линия, проходящая через два фокуса гиперболы. Он соответствует оси симметрии указанной геометрической фигуры. Также называется поперечной или поперечной осью.
- Вторичная ось : это биссектриса отрезка FF’ (линия, проходящая через точки B и B’). Кроме того, это линия, перпендикулярная фокальной оси, и это еще одна ось симметрии гиперболы.
- Центр (O) : точка пересечения двух осей и середина двух вершин и двух фокусов. Поскольку гипербола имеет две оси симметрии, она также является центром симметрии.
- Вершины (А и А’) : точки пересечения ветвей гиперболы с фокальной осью.
- Векторные лучи (R) : это отрезки, идущие от любой точки гиперболы к каждому фокусу.
- Фокусное расстояние : это длина составного сегмента между двумя фокусами.
- Большая ось или действительная ось: это отрезок, идущий от точки А к точке А’, его длина эквивалентна

- Малая ось или мнимая ось: это отрезок, идущий из точки B в точку B’, его длина эквивалентна
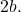
- Асимптоты : пунктирные линии, показанные на графике. Ниже мы увидим, как они рассчитываются.
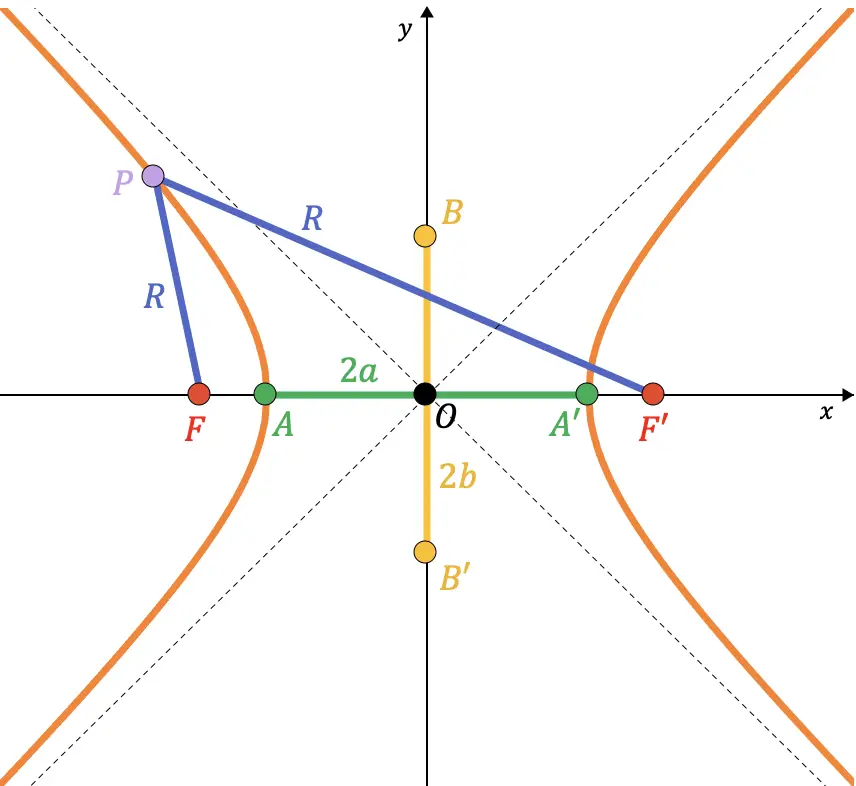
Связь между элементами гиперболы
Прежде всего, мы говорим, что полуось означает половину оси. Например, истинная полуось — это отрезок, идущий от точки А до центра гиперболы, длина которого равна
![]()
Таким образом, существует очень важная связь между реальной полуосью, мнимой полуосью и полуфокусным расстоянием. Фактически, формула, которую мы собираемся вывести дальше, часто используется для решения упражнений и задач с гиперболой.
Следует знать, что точки В и В’ гиперболы соответствуют точкам пересечения главной оси и воображаемой окружности радиуса
![]()
(полуфокусное расстояние) от центра до точки А. Следовательно, как видно на следующем графическом изображении, отрезок, соединяющий точку А и точку В, совпадает с радиусом указанного круга (
![]()
):
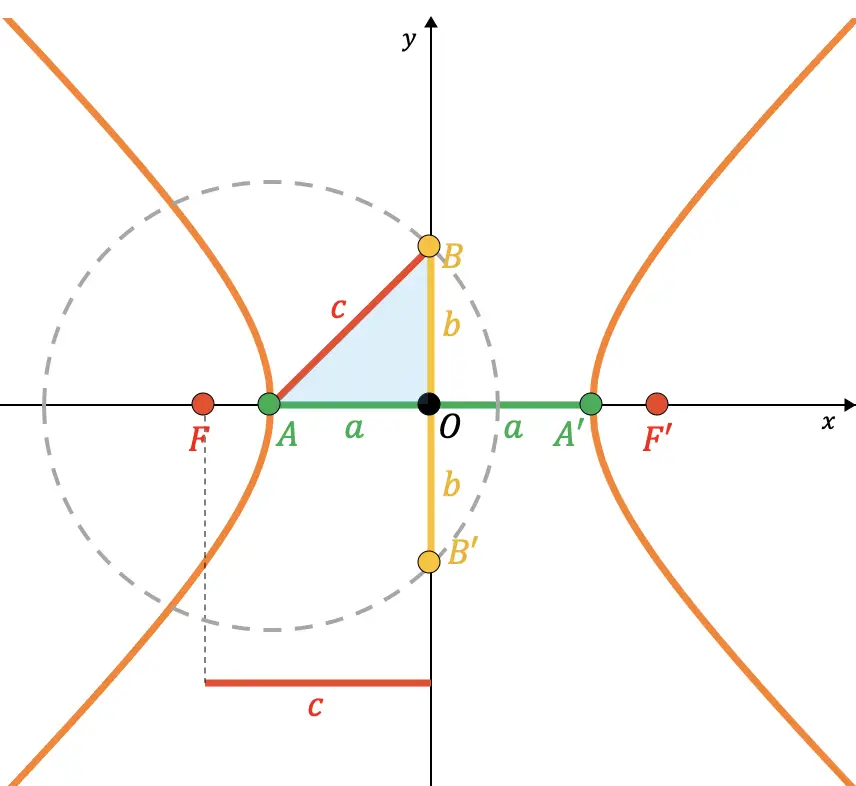
Таким образом, на основе теоремы Пифагора можно продемонстрировать, что связь между параметрами
![]()
И
![]()
следующее:
![]()
уравнение гиперболы
Существует несколько типов уравнений гиперболы, поскольку в зависимости от ее свойств для ее математического выражения используется то или иное. Далее мы разберем каждый подробно.
Во-первых, мы имеем обычное уравнение гиперболы. Во-вторых, мы увидим вариант обычного уравнения, это приведенное или каноническое уравнение гиперболы. Далее мы изучим, как устроено общее уравнение гиперболы. И, наконец, разберем уравнения двух частных случаев гипербол: равносторонней гиперболы и сопряженной гиперболы .
Обычное уравнение гиперболы
Когда мы хотим определить уравнением гиперболу с внешним центром в начале координат (точка (0,0)), мы должны использовать следующую формулу:
Формула обыкновенного уравнения гиперболы в декартовых координатах имеет следующий вид:
![]()
Золото:
-

И

– координаты центра гиперболы:
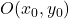
-

— длина большой полуоси гиперболы.
-

— длина малой полуоси гиперболы.
С помощью этого уравнения вы можете описать гиперболы, фокальная ось которых горизонтальна (ветви открыты влево и вправо), чем обычно и являются гиперболы. Но если мы работаем с вертикальной фокальной осью (ветви открываются сверху вниз), отрицательный знак переходит от переменной y к переменной x :
![]()
Золото
![]()
И
![]()
являются, как и прежде, координатами центра гиперболы и членами
![]()
И
![]()
они по-прежнему являются большой полуосью и малой полуосью гиперболы, хотя, в отличие от предыдущего, эти две теперь будут ориентированы вертикально и горизонтально соответственно.
Каноническое или приведенное уравнение гиперболы
Этот тип уравнения гиперболы очень похож на обычное уравнение, с той лишь разницей, что каноническое уравнение используется для аналитического выражения гипербол, центром которых является точка (0,0). Поэтому мы используем каноническое или приведенное уравнение гиперболы, когда центр гиперболы является началом координат.
Выведем теперь формулу приведенного уравнения гиперболы из ее обыкновенного уравнения:
![]()
Если центр гиперболы должен быть началом координат, т.е. точкой (0,0), всегда будет верно следующее:
![]()
![]()
Таким образом, каноническая или сокращенная формула уравнения гиперболы будет иметь вид:
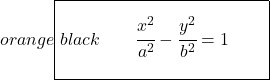
Как и раньше, если бы фокальная ось была вертикальной, а не горизонтальной, отрицательной переменной было бы x :
![]()
Общее уравнение гиперболы
Формула общего уравнения гиперболы имеет следующий вид:
![]()
Однако для того, чтобы приведенное выше уравнение было гиперболой, коэффициенты
![]()
И
![]()
Они должны быть отличны от нуля и в то же время иметь противоположный знак.
Уравнение равносторонней гиперболы
Равносторонняя гипербола – это гипербола, у которой длина действительной полуоси эквивалентна длине мнимой полуоси, это означает, что
![]()
Следовательно, уравнение равносторонней гиперболы имеет вид:
![]()
Кроме того, асимптоты равносторонних гипербол перпендикулярны друг другу. А уравнения этих линий таковы:
![]()
![]()
Если внимательно посмотреть, эти два уравнения представляют собой биссектрисы первого (и третьего) квадранта и второго (и четвертого) квадранта соответственно. Итак, если повернуть равностороннюю гиперболу на 45° влево, ее асимптоты займут место осей координат:
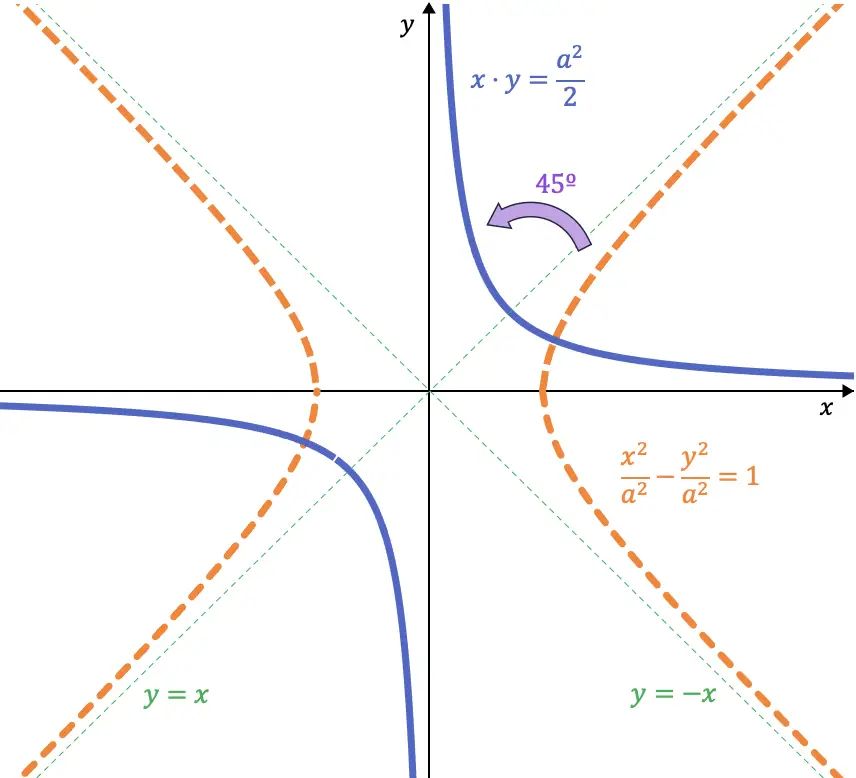
Итак, когда мы делаем поворот на 45°, уравнение гиперболы будет выглядеть так:
![]()
сопряженные гиперболы
Две гиперболы называются сопряженными, если действительная ось одной эквивалентна мнимой оси другой . Поэтому единственная разница между уравнениями двух сопряженных гипербол заключается в том, какая переменная отрицается, ведь коэффициенты при знаменателях должны оставаться прежними.
Вот пример уравнений двух гипербол, сопряженных друг другу:
![]()
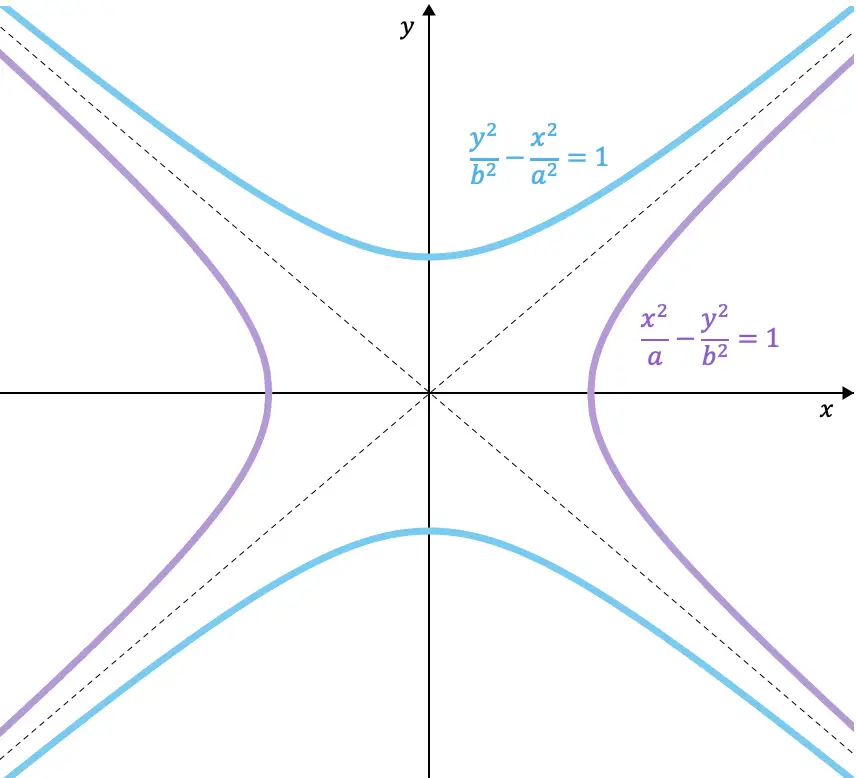
Кроме того, как вы можете видеть из изображенных на графике гипербол, сопряженные гиперболы имеют одни и те же асимптоты.
Асимптоты гиперболы
Как вы видели на предыдущих графиках, каждая гипербола имеет две асимптоты. Помните, что асимптота — это прямая линия, которая очень близко приближается к функции, но никогда полностью не пересекает и не касается ее.
Итак, формулы, соответствующие асимптотам гипербол:
![]()
![]()
Так что асимптоты любой гиперболы можно легко определить с помощью ее коэффициентов
![]()
И
![]()
которые являются соответственно длинами действительной полуоси и мнимой полуоси гиперболы.
Эксцентриситет гиперболы
Эксцентриситет гиперболы — характерный параметр, определяющий, насколько она открыта или закрыта. Численно эксцентриситет гиперболы рассчитывается путем деления ее полуфокусного расстояния на ее действительную полуось:
![]()
Эксцентриситет любой гиперболы всегда больше 1:
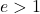
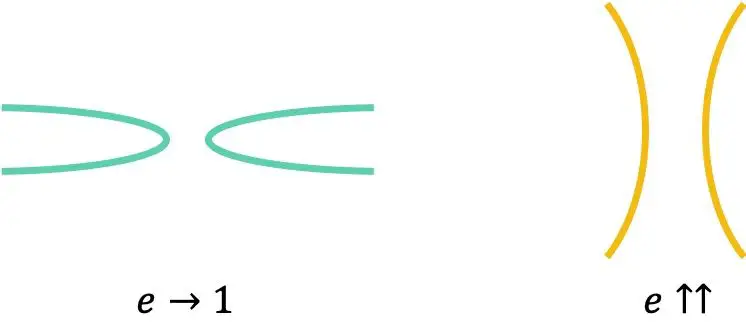
Наконец, следует отметить, что эксцентриситет равносторонней гиперболы всегда равен
![]()
Решены задачи с гиперболой
Ниже вы можете попрактиковаться в изученных нами концепциях с помощью задач и решений упражнений с гиперболами и уравнением гиперболы.
Упражнение 1
Каково уравнение гиперболы с центром в точке (-1,3), длиной действительной полуоси 3 единицы и длиной мнимой полуоси (параллельной оси Y) 7 единиц?
Чтобы найти уравнение гиперболы, просто примените формулу обычного уравнения гиперболы:
![]()
Подставим координаты центра гиперболы в уравнение:
![]()
![]()
И наконец, подставляем значения неизвестных
![]()
И
![]()
![]()
![]()
Упражнение 2
Найдите координаты центра, вершин, фокусов, значение эксцентриситета и асимптоты гиперболы, уравнение которой определяется формулой:
![]()
Прежде всего следует отметить, что отрицательной переменной в уравнении является переменная y , поэтому ветви гиперболы будут открываться вправо и влево (фокальная ось параллельна оси X).
Во-вторых, уравнение соответствует каноническому (или приведенному) уравнению гиперболы, поэтому его центр является началом координат.
![]()
Зная центр гиперболы, для расчета всего остального нам нужно найти значение реальной полуоси (параметр
![]()
) и мнимую полуось (параметр
![]()
). И то, и другое мы можем вывести из формулы канонического (или приведенного) уравнения гиперболы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Итак, если между центром и вершинами есть расстояние в 5 единиц, это означает, что вершины гипербол:
![]()
Для определения координат каждой точки фокуса необходимо знать значение половины фокусного расстояния (параметр
![]()
). И для этого мы можем использовать формулу, соединяющую элементы гиперболы:
![]()
![]()
![]()
Таким образом, между центром и домами имеется пространство в 13 квартир. Таким образом, координаты каждого домохозяйства таковы:
![]()
Тогда для расчета эксцентриситета гиперболы нам нужно воспользоваться соответствующей ей формулой:
![]()
И, наконец, находим асимптоты гиперболы по их формулам:
![]()
![]()
Упражнение 3
Рассчитайте уравнение гиперболы с центром в начале координат, зная, что разница расстояний от точки гиперболы до фокусов F(-4,0) и F(4,0) составляет 6 единиц.
Во-первых, поскольку гипербола имеет центр в начале координат, мы воспользуемся каноническим или приведенным уравнением:
![]()
Тогда, согласно определению гиперболы, абсолютная величина разности расстояний от одной из ее точек до фокусов (которая в данном случае равна 6) должна быть равна длине вещественной оси (
![]()
). Еще:
![]()
![]()
![]()
![]()
С другой стороны, центром гиперболы является точка (0,0), а фокусом — точка (4,0). Чтобы расстояние до двух точек (параметр
![]()
) — 4 единицы.
![]()
Теперь мы можем узнать значение параметра
![]()
с математической связью между тремя характеристическими коэффициентами гиперболы:
![]()
![]()
![]()
![]()
Итак, уравнение гиперболы:
![]()
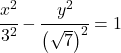
![]()