В этом разделе мы увидим , как обсуждать и решать систему уравнений методом Гаусса-Жордана . То есть определите, является ли это определенно совместимой системой (DCS), неопределенно совместимой системой (ICS) или несовместимой системой. Кроме того, вы найдете примеры и решенные упражнения, которые помогут вам идеально попрактиковаться и усвоить концепции.
Чтобы понять, что мы собираемся объяснить дальше, важно, чтобы вы уже знали, как решать систему с помощью метода Гаусса , поэтому мы рекомендуем вам взглянуть, прежде чем продолжить.
Совместимые системы, определяемые методом Гаусса
Пока последняя строка матрицы Гаусса равна
![]()
, быть
![]()
И
![]()
любые два числа, это SCD (определена совместимость системы). Следовательно, система имеет единственное решение .
Подавляющее большинство систем являются SCD.
Пример:
Например, у нас есть такая система:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
Чья расширенная матрица:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Чтобы решить систему, нам нужно подействовать на строки матрицы и преобразовать все элементы ниже главной диагонали в 0. Итак, из второй строки мы вычитаем первую строку, а из третьей строки мы вычитаем первую строку, умноженную на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Как только все числа ниже главной диагонали равны 0, мы возвращаемся, чтобы преобразовать систему в форму уравнения:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Значит эта система SCD , так как матрица сдвинута и последняя строка имеет тип
![]()
. Поэтому решаем как всегда: исключая неизвестные из уравнений снизу вверх.
![]()
![]()
![]()
Теперь, когда мы знаем z, мы подставляем его значение во второе уравнение, чтобы найти значение
![]()
:
![]()
![]()
![]()
![]()
![]()
И, наконец, делаем то же самое с первым уравнением: подставляем значения остальных неизвестных и решаем
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()
Несовместимые системы по методу Гаусса
Когда в матрице Гаусса у нас есть строка с тремя нулями подряд и числом
![]()
, это ИС (Несовместимая Система), и, следовательно, система не имеет решения .
Пример:
Например, представьте, что после работы с матрицей Гаусса системы у нас осталось:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Поскольку последняя строка
![]()
, то есть три нуля, за которыми следует число в конце, является ЕСЛИ (несовместимая система), и, следовательно, система не имеет решения .
Хоть это и не обязательно знать, ниже вы увидите, почему у нее нет решения.
Если мы возьмем последнюю строку, мы получим следующее уравнение:
![]()
Это уравнение никогда не будет выполнено, потому что какое бы значение ни приняло z , умножение его на 0 никогда не даст 2 (любое число, умноженное на 0, всегда дает 0). А поскольку это уравнение никогда не будет выполняться, система не имеет решения.
Совместимые системы, не определенные методом Гаусса
Всякий раз, когда строка матрицы Гаусса заполняется значением 0
![]()
, это SCI (неопределенная совместимая система), и, следовательно, система имеет бесконечные решения .
Давайте посмотрим пример решения ICS:
Пример:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Как всегда, сначала делаем расширенную матрицу системы :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Теперь мы хотим, чтобы все числа ниже главной диагонали были равны 0. Итак, ко второй строке добавляем первую строку, умноженную на -2:
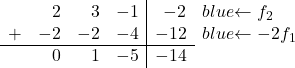
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
Чтобы преобразовать 3 в 0, в третьей строке добавляем первую строку, умноженную на -3:
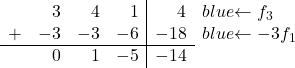
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Чтобы преобразовать 1 в последней строке в 0, в третьей строке мы добавляем вторую строку, умноженную на -1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Поскольку в последней строке все 0 , мы можем удалить ее:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
А поскольку у нас вся строка заполнена нулями, это SCI.
Таким образом, мы получаем следующую систему:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Когда система является SCI, необходимо взять значение параметра из неизвестного
![]()
. И нам нужно решить систему по этому параметру
![]()
.
Поэтому мы присваиваем значение
![]()
до Я :
![]()
Хотя мы могли бы также выбрать любое другое неизвестное в качестве значения
![]()
.
Теперь мы выделим y из второго уравнения и позволим ему быть функцией
![]()
:
![]()
![]()
![]()
И, наконец, мы удаляем x из первого уравнения и также оставляем его как функцию
![]()
:
![]()
![]()
![]()
![]()
Таким образом, системные решения:
![]()
Как видите, в системе SCI мы оставляем решения в зависимости от параметра
![]()
. И помните, что она имеет бесконечные решения, потому что в зависимости от значения, которое она принимает
![]()
, решение будет одно или другое.
Прежде чем перейти к решаемым упражнениям, следует знать, что хотя в этой статье мы используем метод Гаусса, другим способом обсуждения и решения систем линейных уравнений является теорема Руша . На самом деле, его, вероятно, используют больше.
Решенные упражнения по обсуждению систем уравнений методом Гаусса-Жордана.
Упражнение 1
Определите, о каком типе системы идет речь, и решите следующую систему уравнений, используя метод Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
Первое, что нам нужно сделать, это расширенную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Теперь нам нужно сделать все числа ниже основного массива равными 0.
Поэтому мы выполняем операции со строками, чтобы отменить два последних члена первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
Мы получили строку матрицы, состоящую из трех нулей, за которыми следует число. Следовательно, это IS (несовместимая система), и система не имеет решения.
Упражнение 2
Определите, что это за система, и найдите решение следующей системы уравнений с помощью метода Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
Первое, что нам нужно сделать, это расширенную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Теперь нам нужно сделать все числа ниже основного массива равными 0.
Поэтому мы выполняем операции со строками, чтобы отменить два последних члена первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Теперь попробуем удалить последний элемент из второго столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Но мы получаем целый ряд нулей. Итак, это SCI , и система имеет бесконечно много решений.
Но поскольку это ИСУ, мы можем решить систему на основе
![]()
. Поэтому мы удаляем строку 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
Теперь выразим матрицу в виде системы уравнений с неизвестными:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
Мы даем значение
![]()
Для
![]()
![]()
Заменяем значение
![]()
во втором уравнении найти значение
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и стираем
![]()
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()
Упражнение 3
Найдите, что это за система, и решите следующую систему уравнений методом Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
Первое, что нам нужно сделать, это расширенную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Применить метод Гаусса проще, если первое число в первой строке равно 1. Поэтому мы изменим порядок строк 1 и 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Теперь нам нужно сделать все числа ниже основного массива равными 0.
Поэтому мы выполняем операции со строками, чтобы отменить два последних члена первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Теперь преобразуем последний элемент второго столбца в ноль:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Эта система является SCD , так как нам удалось сдвинуть матрицу и последняя строка имеет тип
![]()
. Следовательно, оно будет иметь единственное решение.
Когда все числа ниже главной диагонали равны 0, мы можем решить систему уравнений. Для этого еще раз выразим матрицу в виде системы уравнений с неизвестными:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
И решаем неизвестные уравнения снизу вверх. Сначала решим последнее уравнение:
![]()
![]()
Теперь подставим значение z во второе уравнение, чтобы найти значение y:
![]()
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и находим x:
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()
Упражнение 4
Определите, к какому типу относится система, и решите методом Гаусса следующую систему уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
Первое, что нам нужно сделать, это расширенную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Теперь нам нужно сделать все числа ниже основного массива равными 0.
Поэтому мы выполняем операции со строками, чтобы отменить два последних члена первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Теперь попробуем удалить последний элемент из второго столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Но мы получаем целый ряд нулей. Итак, это SCI , и система имеет бесконечно много решений.
Но поскольку это ИСУ, мы можем решить систему на основе
![]()
. Поэтому мы удаляем строку 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
Теперь выразим матрицу в виде системы уравнений с неизвестными:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
Мы даем значение
![]()
Для
![]()
![]()
Заменяем значение
![]()
во втором уравнении найти значение
![]()
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и стираем
![]()
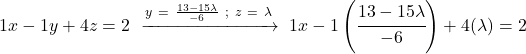
![]()
![]()
У нас есть сумма с дробями. Поэтому приведем все слагаемые к общему знаменателю:
![]()
![]()
Поскольку теперь все они имеют одинаковый знаменатель, мы можем сгруппировать их в одну дробь:
![]()
И, наконец, работаем с числителем:
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()