В этой статье мы объясним, как сохранить предел функции, когда она дает неопределенность 0/0. Кроме того, вы сможете попрактиковаться с решенными упражнениями на неопределенность нуля между нулями.
Как решить нулевую неопределенность между нулем (0/0)
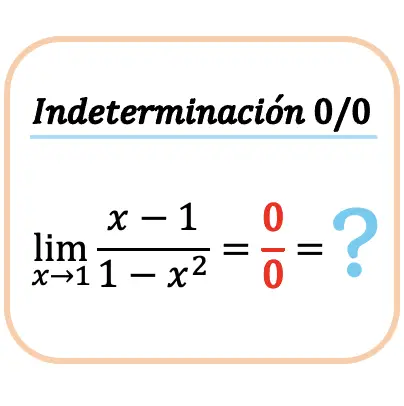
Затем мы увидим, как вычислить предел функции, когда она дает нулевую неопределенность между нулем (0/0). Для этого пошагово рассчитаем пример:
Сначала мы попытаемся вычислить предел, подставив значение x в функцию:
Но мы получаем неопределенность 0, разделенную на 0.
Когда предел точечной функции дает неопределенность 0/0 , необходимо факторизовать полиномы числителя и знаменателя, а затем упростить общие множители.
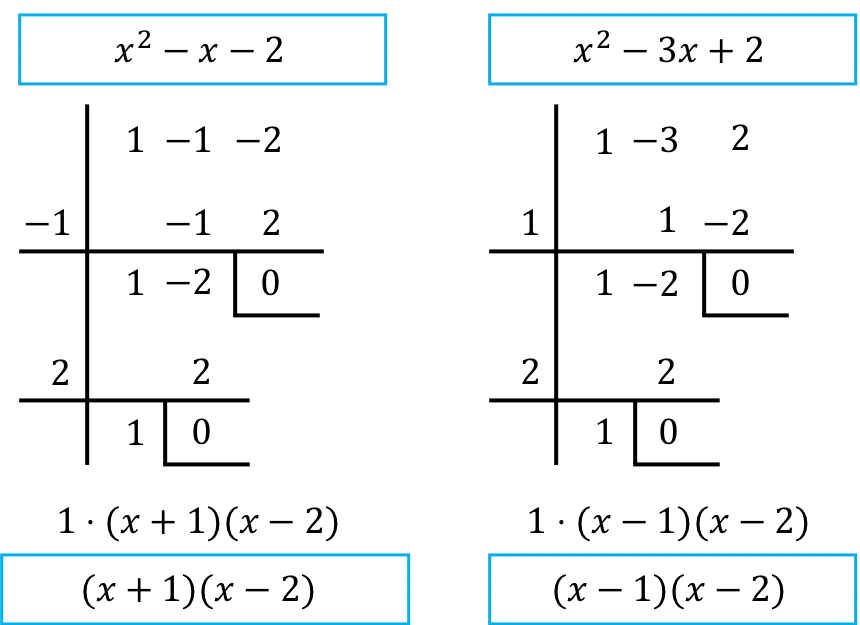
Поэтому мы должны факторизовать полиномы числителя и знаменателя дроби. Для этого воспользуемся правилом Руффини:
➤ Если вы не знаете , как факторизовать полином , рекомендуем посмотреть объяснение на нашем сайте, специализирующемся на полиномах: www.polinomios.org
Таким образом, после факторизации полиномов предел будет следующим:
Теперь мы можем упростить предел, исключив множители, повторяющиеся в числителе и знаменателе дроби:
И наконец, пересчитываем лимит:
Как видите, если мы факторизуем и упрощаем многочлены, то найти решение в пределе очень легко.
Неопределенность 0/0 с корнями
Мы только что видели, как разрешаются неопределенности 0/0 рациональных функций. Однако, если предел имеет иррациональную (или радикальную) функцию, неопределенность 0/0 разрешается иначе.
Сначала мы пытаемся разрешить лимит, выполнив следующие операции:
Но мы получаем нулевую неопределенность.
Если предел функции с корнями дает неопределенность 0/0 , необходимо умножить числитель и знаменатель дроби на сопряженное подкоренное выражение.
➤ Помните, что сопряженное — это то же иррациональное выражение, но с измененным средним знаком.
Далее умножаем числитель и знаменатель дроби на сопряженное подкоренное выражение:
В рамках этого типа ограничений, выполняя этот шаг, мы всегда получим заметную идентичность, которую можно упростить. В данном случае в знаменателе мы имеем произведение суммы и разности, следовательно:
Упростим множитель, который повторяется в числителе и знаменателе:
И таким образом мы можем найти результат предела:
Решенные упражнения на неопределенность 0/0
Ниже мы подготовили несколько пошаговых упражнений на пределы функций, дающих неопределенности 0/0. Вы можете попробовать выполнить их, а затем проверить решение.
Не забывайте, что любые вопросы по поводу разрешения лимитов вы можете задать нам в комментариях!
Упражнение 1
Вычислите предел следующей рациональной функции в точке x=-2.
Логично, что сначала мы пытаемся решить предел:
Но в итоге мы получаем неопределенность 0/0. Поэтому мы должны факторизовать полиномы числителя и знаменателя:
Теперь упростим дробь, убрав круглые скобки, повторяющиеся в числителе и знаменателе:
И, наконец, пересчитываем предел с помощью упрощенной дроби:
Упражнение 2
Решите предел следующей функции, когда x приближается к -1:
Сначала мы пытаемся разрешить лимит как обычно:
Но мы получаем неопределенность 0 между 0. Поэтому мы должны факторизовать 2 многочлена дроби:
Теперь мы можем упростить полиномы:
И решаем предел:
Упражнение 3
Определите решение предела следующей радикальной функции:
Сначала проверяем, дает ли предел какую-то неопределенность:
Предел дает ноль неопределенности, разделенный на ноль, и мы имеем корень в функции. Поэтому мы должны умножить числитель и знаменатель дроби на сопряженное радикальное выражение:
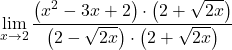
Знаменатель соответствует развитию заметной идентичности произведения суммы и разности, поэтому мы можем его упростить:
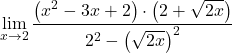
Однако мы пока не можем упростить условия дроби. Поэтому мы должны факторизовать полиномы:
Таким образом, мы можем упростить дробь:
И теперь мы можем определить результат лимита:
Упражнение 4
Рассчитайте предел следующей радикальной функции при приближении x к 0:
Сначала попытаемся вычислить предел функции, как мы всегда это делаем:
Но мы получаем неопределенную форму 0/0. Поэтому умножаем числитель и знаменатель функции на сопряженное иррациональному выражению:
Мы применяем соответствующую примечательную формулу тождества, чтобы упростить знаменатель:
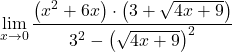
Теперь факторизуем бином числителя, взяв общий множитель:
![\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1a55c3d856552106a7f81eb9bcc6eff_l3.png "Rendered by QuickLaTeX.com")
Упростим множители, которые повторяются в числителе и знаменателе функции:
И, наконец, решаем предел функции:
![\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b4874df2f48ad131d48c4e5923a5b02_l3.png "Rendered by QuickLaTeX.com")
Упражнение 5
Решите следующий предел, используя метод неопределенности 0/0:
➤ См.: как вычислить боковые пределы функции
Сначала мы пытаемся разрешить предел:
Но в пределе мы получаем неопределенность нуль на нуле. Поэтому факторизуем многочлены числителя и знаменателя:
Теперь упростим дробь, исключив множители, повторяющиеся в числителе и знаменателе:
И снова вычисляем лимит:
Но теперь мы столкнулись с неопределенностью числа, деленного на 0. Поэтому мы должны вычислить боковые пределы функции, когда x стремится к -1.
Сначала мы находим боковой предел функции в точке x=-1 слева:
А затем вычисляем боковой предел функции в точке x=-1 справа:
Следовательно, поскольку два боковых предела не совпадают, предела функции при x=-1 не существует:
