Неявное, общее или декартово уравнение плоскости

Объяснение того, как рассчитывается неявное уравнение плоскости (формула), также известное как общее или декартово уравнение. Дополнительно вы узнаете, как найти уравнение плоскости по вектору ее нормали. Более того, вы сможете увидеть примеры и упражнения, решаемые шаг за шагом.

Каково неявное или общее уравнение плана?

В аналитической геометрии неявное уравнение плоскости , также называемое общим или декартовым уравнением плоскости, представляет собой уравнение, которое позволяет математически выразить любую плоскость. Чтобы найти неявное или общее уравнение плоскости, нам нужна точка и два линейно независимых вектора, принадлежащих этой плоскости.

Формула неявного или общего уравнения плана

Рассмотрим точку и два направляющих вектора плоскости:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Неявное, общее или декартово уравнение плоскости получается путем решения следующего определителя и присвоения результата, равного 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Таким образом, неявное или общее уравнение полученного плана будет следующим:

$Ax+By+Cz+D=0$

Важно, что два вектора в формуле линейно независимы друг от друга, то есть должны иметь разные направления. И чтобы это условие выполнялось, достаточно, чтобы два вектора не были параллельны.

неявное или общее или декартово уравнение pan xy в r3

Хотя нет необходимости знать причину этой формулы, вы можете увидеть ее демонстрацию ниже.

Отталкиваясь от параметрических уравнений плана, перейдем к неявному (или общему) уравнению плана:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Сначала мы передаем независимый член из каждого параметрического уравнения в другую часть уравнения:

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Или эквивалент:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Чтобы приведенная выше система уравнений имела допустимое решение, ранг следующей матрицы должен быть равен 2 (теорема Руша-Фробениуса):

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Таким образом, если диапазон предыдущей матрицы должен быть равен двум, определитель 3×3 обязательно должен быть равен нулю:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

И решив этот определитель, мы получаем общее, неявное или декартово уравнение плоскости:

$Ax+By+Cz+D=0$

Итак, мы только что рассмотрели неявное (или общее) уравнение и параметрические уравнения плоскости, однако существует еще больше способов аналитического выражения плоскости, например векторное уравнение и каноническое уравнение. Формулу и объяснение всех уравнений плана вы можете посмотреть по этой ссылке.

Пример того, как найти неявное или общее уравнение плоскости

Давайте посмотрим, как определить неявное (или общее, или декартово) уравнение плоскости на примере:

Найдите неявное или общее уравнение плоскости, проходящей через точку.
$P(3,1,-1)$

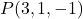
и содержит векторы

$\vv{\text{u}}=(2,0,3)$

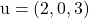
И

$\vv{\text{v}}=(4,-1,2).$

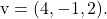
Чтобы вычислить общее или неявное уравнение плоскости, необходимо решить следующий определитель, образованный двумя векторами, переменными и координатами точки:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Итак, подставляем векторы и точку в формулу:

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

А теперь решаем определитель 3-го порядка, например, по правилу Сарруса или по кофакторам (или заместителям):

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Теперь оперируем и группируем термины:

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Следовательно, неявное или общее уравнение плана таково:

$\bm{3x+8y-2z-19 = 0}$

Вычислить неявное или общее уравнение плоскости по вектору нормали.

Очень типичная задача в уравнениях плоскости — найти, как выглядит уравнение данной плоскости с учетом точки и ее нормального (или перпендикулярного) вектора. Итак, давайте посмотрим, как это работает.

Но прежде всего необходимо знать, что компоненты X, Y, Z вектора нормали к плоскости совпадают соответственно с коэффициентами A, B, C неявного (или общего) уравнения этой плоскости.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Золото

$\vv{n}$

вектор, ортогональный плоскости

$\pi.$

Как только мы узнаем предыдущее соотношение, давайте посмотрим пример решения такого типа задач с уравнением плоскости:

Определите неявное или общее уравнение плоскости, проходящей через точку.
$P(1,0,-2)$

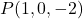
и один из его нормальных векторов есть

$\vv{n}=(3,-1,2) .$

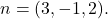
Формула неявного, общего или декартова уравнения плоскости:

$Ax+By+Cz+D=0$

Таким образом, из вектора нормали мы можем найти коэффициенты A, B и C, поскольку они эквивалентны компонентам его вектора нормали:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Пока нам нужно найти только параметр D. Для этого подставим в уравнение координаты точки, принадлежащей плоскости:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

Таким образом, неявное или общее уравнение плана таково:

$\bm{3x-y+2z+1 = 0}$

Решаемые задачи неявного или общего уравнения плоскости

Упражнение 1

Найдите неявное или общее уравнение плоскости, проходящей через точку.

$P(-2,1,3)$

и содержит векторы

$\vv{\text{u}}=(4,1,3)$

$\vv{\text{v}}=(5,3,-1).$

посмотреть решение

Чтобы вычислить общее или неявное уравнение плоскости, необходимо решить следующий определитель, образованный двумя векторами, тремя переменными и координатами точки:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Итак, подставляем векторы и точку в формулу:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

А теперь решаем определитель матрицы 3×3 выбранным вами методом:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Наконец, выполняем операции и группируем подобные члены:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Таким образом, неявное или общее уравнение плана таково:

$\bm{-8x+11y+7z-20 = 0}$

Упражнение 2

Определите, является ли точка

$P(-1,5,-3)$

принадлежит следующему плану:

$\pi : \ 2x+y+6z-5=0$

посмотреть решение

Чтобы точка находилась в плоскости, необходимо проверить ее уравнение. Поэтому нам нужно подставить декартовы координаты точки в уравнение плоскости и проверить, выполняется ли уравнение:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

Точка не подчиняется уравнению плоскости, поэтому она не является частью этой плоскости.

Упражнение 3

Найдите неявное (или общее) уравнение плана, содержащее следующие три точки:

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

посмотреть решение

Чтобы найти неявное уравнение плоскости, нам нужно найти два линейно независимых вектора, которые связаны на плоскости. И для этого мы можем вычислить два вектора, которые определяются тремя точками:

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

Координаты двух найденных векторов не пропорциональны, поэтому они фактически линейно независимы друг от друга.

Теперь мы уже знаем два направляющих вектора и одну точку плоскости, поэтому уже можем применить формулу общего уравнения плоскости:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Подставим в формулу векторы и одну из трёх точек:

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$