Неопределенность бесконечная минус бесконечность (∞-∞)

В этой статье мы объясняем, как решить бесконечную минус бесконечную (∞-∞) неопределенность. Вы найдете примеры этой неопределенности с различными типами функций и, кроме того, сможете попрактиковаться в упражнениях, решающих шаг за шагом неопределенность бесконечность минус бесконечность.

Решение неопределенности: бесконечность минус бесконечность

Когда предел функции дает бесконечность минус бесконечность, это означает, что это неопределенность (или неопределенная форма). То есть предел функции, дающей неопределенность минус бесконечность, не может быть определен путем выполнения прямого вычисления, а должна быть проведена предварительная процедура.

Поэтому, чтобы решить бесконечность минус бесконечная неопределенность, мы должны сначала применить процедуру, которая зависит от типа функции: если это полиномиальная функция, ее можно вычислить путем сравнения, если это рациональная функция, дроби необходимо привести к общий знаменатель, и если это иррациональная функция, ее необходимо умножить на сопряженную.

\displaystyle\lim_{x\to+\infty}\Bigl(f(x)-g(x)\Bigr)=\infty-\infty

Далее мы увидим на примерах, как неопределенность «бесконечная минус бесконечность» разрешается в каждом типе функций.

Бесконечная минус бесконечная неопределенность в полиномиальных функциях

В полиноме неопределенность бесконечность минус бесконечность равна бесконечности высшего порядка, то есть член высшего порядка определяет положительный или отрицательный знак бесконечности.

Например, посмотрите на предел следующей полиномиальной функции, которая дает неопределенную форму бесконечность минус бесконечность:

\displaystyle\lim_{x\to+\infty}\bigl(x^2-3x\bigr)=(+\infty)^2-3\cdot (\infty)=+\infty-\infty=+\infty

В этом случае член x 2 имеет вторую степень, а член 3x — первую степень, поэтому моном x 2 является доминирующим, поскольку он имеет более высокий порядок. Следовательно, результатом предела является бесконечность, полученная из этого члена.

Взгляните на другие примеры:

\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}

Короче говоря, когда мы делаем пределы до бесконечности в полиномиальных функциях , мы должны просто подставить бесконечность в член высшей степени , игнорируя все остальные члены.

Неопределенность бесконечная минус бесконечность с дробями

Когда неопределенность бесконечность минус бесконечность возникает при сложении или вычитании алгебраических дробей , мы должны сначала выполнить сложение или вычитание дробей, а затем вычислить предел.

Давайте посмотрим, как вычислить неопределенность бесконечность минус бесконечность в функции с дробями, пошагово решив пример:

\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)

Давайте сначала попробуем вычислить лимит:

\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}

Но мы получаем неопределенность ∞-∞.

Итак, сначала нам нужно заняться вычитанием дробей. Для этого приведем дроби к общему знаменателю, то есть умножим числитель и знаменатель одной дроби на знаменатель другой:

\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}

И теперь, когда обе дроби имеют одинаковый знаменатель, мы можем объединить их в одну дробь:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}

Действуем в числителе и знаменателе:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}

И, наконец, снова вычисляем лимит:

\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}

В этом случае бесконечная неопределенность между бесконечностью дает +∞, поскольку степень числителя больше степени знаменателя.

➤ Смотрите: что такое бесконечность между бесконечностью?

неопределенность бесконечный минус бесконечный с корнями

Когда неопределенность бесконечность минус бесконечность возникает при радикальном сложении или вычитании , мы должны сначала умножить и разделить функцию на сопряженное радикальное выражение, а затем найти предел.

Мы увидим, как решить неопределенность бесконечность минус бесконечность в иррациональной функции, на пошаговом примере:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)

Давайте сначала попробуем решить предел функции с радикалами:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}

Однако мы получаем неопределенную форму ∞-∞. Итак, чтобы узнать, сколько неопределенности составляет бесконечность минус бесконечность, нам нужно применить объясненную процедуру.

Поскольку функция имеет радикалы, умножим и разделим всю функцию на сопряженное иррациональное выражение:

\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}

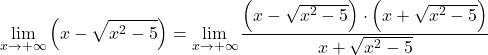
Алгебраическое выражение числителя соответствует заметному тождеству произведения суммы на разность, поэтому мы можем упростить выражение:

\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}

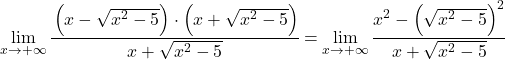
Теперь упростим корень предела, поскольку он возведён в квадрат:

\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}

Оперируем числителем дроби:

\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}

И наконец, переделываем расчет лимита:

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}

Таким образом, результат предела равен 0, поскольку любое число, разделенное на бесконечность, равно нулю.

Решены проблемы бесконечности минус бесконечности неопределенности

Упражнение 1

Решите следующий предел при приближении x к бесконечности:

\displaystyle\lim_{x\to +\infty}(7x^2-2x^3)

В этом пределе член высшего порядка имеет третью степень, поэтому мы ориентируемся на бесконечность, полученную из этого члена.

\displaystyle\lim_{x\to +\infty}(+7x^2-2x^3)=+\infty^2-\infty^3=+\infty-\infty=\bm{-\infty}

Упражнение 2

Вычислите предел следующей полиномиальной функции, когда x приближается к отрицательной бесконечности:

\displaystyle\lim_{x\to -\infty}(-5x^3-9x^2)

Отрицательная бесконечность в кубе остается отрицательной, но в квадрате становится положительной. позже Хотя их знаки изменяются коэффициентами перед ними:

\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}

Тогда неопределенная форма бесконечность минус бесконечность определяется членом высшего порядка (-5x 3 ), из которого мы получаем положительную бесконечность:

\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\bm{+\infty}

Упражнение 3

Определите предел до бесконечности следующей рациональной функции:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)

Сначала попытаемся вычислить предел, заменив бесконечность в функции:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}

Но в итоге мы получаем неопределенность ∞ – ∞. Поэтому приведем дроби к общему знаменателю:

\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}

А поскольку обе дроби теперь имеют одинаковый знаменатель, мы можем объединить их в одну дробь:

\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}

Заключаем скобки числителя:

\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}

И, наконец, определяем предел:

\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}

В этом случае неопределенность ∞/∞ дает +∞, поскольку степень числителя больше степени знаменателя.

Упражнение 4

Решите предел следующей дробной функции, когда x приближается к 0:

\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)

Сначала попробуем вычислить лимит как обычно:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}

Но мы получаем неопределенную форму ∞-∞. Следовательно, нам необходимо привести дроби функции к общему знаменателю.

В данном случае х 4 кратно х 2 , поэтому простым умножением числителя и знаменателя второй дроби на х 2 получим, что обе дроби имеют одинаковый знаменатель:

\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}

Теперь мы можем вычесть две дроби:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}

Пробуем разрешить лимит еще раз:

\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}

Но в итоге мы получаем неопределенность константы, разделенной на ноль. Поэтому необходимо вычислить боковые пределы функции.

\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

В заключение, поскольку два боковых предела функции в точке x=0 дают -∞, решение предела есть -∞:

\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}

Упражнение 5

Решите предел до бесконечности следующей функции с корнями:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)

Пытаясь решить предел, получаем неопределенность бесконечность минус бесконечность:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}

Следовательно, поскольку в функции есть радикалы, нам нужно ее умножить и разделить на выражение сопряженного радикала:

\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}

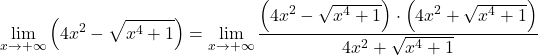
В числителе мы имеем примечательное произведение суммы на разность, равную разнице квадратов. Еще:

\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}

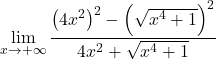
Упрощаем радикал до квадрата:

\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}

Действуем в числителе:

\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}

И, наконец, находим предел:

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}

В этом случае бесконечная неопределенность, разделенная на бесконечность, является более бесконечной, поскольку степень числителя больше степени знаменателя (напомним, что квадратный корень уменьшает степень на два:

\sqrt{x^4} = x^{4/2} = x^2

).

Упражнение 6

Решите предел при стремлении x к бесконечности следующей иррациональной функции:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)

Сначала попробуем вычислить лимит как обычно:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}

Но оно дает нам в результате неопределенность разности бесконечностей. Следовательно, поскольку функция имеет корни, нам нужно умножить и разделить выражение на сопряженный радикал:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}

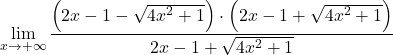
Сгруппируем примечательное равенство числителя дроби:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}

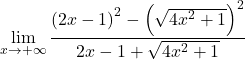
Решаем квадратный корень:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Решаем примечательное тождество квадрата разности:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Действуем в числителе:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}

\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}

И, наконец, вычисляем значение предела на бесконечности:

\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =

Несмотря на то, что в знаменателе стоит квадрат х, на самом деле его степень равна 1, поскольку он находится внутри корня:

\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .

Следовательно, результатом неопределенности -∞/+∞ является деление коэффициентов при х более высокой степени, поскольку степень числителя равна степени знаменателя.

\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}

Заметим, что поскольку в знаменателе имеются два члена первой степени

\bigl(2x

И

\sqrt{4x^2}\bigr)

, чтобы разрешить неопределенность -∞/+∞, необходимо взять все коэффициенты членов первой степени, то есть

2

из

2x

и

\sqrt{4}

из

\sqrt{4x^2}.

Упражнение 7

Рассчитайте предел при приближении x к 1 следующей функции с дробями:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)

Пытаясь сделать предел, мы получаем неопределенный предел бесконечности минус бесконечность:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}

Поэтому мы должны привести дроби к общему знаменателю, или, другими словами, мы должны умножить числитель и знаменатель одной дроби на знаменатель другой:

\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}

И поскольку теперь обе дроби имеют одинаковый знаменатель, мы можем сложить их вместе:

\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}

Мы работаем:

\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}

\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}

И мы снова пытаемся решить предел:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}

Но мы находим ноль неопределенности, разделенный на ноль. Поэтому мы должны факторизовать полиномы числителя и знаменателя:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}

Теперь упростим дробь, убрав множитель, повторяющийся в числителе и знаменателе:

\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}

И, наконец, решаем предел:

\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх