Наклон линии (формула)

На этой странице вы найдете наиболее подробное объяснение наклона линии: какова ее формула, примеры расчета, что означает понятие наклона линии… Вы также сможете увидеть, как легко определить наклон линии. линии из ее уравнения и, кроме того, вы сможете попрактиковаться, выполняя упражнения, решаемые шаг за шагом.

Формула наклона линии

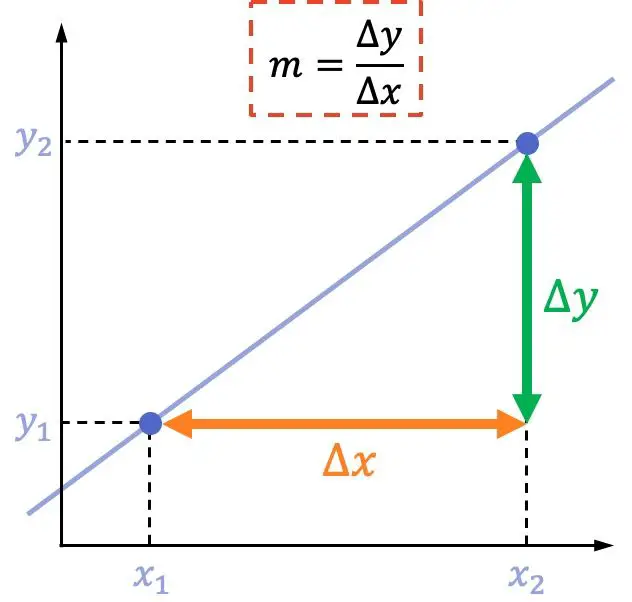
Наклон линии равен вертикальному смещению между двумя точками, деленному на горизонтальное смещение между этими двумя точками.

То есть, учитывая две точки на прямой:

$P_1(x_1,y_1) \qquad P_2(x_2,y_2)$

Формула наклона линии:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Пример расчета наклона линии из двух точек

Далее мы увидим пример того, как рассчитывается наклон линии по формуле:

Рассчитайте наклон линии, проходящей через следующие две точки:

$P_1(3,1) \qquad P_2(5,7)$

Чтобы найти наклон этой линии, просто примените ее формулу:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{7-1}{5-3}=\cfrac{6}{2} = \bm{3}$

Таким образом, наклон линии равен 3.

Нахождение наклона прямой по ее уравнению

В разделе выше мы только что увидели, как численно определить наклон линии. Однако не всегда необходимо производить расчеты, но ее значение можно определить и из уравнения линии. Каждый тип уравнения различен, поэтому мы разберем каждый случай отдельно.

Наклон по явному уравнению линии

Явное уравнение линии следует следующему выражению:

$y =\color{blue}\bm{m}\color{black}x+n$

Тогда параметр

$m$

соответствует наклону линии.

Наклон с учетом уравнения наклона точки линии.

Формула уравнения точки-наклона линии выглядит следующим образом:

$y -y_0=\color{blue}\bm{m}\color{black}(x-x_0)$

Как и ранее, коэффициент

$m$

соответствует наклону линии.

Наклон с учетом неявного уравнения линии

Учитывая неявное уравнение линии (также называемое общим или декартовым уравнением):

$Ax+By+C=0$

Наклон линии можно найти, выполнив:

$m=-\cfrac{A}{B}$

Наклон с учетом вектора направления линии

Вектор направления линии — это вектор, обозначающий ее направление. Итак, если вектор направления прямой:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

Наклон этой линии равен:

$m=\cfrac{\text{v}_2}{\text{v}_1}$

наклон под заданным углом

Наконец, если прямая образует угол

$\alpha$

в положительной части оси абсцисс (ось X) ее наклон эквивалентен тангенсу угла:

$m = \text{tg}(\alpha)$

Значение наклона линии

Имея всю информацию выше, мы уже прекрасно знаем, как найти наклон линии. Но на самом деле… что означает наклон линии?

Наклон линии указывает на вертикальные единицы, на которые линия поднимается для каждой горизонтальной единицы графика.

Например, в представлении следующей линии вы можете видеть, что она продвигается на 2 вертикальных единицы за каждую горизонтальную единицу, поскольку ее наклон равен 2.

Кроме того, наклон линии также указывает на ее крутизну:

Если линия увеличивается (поднимается), ее наклон положителен.
Если линия убывает (нисходящая), ее наклон отрицательный.
Если линия полностью горизонтальна, ее наклон равен 0.
Если линия полностью вертикальна, ее наклон равен бесконечности.

наклон положительной или отрицательной линии

Относительное положение линий

С другой стороны, относительное положение между двумя линиями можно узнать и по свойствам откосов:

Если две линии имеют разные наклоны, это означает, что они пересекаются , то есть пересекаются в точке.

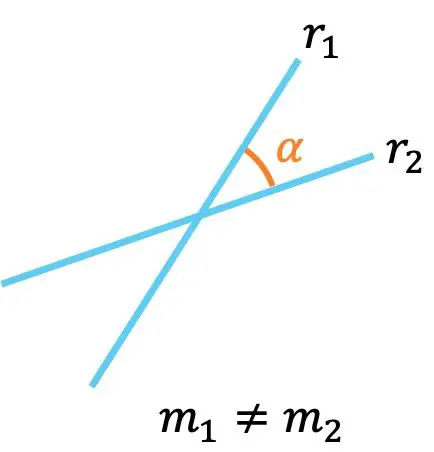
Кроме того, угол между двумя линиями поперек их наклонов можно рассчитать по следующей формуле:

$\text{tg}(\alpha) = \cfrac{m_2-m_1}{1+m_1\cdot m_2}$

Во-вторых, если две линии имеют одинаковый наклон, это означает, что они параллельны .

Наконец, наклоны двух перпендикулярных или ортогональных линий (образующих 90°) удовлетворяют следующему условию:

перпендикулярные линии, противоположные наклонам

Это один из способов узнать, параллельны или перпендикулярны две линии друг другу, однако существуют и другие методы, некоторые из которых даже быстрее. Чтобы узнать больше, вы можете перейти к объяснению перпендикулярности и параллельности между линиями . Кроме того, на этих страницах также объясняется, как найти линию, перпендикулярную (или параллельную) другой.

Решенные проблемы наклона линии

Упражнение 1

Найдите наклон линии, проходящей через следующие две точки:

$P_1(5,6) \qquad P_2(8,3)$

посмотреть решение

Для расчета наклона линии необходимо воспользоваться формулой:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{3-6}{8-5}=\cfrac{-3}{3} = \bm{-1}$

Упражнение 2

Рассчитайте наклон линии, проходящей через следующие две точки:

$P_1(-3,1) \qquad P_2(-2,-4)$

посмотреть решение

Чтобы найти наклон линии, необходимо воспользоваться формулой:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-4-1}{-2-(-3)}=\cfrac{-5}{-2+3}=\cfrac{-5}{1} = \bm{-5}$

Упражнение 3

Каков наклон каждой линии?

$\begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}$

посмотреть решение

А) Линия выражается в виде неявного уравнения, поэтому ее наклон равен 2 (член, сопровождающий

$x$

Б) Линия определяется уравнением наклона точки, поэтому ее наклон равен 4 (число перед круглыми скобками).

В) Линия имеет форму неявного уравнения, поэтому ее наклон равен:

$m= - \cfrac{A}{B} = -\cfrac{6}{2} = \bm{-3}$

Г) Линия задается в виде параметрических уравнений, поэтому сначала нужно найти ее вектор направления и с его помощью можно рассчитать наклон линии. Таким образом, компонентами вектора направления являются члены, сопровождающие коэффициент

$t:$

$\vv{\text{v}} = (-1,2)$

И как только мы узнаем вектор направления линии, мы сможем определить наклон линии:

$m = \cfrac{\text{v}_2}{\text{v}_1} = \cfrac{2}{-1} = \bm{-2}$

Упражнение 4

Определите наклон каждой изображенной на графике линии:

явное уравнение прямой, решение упражнения шаг за шагом

посмотреть решение

синий правый

Синяя линия увеличивается на один Y для каждого X, поэтому ее наклон равен 1.

$m=1$

прямо зеленый

Зеленая линия увеличивается на три Y для каждого X, поэтому ее наклон равен 3 .

$m=3$

Красная линия

Красная линия уменьшается на два Y для каждого X, поэтому ее наклон равен -2 .

$m=-2$

Формула наклона линии

Пример расчета наклона линии из двух точек

Нахождение наклона прямой по ее уравнению

Наклон по явному уравнению линии

Наклон с учетом уравнения наклона точки линии.

Наклон с учетом неявного уравнения линии

Наклон с учетом вектора направления линии

наклон под заданным углом

Значение наклона линии

Относительное положение линий

Решенные проблемы наклона линии

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Оставьте комментарий Отменить ответ