Наклонная асимптота

В этой статье мы объясним, что такое наклонные асимптоты функции. Вы узнаете, когда функция имеет наклонную асимптоту и как она вычисляется. А, кроме того, вы сможете увидеть примеры наклонных асимптот и потренироваться на пошагово решаемых упражнениях.

Что такое наклонная асимптота?

Наклонная асимптота функции — это наклонная линия, к которой ее график приближается бесконечно, ни разу не пересекая ее. Следовательно, все наклонные асимптоты представляют собой линии с уравнением y=mx+n .

Наклон и начало наклонной асимптоты рассчитываются по следующим формулам:

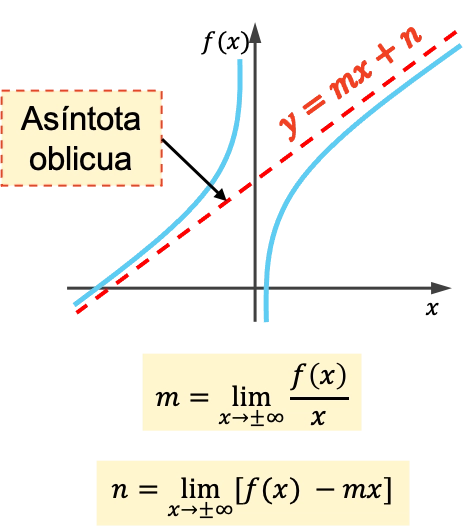
Как вычислить наклонную асимптоту функции

Для вычисления наклонной асимптоты функции необходимо выполнить следующие действия:

1. Вычислите предел бесконечности функции, разделенной на x.
2. Если приведенный выше предел дает ненулевое действительное число, это означает, что функция имеет наклонную асимптоту. Более того, наклон указанной наклонной асимптоты будет значением, полученным на пределе.



3. В этом случае остается только вычислить точку пересечения наклонной асимптоты, решив следующий предел:

Примечание: пределы необходимо рассчитывать на плюс и минус бесконечность, но обычно они дают один и тот же результат, поэтому мы упрощаем, полагая ±∞. Но если бы пределы плюс и минус бесконечность были разными, левую наклонную асимптоту и правую наклонную асимптоту пришлось бы рассчитывать отдельно.

Пример наклонной асимптоты

Далее мы возьмем наклонную асимптоту следующей рациональной функции, чтобы вы могли увидеть пример того, как это делается:

Наклонные асимптоты имеют вид

Итак, сначала мы вычисляем наклон линии

с соответствующей формулой:

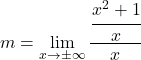
Чтобы устранить этот предел, мы должны применить свойства дробей:

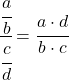
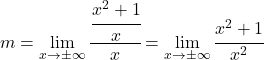
А теперь посчитаем лимит:

В этом случае результатом неопределенности бесконечности между бесконечностями является деление коэффициентов при х высшей степени, так как числитель и знаменатель имеют один и тот же порядок.

Приведенный выше предел дает ненулевое действительное число, поэтому функция имеет наклонную асимптоту. Теперь мы рассчитаем y-пересечение

асимптоты, используя соответствующую формулу:

Пробуем вычислить лимит:

Но мы получаем неопределенность бесконечность минус бесконечность. Поэтому необходимо привести слагаемые к общему знаменателю. Для этого умножим и разделим х на знаменатель дроби:

Теперь, когда эти два термина имеют одинаковый знаменатель, мы можем сгруппировать их:

Оперируем числителем:

И, наконец, мы разрешаем предел:

Итак, n = 0. Следовательно, наклонная асимптота является линейной функцией:

Изучаемая функция представлена на графике ниже. Как видите, функция подходит очень близко к линии y=x, но никогда не касается ее, поскольку это наклонная асимптота:

Решенные упражнения на косые асимптоты

Упражнение 1

Найдите наклонную асимптоту следующей рациональной функции:

Наклонные асимптоты имеют вид

, поэтому необходимо вычислить параметры m и n . Сначала мы вычисляем m , применяя его формулу:

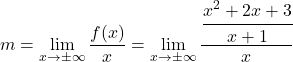
Упростим дробь, применив свойства дробей:

И решаем предел:

Итак, м = 1. Давайте теперь вычислим точку пересечения наклонной асимптоты, применив ее формулу:

Пробуем вычислить лимит:

Но мы получаем неопределенную форму бесконечность минус бесконечность. Поэтому мы должны привести эти термины к общему знаменателю, а затем сгруппировать их:

И, наконец, мы разрешаем предел:

Короче говоря, наклонная асимптота функции:

Упражнение 2

Найдите все наклонные асимптоты следующей рациональной функции:

Сначала воспользуемся формулой наклона наклонной асимптоты:

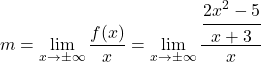
Упростим дробь, применив свойства дробей:

И определяем лимит:

Предел дает действительное число, отличное от нуля, поэтому это рациональная функция с наклонной асимптотой, наклон которой равен 2.

Теперь давайте вычислим перехват, применив соответствующую формулу:

Пробуем вычислить лимит:

Но мы получаем разностную неопределенность бесконечностей. Поэтому приводим слагаемые к общему знаменателю и далее действуем:

И, наконец, мы разрешаем предел:

Таким образом, наклонная асимптота дробной функции: