Компланарные линии

На этой странице вы узнаете, что означает, когда две прямые лежат в одной плоскости. Вы также сможете увидеть, когда две прямые лежат в одной плоскости, и, кроме того, вы найдете примеры и решенные упражнения с копланарными линиями.

Что такое две копланарные прямые?

В аналитической геометрии определение компланарных линий следующее:

Две прямые называются копланарными, если они лежат в одной плоскости. Следовательно, копланарные линии могут быть только секущими , параллельными или совпадающими линиями .

Более того, двух копланарных линий достаточно, чтобы полностью определить плоскость. Хотя очевидно, что плоскость может иметь более двух компланарных прямых, на самом деле каждая плоскость содержит бесконечное количество прямых.

С другой стороны, если две прямые не компланарны, это означает, что они пересекаются.

Примеры копланарных линий

Чтобы вы лучше поняли концепцию копланарных линий, вот пример с тремя линиями:

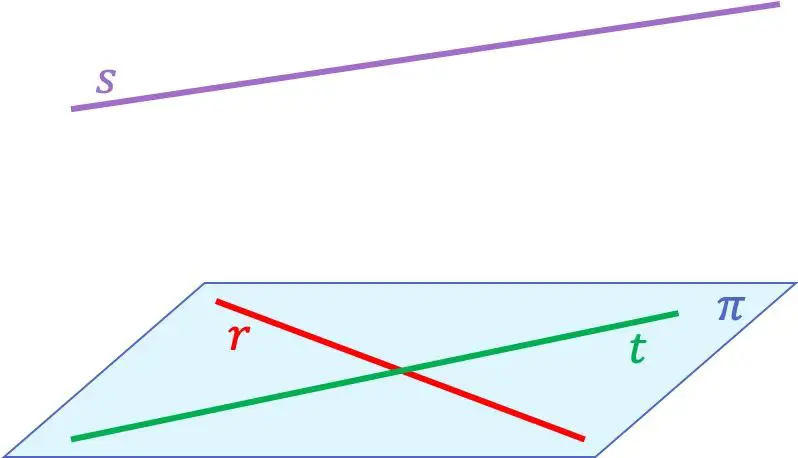
В этом случае строки

И

Они компланарны, потому что принадлежат одной плоскости. Вместо этого прямая линия

не компланарна ни с одной из двух других прямых, так как пересекает прямые

И

Как узнать, что две прямые лежат в одной плоскости?

Как мы видели выше при объяснении копланарных прямых, это могут быть только секущие, параллельные или совпадающие прямые. Другими словами, две пересекающиеся прямые никогда не будут компланарными.

Следовательно, чтобы узнать, являются ли две прямые компланарными, необходимо определить относительное положение между ними, и если это две пересекающиеся, параллельные или совпадающие прямые, это означает, что они являются компланарными прямыми.

Таким образом, чтобы проверить компланарность двух линий, нужно сначала знать, как вычислить взаимное положение двух линий в пространстве . Если вы еще не знакомы с этой концепцией, лучше всего сначала просмотреть ссылку, где вы найдете полное объяснение, а также примеры, упражнения и решенные задачи.

Решенное упражнение по копланарным линиям

В качестве примера решим типичное упражнение на копланарные прямые:

• Определите, являются ли следующие две прямые компланарными:

Первое, что нам нужно сделать, это найти относительное положение между двумя линиями, и для этого мы должны выразить обе линии одним и тем же типом уравнения. Тогда мы пересечем прямую линию

от общего (или неявного) уравнения к параметрическим уравнениям:

Таким образом, вектор направления каждой линии равен:

Координаты векторов направления двух линий пропорциональны, поэтому они могут быть только совпадающими или параллельными линиями. Следовательно, в данном конкретном случае нет необходимости вычислять точное взаимное положение, поскольку параллельные прямые и совпадающие прямые являются компланарными линиями. Таким образом, эти две линии компланарны .