На этой странице вы узнаете, что такое копланарные векторы и как определить, являются ли 2, 3, 4 или более векторов компланарными. Кроме того, вы сможете увидеть примеры и упражнения, решаемые шаг за шагом для копланарных векторов.
Что такое копланарные векторы?
В аналитической геометрии смысл компланарных (или копланарных) векторов следующий:
Компланарные векторы — это векторы, принадлежащие одной плоскости.
Следовательно, два вектора всегда компланарны, поскольку плоскость можно составить всего из двух векторов. С другой стороны, при наличии 3, 4 и более векторов возможно, что один из векторов не содержится в одной плоскости и, следовательно, они не компланарны.
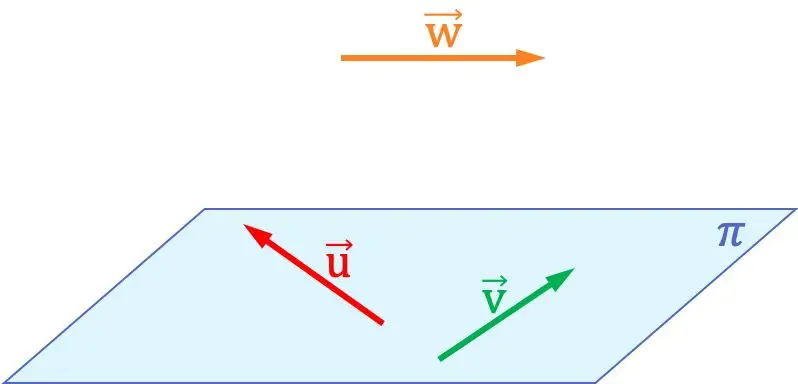
Например, на графике выше вы можете видеть, что векторы
![]()
И
![]()
они компланарны друг другу, так как содержатся в одной плоскости. С другой стороны, эти два вектора не компланарны вектору
![]()
, потому что в пространстве, содержащем три вектора, не может быть сформирована плоскость.
Из этого свойства мы можем сделать вывод, что если 3 или более вектора компланарны, точки, которые определяют указанные векторы (начало и конец вектора), также являются компланарными точками.
Когда векторы являются компланарными?
Как мы видели в определении копланарных (или копланарных) векторов, два вектора всегда компланарны, но более двух векторов не обязаны соблюдать соотношение компланарности.
Таким образом, существует несколько методов определения того, являются ли три и более вектора компланарными:
- Если смешанное произведение трех векторов (или тройное скалярное произведение) равно нулю, это означает, что три вектора компланарны. Если вам не очень понятно, как рассчитывается эта операция, я рекомендую вам посмотреть, что такое смешанное произведение трех векторов , здесь вы найдете объяснение, а также примеры и решенные упражнения.
![]()
- Если набор векторов может быть выражен как линейная комбинация двух векторов, это означает, что они компланарны, а это означает, что 3 или более векторов компланарны тогда и только тогда, когда они линейно зависимы. Чтобы показать, что три и более вектора представляют собой линейную комбинацию двух векторов, достаточно, чтобы ранг матрицы, образованной всеми векторами, был равен 2.
![]()
Важно, чтобы вы хорошо понимали концепцию линейной зависимости и независимости , то есть, когда два вектора линейно зависимы или линейно независимы, и что это означает. Если вам не совсем понятно, по ссылке вы найдете очень подробное объяснение, где, кроме того, можно увидеть примеры и пошагово решенные упражнения.
- Если рассматриваемые векторы являются параллельными векторами , это означает, что они также компланарны, то есть все параллельные векторы содержатся в одной плоскости.
![]()
Решенные задачи компланарных векторов
Упражнение 1
Определите, являются ли следующие три вектора компланарными:
![]()
![]()
![]()
Чтобы проверить, являются ли это 3 копланарными векторами, мы должны вычислить смешанное произведение между тремя векторами:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a1e4b0655c0a3f0165c880f5e64cce0_l3.png)
Смешанное произведение трех векторов равно нулю, поэтому эти три вектора компланарны .
Упражнение 2
Определите, являются ли следующие три вектора компланарными:
![]()
![]()
![]()
Один из способов проверить, имеем ли мы дело с тремя компланарными векторами, — это найти смешанное произведение между тремя векторами. Однако если мы внимательно посмотрим на компоненты векторов, то увидим, что они пропорциональны. Следовательно, три вектора параллельны друг другу.
![]()
А поскольку все векторы параллельны, они фактически являются тремя компланарными векторами .
Упражнение 3
Определите, являются ли следующие четыре вектора компланарными:
![]()
![]()
![]()
![]()
Чтобы узнать, являются ли четыре вектора компланарными, мы должны вычислить ранг матрицы, состоящей из всех векторов:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8384924c86edafd568505d5f80e1705d_l3.png)
В этом случае мы вычисляем объем указанной матрицы по определителям:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2778435c7f53952adf072419af8b268c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-82f278494a221879cc86da92ab4378c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-889142ac348173dd6c838633007f2d06_l3.png)
![]()
Ранг матрицы, образованной всеми векторами, эквивалентен 2, поэтому 4 вектора компланарны .
Упражнение 4
Рассчитать значение параметра
![]()
так что следующие 4 точки лежат в одной плоскости:
![]()
![]()
![]()
![]()
Чтобы четыре точки были компланарными, определяемые ими векторы должны быть компланарными. Поэтому мы вычисляем эти векторы:
![]()
![]()
![]()
Чья векторная матрица:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png)
Чтобы результирующие векторы были компланарными, ранг матрицы должен быть равен 2. И, следовательно, определитель всей матрицы 3х3 должен быть равен 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png)
![]()
Наконец, мы решаем неизвестное
![]()
![]()
![]()