Вы, наверное, слышали о комплексных числах . Это, пожалуй, самый трудный набор чисел, поскольку они сочетают в себе действительные и мнимые числа. Его унификация позволяет изучать числовое поведение, которое невозможно рассматривать, используя только действительные числа.
Что такое комплексные числа?
Комплексные числа представляют собой комбинацию действительного и мнимого чисел . Например, 4 + 5i — комплексное число, имеющее действительную часть, равную 4, и мнимую часть, равную 5i. В общем виде их можно выразить следующей формулой:
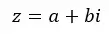
Где Re(z) = a и Im(z) = b
Как мы хорошо говорили, комплексы — это самое большое множество или глобальное множество , в которое входят как действительные числа, так и мнимые числа. Далее мы покажем вам небольшую схему иерархической структуры всех наборов:

Следовательно, когда у нас есть комбинация действительного и мнимого чисел, мы имеем комплексное число. Но бывают случаи, когда одна из двух частей равна нулю. Что происходит в этих случаях? Что ж, мы по-прежнему имеем дело с комплексами, потому что комплексный набор включает в себя все остальные числовые наборы. Но мы входим в другую подкатегорию:
| комплексное число | королевская вечеринка | часть воображения | Подкатегория |
| 2+5и | 2 | 5и | Сложный |
| 4 | 4 | 0 | чистый королевский |
| 3я | 0 | 3я | Чистое воображение |
Когда у нас есть чистое действительное число, поскольку мнимое значение b равно нулю, оставшееся комплексное число эквивалентно:
z = а + 0i = а
С другой стороны, когда у нас есть чистое воображение, а равно нулю и, следовательно, комплексное число остается следующим:
г = 0 + би = би
Графическое представление комплексных чисел
Для представления комплексных чисел мы используем комплексную плоскость . Состоит из двух линий : реальной и воображаемой. Эти две числовые линии используются для графического расположения чисел в каждом наборе, и если мы сложим их вместе, мы получим план, например:

Ось X называется реальной осью, потому что именно там расположены значения реальных деталей. Хотя ось Y называется мнимой осью, именно здесь записываются мнимые значения. Давайте посмотрим на примере, поместим число 3+2i в комплексную плоскость.

Как вы видели на изображении, мы определили число, используя цифры 3 и 2 в качестве координат, каждая для оси. Если вы хотите узнать больше о представлении комплексных чисел, рекомендуем прочитать эту статью.
Каковы типы комплексных чисел?
Теперь мы увидим, как можно выразить комплексное число. До сих пор мы видели только базовую форму (называемую биномиальной формой), которая записывается в виде суммы: действительная часть плюс мнимая часть.
Но на самом деле у нас есть три формы: биномиальная, полярная и тригонометрическая . Каждый тип выражения имеет свои свойства и используется в той или иной ситуации. Итак, мы собираемся объяснить их все и показать, как переходить от одного к другому.
1. Биномиальная форма
Комплексные числа в биномиальной форме записываются как сумма действительной и мнимой частей: a + bi. Например, число 6 + i представляет собой комплекс, выраженный в биномиальной записи. В этом случае формула всегда одна и та же:

Следовательно, чтобы выразить комплексное число в биномиальной форме, вам нужно знать только его действительное значение и мнимое значение.
Например, значение 3 + 2i имеет биномиальную форму и, как мы видели ранее, представляется следующим образом:

Биномиальная форма в основном используется для решения сложения и вычитания комплексных чисел.
2. Полярная форма
Чтобы выразить комплексные числа в полярной форме , необходимо вычислить их модуль |z| и его аргумент. Полярная форма в основном используется, когда нам нужно решить умножение и деление комплексных чисел.
Чтобы вычислить модуль комплексного числа, просто вычислите модуль a и b, как объяснено в следующей формуле:

И чтобы вычислить аргумент или угол z, нам нужно вычислить арктангенс b между a:

Важно отметить, что для точного определения значения угла α необходимо определить, в каком квадранте он находится. Действительно, функция арктангенса вычисляет только углы между π/2 и -π/2. Чтобы определить, в каком квадранте находится комплексное число, мы должны посмотреть значения a и b (положительные или отрицательные они):
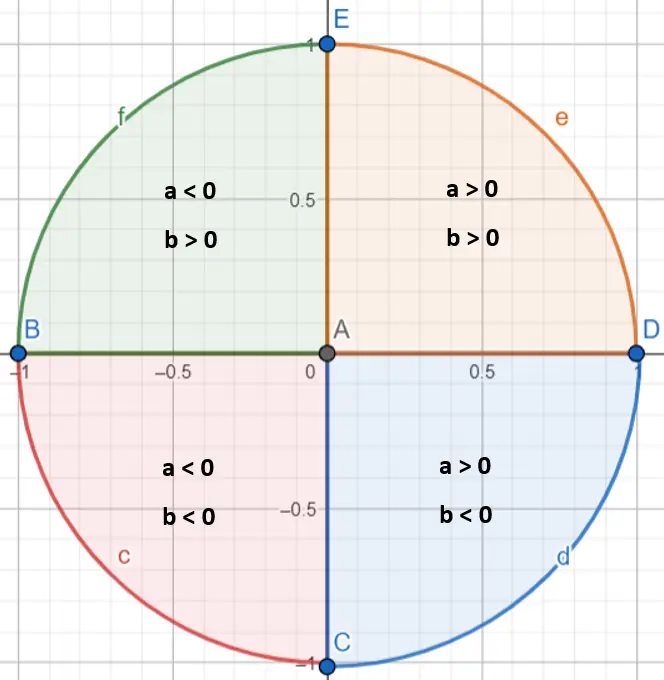
Как только мы узнаем, в какой квадрант попадает наше число, нам нужно следовать нескольким правилам:
- Если комплексное число находится в первом квадранте (a > 0 и b > 0), оставим аргумент как есть.
- Если комплексное число находится во втором квадранте (a < 0 и b > 0), мы добавим к аргументу π.
- Если комплексное число находится в третьем квадранте (a < 0 и b < 0), мы вычитаем π из аргумента.
- Если комплексное число находится в четвертом квадранте (a > 0 и b < 0), мы добавим к аргументу 2π.
Если вы не понимаете, о чем мы говорим, когда говорим «квадрант», советуем вам обратиться к нашей статье о тригонометрических соотношениях .
Зная величину и аргумент z, мы можем выразить комплексное число в полярной форме. Хотя эта форма принимает несколько номенклатур, две основные из них:

Например, если мы хотим изменить число 3 + 5i на полярное, нам просто нужно выполнить следующую процедуру.
Сначала вычисляем модуль:
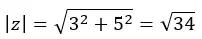
Затем мы вычисляем аргумент, который находится в первом квадранте, поэтому он остается таким, каким мы его вычислили.
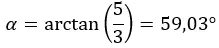
И выразим число в полярной форме:
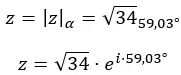
Его графическое представление выглядит следующим образом:
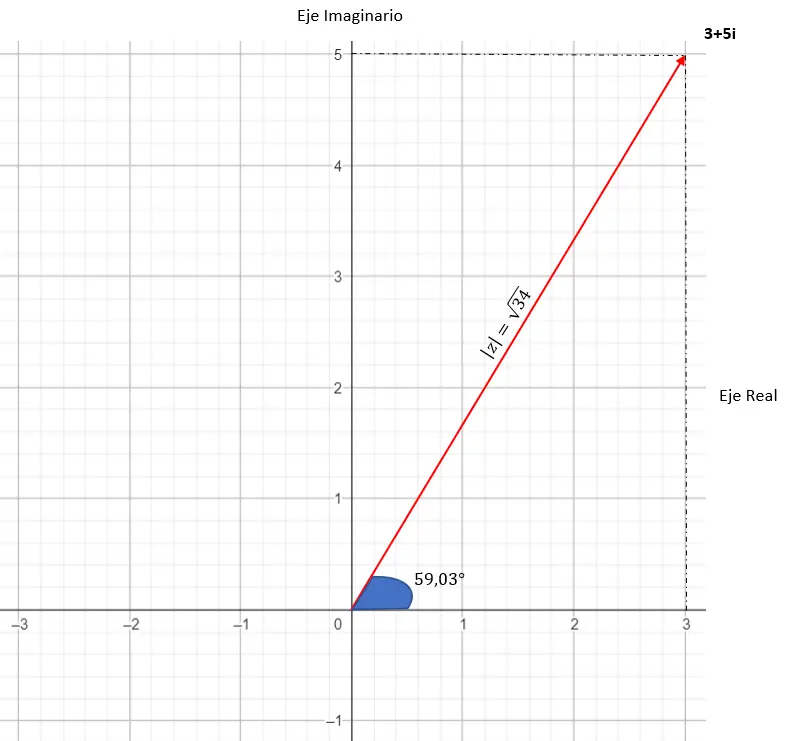
3. Тригонометрическая форма.
Наконец, у нас есть тригонометрическая запись , которая рассчитывается по формуле Эйлера :

Например, чтобы выразить число 4 – 3i в тригонометрической форме, мы следуем следующей процедуре:
Начнем с расчета модуля и аргумента по формулам, которые мы использовали в разделе полярной формы.
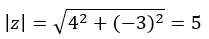
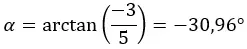
ВНИМАНИЕ: Аргумент находится в четвёртом квадранте, поскольку (a > 0 и b < 0).
Добавляем данные в уравнение в тригонометрической форме.
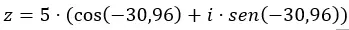
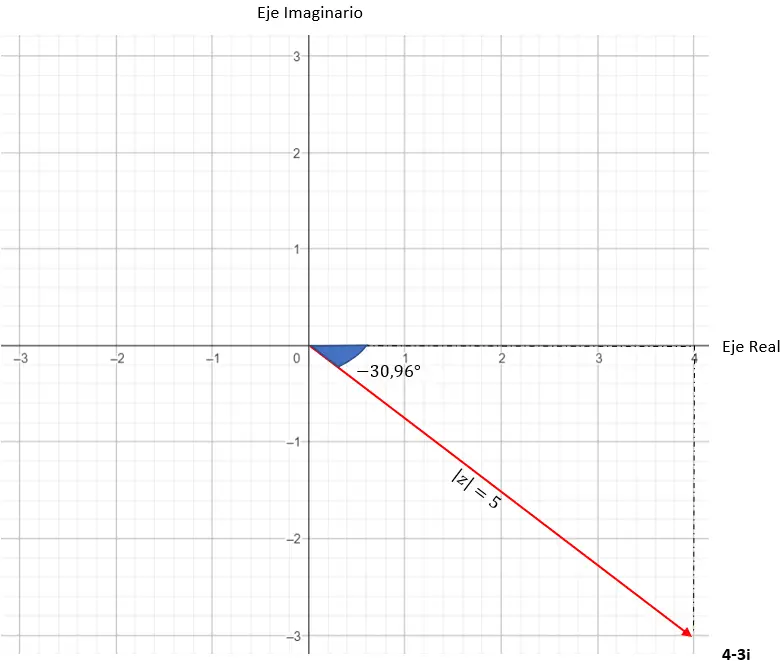
И у нас уже есть число, выраженное в тригонометрической форме. Его графическое представление выглядит следующим образом.
Как перейти с одного типа на другой?
Теперь вы знаете все способы выражения комплексного числа. В последнем разделе вы смогли увидеть, как получить доступ к каждой из них, но прежде чем мы закончим, мы хотим дать краткое описание того, как переходить от одной формы к другой. Только вам придется использовать формулы , которые мы видели в предыдущем разделе.
От биномиальной формы к полярной и наоборот
Чтобы перейти от биномиального к полярному, мы предлагаем следующую диаграмму:
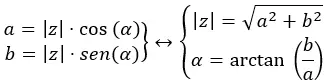
Ранее мы видели пример, когда мы перешли от биномиального к полярному, поэтому теперь мы перейдем от полярного к биномиальному, используя диаграмму выше. Нам нужно преобразовать √41 38,66 в бином.
Сначала вычислим а.
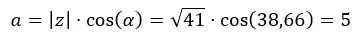
Затем вычисляем б.
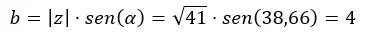
И мы выражаем это в биномиальной форме.
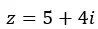
Графическое представление этого числа выглядит следующим образом:
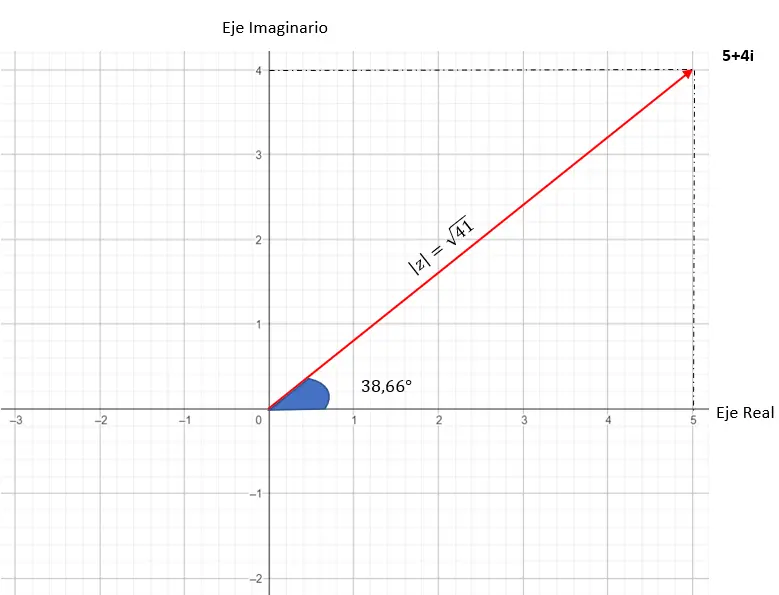
От биномиальной формы к тригонометрической форме и наоборот.
Чтобы перейти от биномиального к тригонометрическому, вам также необходимо применить формулы, о которых мы говорили в предыдущем разделе. Таким способом мы сначала вычисляем модуль и аргумент, затем подставляем эти данные в уравнение тригонометрического вида. В качестве примера мы передадим число z = 3 + 2i тригонометрически.
Сначала мы вычисляем модуль и аргумент.
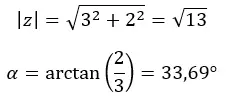
ВНИМАНИЕ: Аргумент находится в первом квадранте, поскольку (a > 0 и b > 0).
Затем этими данными дополняем уравнение тригонометрической формы.
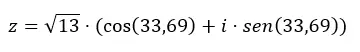
И если мы хотим перейти от тригонометрического к биномиальному, все, что нам нужно сделать, это решить предыдущее выражение.
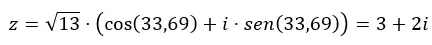
От полярной формы к тригонометрической форме и наоборот.
Наконец, мы перейдем от полярной формы к тригонометрической форме. Это довольно просто, поскольку эти две формы выражаются одними и теми же двумя значениями: по модулю и аргументу . Так что вам просто нужно заполнить формы и все.
Приведем пример, преобразуем число z = √85 12,53 в тригонометрическую форму.
Переформулируем две переменные (модуль и аргумент) в уравнение тригонометрической формы:
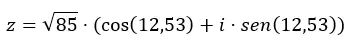
Итак, теперь, когда вы знаете, как переходить из одной формы в другую, мы рекомендуем немного потренироваться с помощью нескольких упражнений . Таким образом вы закрепите знания, полученные в этой статье. Если у вас есть вопросы по этой теме, смело задавайте их в комментариях. А если вы хотите узнать больше о комплексных числах, перейдите по ссылкам ниже.
Дополнительная информация о комплексных числах
- мнимые числа
- Свойства комплексных чисел
- Операции с комплексными числами
- корни комплексных чисел
- Графическое представление комплексных чисел