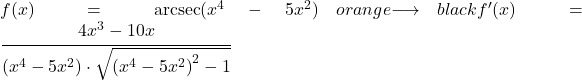На этой странице вы увидите, чему равна производная арксеканса (формула). Вы найдете решенные упражнения для производных арксеканса функции.
Формула производной арсеканса
Производная арксеканса x равна произведению x на корень из x в квадрате минус 1.
![]()
Следовательно, производная арксеканса функции равна частному производной этой функции, деленному на функцию, умноженную на корень этой функции, возведенный в квадрат минус один.
![]()
Очевидно, что вторая формула аналогична первой, единственное различие между ними состоит в том, что во второй формуле применяется цепное правило.

Хотя это может показаться странным, поскольку это обратные функции, производная арксеканса не имеет ничего общего с производной секанса. Формулу производной секущей можно увидеть, нажав здесь:
➤ См.: производная секущей.
Примеры производной арксеканса
Пример 1
На этом примере мы увидим, чему равна производная арксеканса линейной функции 7x.
![]()
Чтобы найти производную арксеканса, необходимо применить соответствующую ей формулу, которая выглядит следующим образом:
![]()
Производная функции 7x равна 7, поэтому производная арксеканса функции 7x равна:
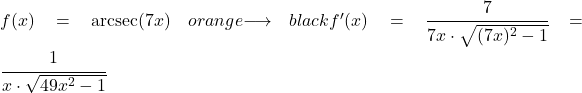
Пример 2
Во втором примере мы выведем арксеканс потенциальной функции.
![]()
Поскольку в аргументе функции арксеканса есть член, отличный от x, нам нужно применить правило производной арксеканса с правилом цепочки, чтобы получить всю функцию.
![]()
Итак, в числителе пишем производную от аргумента функции, а в знаменателе переписываем потенциальную функцию и умножаем ее на квадратный корень из функции аргумента, возведенной в степень 2 минус 1: