La régression linéaire est une méthode statistique utilisée pour étudier la relation entre deux variables continues . L’idée principale de la régression linéaire est de trouver la ligne droite qui correspond le mieux aux données. De plus, il permet de prédire la valeur d’une variable en fonction de la valeur d’une autre.
Cette ligne droite est appelée “régression” et est utilisée pour prédire des valeurs inconnues ou pour comprendre la relation entre les variables. En résumé, la régression linéaire est un outil pour analyser et modéliser la relation entre deux variables continues.
Pourquoi la régression linéaire est-elle importante ?
La régression linéaire est importante car elle permet de modéliser et d’analyser la relation entre deux variables continues , ce qui peut être utile pour prédire les valeurs futures et identifier les modèles et les tendances dans les données.
De plus, la régression linéaire est un outil fondamental en statistique et dans la plupart des domaines de la recherche scientifique et sociale, y compris l’économie, la psychologie, la médecine, l’ingénierie et la physique, entre autres. Il est également utilisé dans la prise de décision commerciale et l’optimisation des processus dans l’industrie et les entreprises.
En résumé, la régression linéaire est un outil puissant et polyvalent qui permet l’analyse et une meilleure compréhension des données et des relations entre les variables dans divers domaines de recherche et de pratique.
Quels sont les types de régression linéaire ?
Il existe plusieurs types de régression linéaire, dont certains sont :
régression linéaire simple
L’analyse de régression linéaire simple est un outil largement utilisé pour étudier l’effet d’une variable indépendante sur une seule variable dépendante , dans laquelle on considère qu’il existe une relation linéaire entre elles. L’équation de régression linéaire simple permet d’estimer les valeurs de la variable dépendante en fonction des valeurs de la variable indépendante.
La formule de régression linéaire simple est :
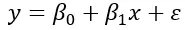
Où, β 0 est la valeur de la variable dépendante lorsque la variable indépendante est égale à zéro. β 1 représente la variation de la variable dépendante par unité de variation de la variable indépendante et ε représente le résidu ou l’erreur. C’est-à-dire la variabilité des données qui ne peut être expliquée par la relation linéaire de la formule.
La régression linéaire multiple
La régression linéaire multiple est utilisée lorsqu’il y a plus d’une variable indépendante qui peut affecter la variable dépendante étudiée.
La formule de régression linéaire multiple est :
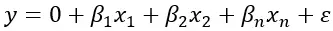
Où Y représente la variable dépendante, β 1 , β 2 , β n sont les variables indépendantes qui peuvent affecter la valeur de Y, X 1 , X 2 , X n sont les valeurs des variables indépendantes, 0 est l’intersection de la droite de régression et ε représente l’éventuelle erreur existante. Cette formule nous permet d’estimer la valeur de Y en fonction des valeurs des variables indépendantes.
Quelle est la formule de régression linéaire ?
La formule de régression linéaire est :
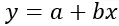
Où:
y est la variable dépendante (ou réponse) à prédire
x est la variable indépendante (ou prédictive) utilisée pour faire la prédiction
a est l’ordonnée à l’origine (ou le point où la ligne de régression coupe l’axe Y lorsque x=0)
b est la pente de la droite de régression (indiquant le taux de changement de y pour chaque changement de x)
Pour trouver les valeurs de a et b, on utilise la méthode des moindres carrés qui cherche à minimiser la somme des erreurs quadratiques entre les valeurs observées et les valeurs prédites par la droite de régression.
Voici les formules :
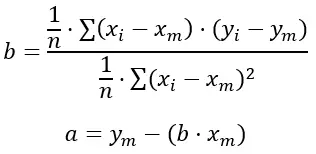
Où:
n est le nombre total d’ensembles de données dont nous disposons.
x i et y i sont les valeurs que nous prenons dans la sommation.
x m et y m sont les valeurs moyennes de chaque variable.
Comment appliquer la méthode de régression linéaire ?
La méthode de régression linéaire peut être appliquée en suivant les étapes ci-dessous :
- Collecter des données : La première chose à faire est de collecter les données qui vous intéressent. Par exemple, si vous souhaitez étudier la relation entre le salaire et l’âge d’un groupe de personnes, vous devez collecter des informations sur le salaire et l’âge de chacune d’entre elles.
- Tracer les données – Ensuite, vous devez tracer les données sur un plan cartésien, où la variable indépendante (dans ce cas, l’âge) est placée sur l’axe horizontal et la variable dépendante (salaire) est placée sur l’axe vertical.
- Déterminer la droite de régression : La droite de régression qui correspond le mieux aux données doit être déterminée. Cette ligne est obtenue à partir de la formule de régression linéaire, qui est calculée à l’aide des données statistiques de l’échantillon .
- Évaluer la qualité de l’ajustement – Il est important d’évaluer la qualité de l’ajustement de la ligne de régression aux données. Cela peut être fait en utilisant des mesures statistiques.
- Faire des prédictions – Enfin, des prédictions peuvent être faites à l’aide de la droite de régression obtenue. Par exemple, si vous souhaitez prédire le salaire d’une personne de 30 ans, vous devez utiliser la formule de régression linéaire et y substituer la valeur de l’âge.
Il est important de noter que ces étapes peuvent varier légèrement selon le type de régression linéaire utilisé et le logiciel statistique utilisé.
A quoi sert la régression linéaire ?
La régression linéaire est utilisée lorsque vous souhaitez analyser la relation entre deux variables , où une variable peut affecter la valeur d’une autre variable. Par conséquent, la régression linéaire peut être utilisée pour comprendre comment une variable indépendante affecte une variable dépendante et pour prédire la valeur de la variable dépendante en fonction de la variable indépendante.
Il est important de noter que la régression linéaire suppose que la relation entre les deux variables est linéaire , ce qui signifie que le changement de la variable dépendante est proportionnel au changement de la variable indépendante.
Par conséquent, la régression linéaire doit être utilisée lorsqu’une relation linéaire entre les deux variables est suspectée. Si cette condition n’est pas remplie, il peut être plus approprié d’utiliser d’autres modèles de régression non linéaire ou différentes méthodes statistiques.
Quelles sont les applications de la régression linéaire ?
La régression linéaire est utilisée dans une grande variété d’applications dans des domaines tels que les statistiques, l’économie, l’ingénierie, les sciences sociales, la biologie, entre autres. Voici quelques-unes des applications les plus courantes de la régression linéaire :
- Analyse des tendances – Pour analyser les tendances des données historiques et prévoir les tendances futures.
- Prévision – Prédire la valeur future d’une variable en fonction des valeurs passées d’une ou plusieurs variables.
- Etude de marché : étude de la relation entre la demande d’un produit et son prix.
- Analyse financière – Étudier la relation entre les revenus et les dépenses d’une entreprise et prévoir les résultats financiers futurs.
- Etudes épidémiologiques : étudier la relation entre l’exposition à un facteur de risque et la probabilité de développer une maladie.
- Sciences sociales – Étudier la relation entre deux ou plusieurs variables dans des domaines tels que la psychologie, la sociologie et les sciences politiques.
- Recherche opérationnelle – La régression linéaire est utilisée pour modéliser et optimiser des systèmes complexes dans des domaines tels que l’ingénierie industrielle et la logistique.
- Sciences de l’environnement – Utilisé pour étudier la relation entre les facteurs environnementaux et les effets sur les écosystèmes.
Que sont les résidus dans la régression linéaire ?
Les résidus en régression linéaire sont la différence entre les valeurs observées de la variable dépendante et les valeurs prédites par le modèle de régression linéaire . En d’autres termes, il s’agit de la distance verticale entre les points de données réels et la droite de régression.
L’idée derrière les résidus est que si la ligne de régression correspond bien aux données, les résidus doivent être petits et aléatoires. Si les résidus sont importants ou suivent un certain schéma, cela peut être un signe que la relation entre les variables n’est pas linéaire ou que le modèle de régression linéaire n’est pas adapté aux données.
Les résidus sont également utilisés pour évaluer la précision du modèle de régression linéaire et pour identifier les valeurs aberrantes ou les points de données influents susceptibles d’affecter la qualité du modèle.
Puis-je exécuter une régression linéaire avec plus d’une variable dépendante ?
Dans la régression linéaire, la variable dépendante est toujours une variable unique. Cependant, vous pouvez avoir plus d’une variable indépendante. Dans ce cas, on parlerait de régression linéaire multiple .
Dans la régression linéaire multiple, le but est d’étudier l’effet de plusieurs variables indépendantes sur une seule variable dépendante.
Comment puis-je interpréter les coefficients en régression linéaire?
Dans la régression linéaire, les coefficients représentent la pente et l’ordonnée à l’origine de la droite de régression . La pente indique la variation de la variable dépendante par unité de variation de la variable indépendante, tandis que l’ordonnée à l’origine représente la valeur de la variable dépendante lorsque la variable indépendante est égale à zéro.
Exemples numériques de régression linéaire
Un exemple simple peut être le suivant :
Supposons que nous disposions des données d’âge et de taille suivantes pour un groupe de personnes :
| Années d’âge) | Hauteur (cm) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| Quatre cinq | 190 |
Nous voulons déterminer s’il existe une relation entre l’âge et la taille de ces personnes. Pour ce faire, nous utiliserons la régression linéaire.
Tout d’abord, nous pouvons dessiner un graphique statistique avec les données (dans ce cas, nous vous recommandons d’utiliser un nuage de points) :
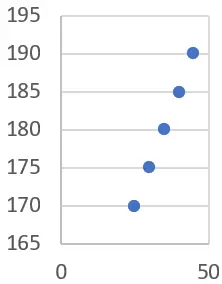
Nous pouvons voir qu’il existe une tendance claire selon laquelle à mesure que l’âge augmente, la taille augmente également. Nous pouvons le confirmer en calculant la droite de régression linéaire.
En calculant les coefficients de la droite de régression linéaire avec les formules que nous avons vues précédemment, nous obtenons :
à = 145
b = 1
Par conséquent, l’équation de la droite de régression linéaire est :
Taille = 145 + 1 Âge
Nous pouvons utiliser cette équation pour prédire la taille d’une personne en fonction de son âge. Par exemple, si une personne a 32 ans, nous pouvons prédire que sa taille serait :
Hauteur = 145 + 1 32 = 177 cm