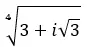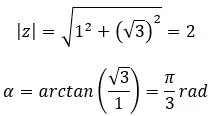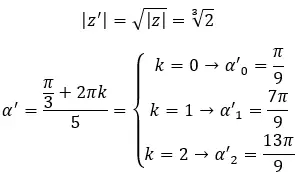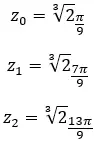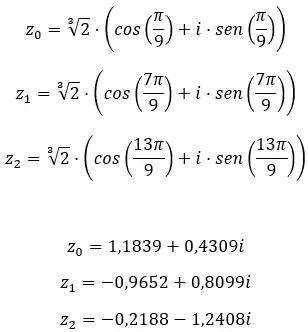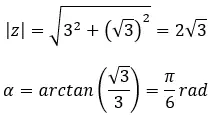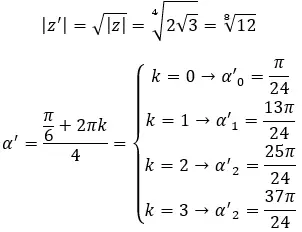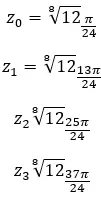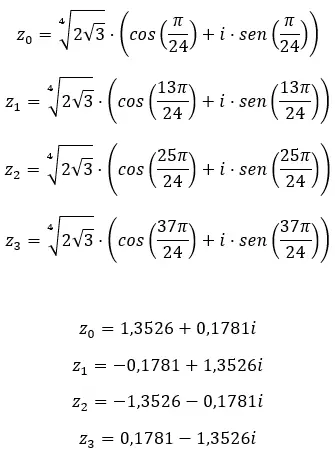Le calcul des racines des nombres complexes est assez simple. Bon, une fois qu’on a compris la procédure, c’est assez répétitif. Ensuite, nous allons l’expliquer et nous vous donnerons un exemple, afin que vous puissiez apprendre à l’appliquer dans de vrais exercices.
racines nièmes de nombres complexes
Le concept de racine nième équivaut à dire racine d’ordre n, par conséquent, la même méthode est utilisée pour calculer la racine carrée et la racine cinquième d’un nombre complexe. Bien sûr, le nombre de solutions changera en fonction de cet ordre.
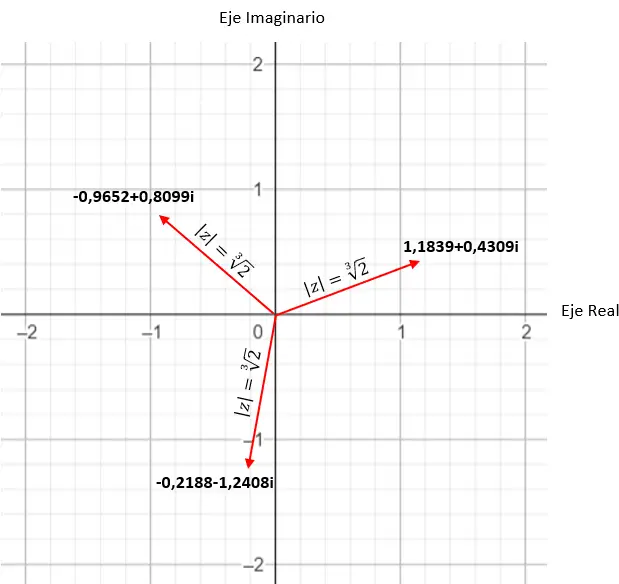
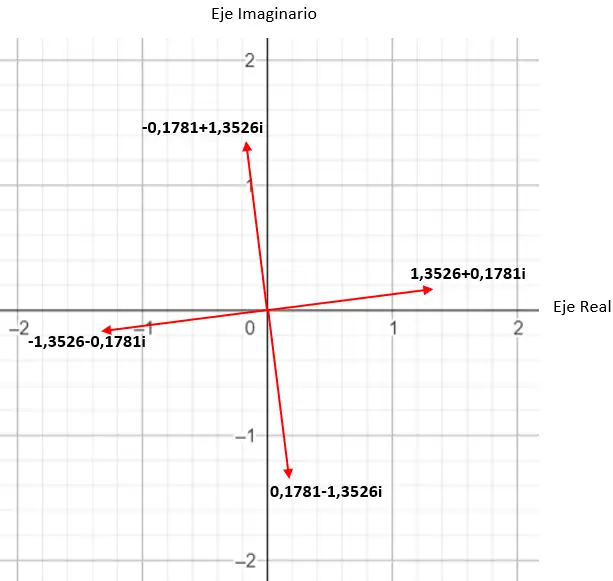
Par exemple, si on calcule la quatrième racine d’un complexe, on obtient 4 solutions différentes. Et si on l’exprime dans le plan complexe , on voit qu’un polygone régulier à 4 côtés se forme, centré sur l’origine du plan. C’est une propriété très intéressante, que nous verrons en détail plus tard (dans la section des exemples).
Maintenant que nous avons clarifié ce concept, nous allons voir comment calculer la racine d’un nombre complexe sous forme polaire (utiliser cette notation est la plus confortable pour résoudre une racine.). Simplement, vous devez calculer la racine du module et exprimer l’argument en fonction de n. En d’autres termes, la racine du nombre complexe suivant (z) :
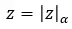
Cela revient à calculer :
- Module : La nième racine du module initial.
- Argument : Ajoutez 2πk en radians ou 360k en degrés à l’argument, et divisez par n.
Mathématiquement, pour calculer le module et l’argument on utilise les deux formules suivantes :
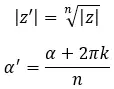
Où, k = 0, 1, 2, …, n-1.
Et, par conséquent, nous exprimons le résultat comme suit :
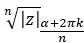
Pour être clair, les n solutions que nous obtiendrons en résolvant cette racine seront formées par le même module et n arguments différents.
Exemples de calcul de racines nièmes de complexes
Nous allons maintenant voir quelques exemples sur le calcul des racines nièmes de nombres complexes. Nous vous recommandons d’essayer de les résoudre par vous-même et lorsque vous avez terminé, regardez le correctif. N’oubliez pas que la méthode est expliquée juste au dessus.
Trouvez la troisième racine du nombre complexe : 1 + i √3 .
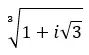
Trouvez la quatrième racine du nombre complexe : 3+i √ 3 .