Sur cette page, vous trouverez l’explication de ce que sont les composants (ou coordonnées) d’un vecteur. Aussi, vous pourrez voir comment ils sont calculés à partir de deux points et même comment ils se décomposent à travers leur module et leur angle. De plus, vous trouverez des exemples et des exercices résolus étape par étape.
Quelles sont les composantes d’un vecteur ?
Les composantes d’un vecteur sont les projections d’un vecteur sur les axes cartésiens. Par conséquent, la projection du vecteur sur l’axe des abscisses est la composante X du vecteur et, de la même manière, la projection du vecteur sur l’axe des ordonnées est la composante Y du vecteur.
Les composants d’un vecteur peuvent également être appelés les coordonnées d’un vecteur.
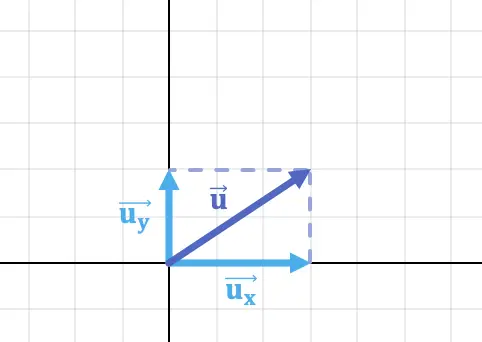
Par exemple, la composante horizontale et la composante verticale du vecteur dans l’image ci-dessus sont :
![]()
![]()
Donc le vecteur est :
![]()
Par conséquent, les composants d’un vecteur peuvent également être définis comme la représentation d’un vecteur dans un système de coordonnées. Évidemment, s’il s’agit d’un système à deux dimensions (en r2) le vecteur aura deux composantes, en revanche, s’il s’agit d’une base à trois dimensions (en r3) le vecteur sera composé de trois composantes.
Les composantes cartésiennes d’un vecteur sont si importantes car avec elles nous pouvons connaître les caractéristiques du vecteur, qui sont principalement la direction, le sens et le module (ou grandeur) du vecteur. De plus, ils sont utilisés pour effectuer des opérations vectorielles.
Comment calculer les composantes d’un vecteur à partir de deux points
Nous venons de voir comment trouver graphiquement les coordonnées d’un vecteur, cependant, on peut aussi déterminer numériquement ses composantes.
Pour calculer numériquement les composantes d’un vecteur, nous avons besoin de connaître deux points : son origine et sa fin, ou en d’autres termes, où il commence et où il se termine. Puisque les composantes d’un vecteur sont les coordonnées que l’on obtient en soustrayant son extrémité moins son origine.
![]()
Par exemple, nous allons calculer le vecteur dont l’origine est le point A(3,1) et sa fin est le point B(5,4) :
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c740536015a29149532a4a1eb46f4f7_l3.png)
Comme vous pouvez le voir, déterminer les composantes d’un vecteur n’est pas très difficile, cependant, c’est assez important. Par exemple, l’un des types de vecteurs les plus couramment utilisés sont les vecteurs perpendiculaires (ou orthogonaux) ; Eh bien, si vous comprenez quelles sont les coordonnées d’un vecteur, il est très facile de calculer des vecteurs perpendiculaires. Vous pouvez voir comment c’est fait dans l’explication des vecteurs orthogonaux .
Comment calculer les composantes d’un vecteur à partir de son module et de son angle
Vous pouvez également trouver les composants d’un vecteur à partir de sa magnitude et de l’angle qu’il fait avec l’axe X. Ce processus est appelé décomposition vectorielle .
Ainsi, les composantes X et Y du vecteur peuvent être calculées avec les rapports trigonométriques du cosinus et du sinus :

Comme vous pouvez le voir sur l’image, le module d’un vecteur et ses composants complètent un triangle rectangle, de sorte que les formules élémentaires de la trigonométrie peuvent être appliquées.
Si vous ne vous souvenez pas comment le module d’un vecteur est calculé, vous pouvez consulter ce qu’est le module d’un vecteur . Vous trouverez ici la formule de la magnitude d’un vecteur, ainsi que des exemples, des exercices résolus étape par étape et toutes les propriétés de la magnitude d’un vecteur. C’est une explication très complète donc vous la comprendrez parfaitement. ✅
Contrairement à la magnitude d’un vecteur qui est toujours positive, ses composantes peuvent être négatives car le sinus et le cosinus peuvent prendre des valeurs négatives.
A titre d’exemple, nous allons faire la décomposition vectorielle du vecteur dont le module et l’angle avec l’axe OX sont :
![]()
La composante X du vecteur est égale au module multiplié par le cosinus de l’angle :
![]()
Et la composante Y du vecteur est égale au produit du module par le sinus de l’angle :
![]()
Donc les coordonnées du vecteur sont :
![]()