Vetores perpendiculares ou ortogonais

Nesta página você encontrará tudo sobre vetores perpendiculares (ou ortogonais): o que são, quando dois vetores são ortogonais, como encontrar um vetor perpendicular a outro, as propriedades dos vetores perpendiculares,… Além disso, você poderá ver vários exemplos e exercícios resolvidos para vetores perpendiculares ou ortogonais.

O que são dois vetores perpendiculares ou ortogonais?

Em matemática, dois vetores são ortogonais (ou perpendiculares ) quando formam um ângulo reto (90º) entre si.

No gráfico a seguir, você pode ver dois vetores perpendiculares:

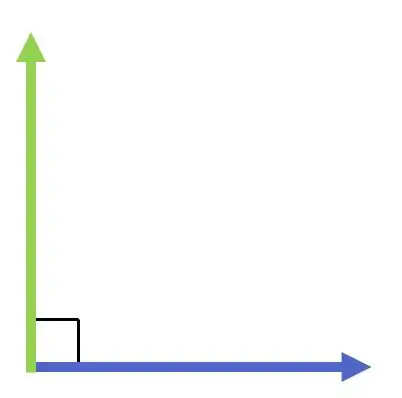
quando dois vetores são ditos perpendiculares ou ortogonais

Por outro lado, a perpendicularidade de dois vetores depende apenas da sua direção, e não do seu módulo (ou magnitude) ou, obviamente, da sua direção. Ou seja, dois vetores serão perpendiculares se fizerem um ângulo de 90 graus, tenham ou não o mesmo comprimento.

Como saber se dois vetores são ortogonais ou perpendiculares?

Como acabamos de ver, graficamente é muito fácil ver se dois vetores são perpendiculares. No entanto, você também pode determinar se dois vetores são ortogonais sem representá-los graficamente:

Numericamente, dois vetores são ortogonais ou perpendiculares quando seu produto escalar é zero (0).

Por exemplo, mostraremos que os dois vetores a seguir são perpendiculares sem representá-los graficamente:

$\vv{\text{u}}=(3,2) \qquad\vv{\text{v}}=(-2,3)$

Para verificar se estes são vetores perpendiculares (ou ortogonais), aplicamos a fórmula do produto escalar :

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(3,2)\cdot (-2,3) \\[1.5ex]&=3\cdot (-2) + 2 \cdot 3 \\[1.5ex] & = -6+6 \\[1.5ex] & =\bm{0} \end{aligned}$

O resultado do produto escalar dos dois vetores é zero, então esses são dois vetores ortogonais (ou perpendiculares) entre si.

$\vv{\text{u}}\bm{\perp} \vv{\text{v}}$

Observe que dois vetores são indicados como perpendiculares pelo símbolo

$\bm{\perp}}.$

Portanto, o produto escalar entre dois vetores perpendiculares é zero. Porém, o produto vetorial de dois vetores (outro tipo de multiplicação entre vetores) dá o oposto: um vetor perpendicular aos outros dois. Portanto, é importante saber distinguir os dois tipos de operações, você pode perceber as diferenças entre elas nas propriedades do produto vetorial .

Como é calculado um vetor perpendicular ou ortogonal a outro?

A forma mais simples de calcular um vetor perpendicular a outro no plano (em R2) é intercalar as duas coordenadas do vetor e também mudar o sinal para um.

E para obter um vetor perpendicular a outro no espaço (em R3) é necessário interpor duas coordenadas entre si, depois mudar o sinal de uma delas e, por fim, colocar a coordenada em zero restante.

Para que você possa ver as diferenças no cálculo de um vetor ortogonal para outro dependendo se eles possuem 2 ou 3 coordenadas, resolveremos um exercício com cada tipo de vetor.

Encontre um vetor perpendicular ou ortogonal no plano cartesiano

Determine um vetor perpendicular ao seguinte vetor bidimensional:

$\vv{\text{v}}=(4,1)$

Por se tratar de um vetor com apenas duas componentes, para obter um vetor perpendicular é necessário alternar suas componentes e negar uma delas:

$\vv{\mathbf{u}}\bm{=(-1,4)}$

Podemos verificar pela fórmula do produto escalar que estes são de fato vetores perpendiculares:

$\vv{\text{v}} \cdot \vv{\text{u}}=(4,1)\cdot (-1,4) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Determine um vetor perpendicular ou ortogonal no espaço cartesiano

Calcule um vetor ortogonal ao seguinte vetor tridimensional:

$\vv{\text{v}}=(2,3,-1)$

Neste caso, temos um vetor de três componentes, portanto, para obter um vetor perpendicular, precisamos alternar duas de suas componentes, alterar o sinal de uma delas e converter a coordenada restante em zero:

$\vv{\mathbf{u}}\bm{=(3,-2,0)}$

Podemos verificar com a fórmula do produto escalar que estes são de fato vetores ortogonais:

$\vv{\text{v}} \cdot \vv{\text{u}}=(2,3,-1)\cdot (3,-2,0) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Propriedades de vetores perpendiculares e ortogonais

Os vetores perpendiculares têm as seguintes características:

Relação simétrica : se um vetor é perpendicular a outro vetor, então esse vetor também é perpendicular ao primeiro vetor.

$\vv{\text{u}} \bm{\perp} \vv{\text{v}} \ \longrightarrow \ \vv{\text{v}} \bm{\perp} \vv{\text{u}}$

Propriedade irreflexiva : Obviamente, nenhum vetor pode ser perpendicular a si mesmo.

$\vv{\text{v}} \ \cancel{\bm{\perp}}} \ \vv{\text{v}}$

Na geometria euclidiana (em R2), qualquer par de vetores perpendiculares a um terceiro vetor deve ser necessariamente paralelo. Ou seja, se um vetor é perpendicular a outro vetor e esse vetor também é perpendicular a um terceiro vetor, o primeiro e o último vetores são paralelos. Isto se deve ao quinto postulado de Euclides .

Por outro lado, você também deve saber que graças a essas propriedades a regra do saca-rolhas pode ser utilizada. Essa técnica facilita o cálculo de um tipo de operação vetorial que, sem essa regra, demoraria muito para ser resolvida. Você pode ver o que é isso clicando na explicação da regra do saca-rolhas .

Conceitos relacionados a vetores perpendiculares ou ortogonais

Existem dois tipos de vetores muito próximos dos vetores perpendiculares: vetores normais e vetores orthomarle. Embora todos estejam relacionados entre si, queremos esclarecer como eles diferem para evitar qualquer possível confusão.

Um vetor normal é um vetor perpendicular a um plano. Assim, também pode ser incluído no conceito de ortogonalidade de um vetor, mas neste caso é perpendicular a um plano em vez de outro vetor.

Por outro lado, dois vetores ortonormais são dois vetores mutuamente ortogonais que, além disso, são vetores unitários (de magnitude igual a 1).

Por fim, deve-se destacar também que é muito comum a utilização de bases ortogonais (bases vetoriais formadas a partir de vetores perpendiculares entre si) e até bases ortonormais . Na verdade, o referencial cartesiano é uma base ortonormal.