Vetores paralelos - Mathority

Nesta página você encontrará tudo sobre vetores paralelos: o que significam, quando dois vetores são paralelos, como encontrar um vetor paralelo a outro vetor, as propriedades deste tipo de vetor,… Além disso, você poderá ver vários exemplos e exercícios de vetores paralelos resolvidos.

O que são vetores paralelos?

Vetores paralelos são vetores que possuem a mesma direção. Em outras palavras, dois vetores são paralelos se estiverem contidos em duas retas paralelas. Portanto, dois vetores paralelos formam um ângulo entre eles de 0 ou 180 graus.

Por exemplo, os três vetores a seguir são paralelos:

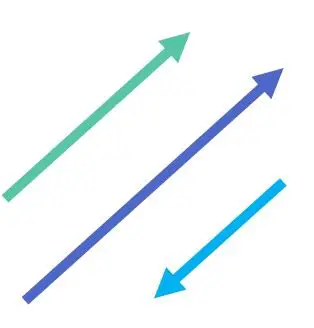
Além disso, o paralelismo de dois vetores depende apenas da sua direção. Ou seja, dois vetores serão paralelos se coincidirem em direção, quer tenham a mesma direção ou direção oposta. E o mesmo acontece com o módulo (ou magnitude), dois vetores podem ter módulos diferentes e ser paralelos.

Por outro lado, quando dois vetores têm a mesma direção, mas opostas, eles são chamados de vetores antiparalelos .

Como você sabe se dois vetores são paralelos?

Dois vetores são paralelos quando são proporcionais. Portanto, para saber se dois vetores são paralelos, precisamos determinar se as suas respectivas componentes são proporcionais ou não.

Veremos como saber se dois vetores são paralelos através de dois exercícios resolvidos diferentes, um com vetores com 2 coordenadas e outro com vetores com 3 coordenadas.

Exemplo de vetores paralelos ao plano (em R2)

Determine se os dois vetores a seguir são paralelos:

$\vv{\text{u}}=(-2,4) \qquad\vv{\text{v}}=(1,-2)$

Para saber se são realmente vetores paralelos, devemos verificar se suas coordenadas cartesianas são proporcionais:

$\cfrac{-2}{1} = \cfrac{4}{-2} = -2$

Dividir as componentes X e as componentes Y entre elas dá o mesmo resultado (-2), portanto os dois vetores são proporcionais e portanto também paralelos .

$\vv{\text{u}} \parallel \vv{\text{v}}$

Observe que em matemática, quando dois elementos geométricos são paralelos, isso é indicado por duas barras verticais (II).

Exemplo de vetores paralelos no espaço (em R3)

Descubra se a condição de paralelismo é satisfeita nos dois vetores a seguir:

$\vv{\text{u}}=(1,3,-2) \qquad\vv{\text{v}}=(2,6,4)$

Para determinar se são de fato vetores paralelos, devemos verificar se as coordenadas dos vetores são proporcionais:

$\cfrac{1}{2} = \cfrac{3}{6} = 0,5 \neq \cfrac{-2}{4} = -0,5$

As componentes X e as componentes Y dos vetores são proporcionais entre si porque ao dividi-las obtemos o mesmo resultado, por outro lado, não são proporcionais à componente Z. Portanto, os vetores não são proporcionais a todos e, portanto, não são paralelos .

$\vv{\text{u}} \ \cancel{\parallel} \ \vv{\text{v}}$

Como calcular um vetor paralelo?

Para encontrar um vetor paralelo a outro vetor, basta multiplicá-lo por um escalar (um número real) diferente de zero (0). Há, portanto, um número infinito de vetores paralelos entre si, pois o vetor pode ser multiplicado por um número infinito de números.

Por exemplo, calcularemos vários vetores paralelos do seguinte vetor:

$\vv{\text{v}}=(2,4)$

O resultado de todos os produtos a seguir são vetores paralelos ao vetor anterior:

$2\vv{\text{v}}=(4,8)$

$3\vv{\text{v}}=(6,12)$

$-1\vv{\text{v}}=(-2,-4)$

$\displaystyle \frac{1}{2}\vv{\text{v}}=(1,2)$

Propriedades de vetores paralelos

Vetores paralelos têm as seguintes características:

Propriedade reflexiva : cada vetor é paralelo a si mesmo.

$\vv{\text{v}} \parallel \vv{\text{v}}$

Propriedade simétrica : se um vetor é paralelo a outro, esse vetor também é paralelo ao primeiro. Esta propriedade também é possuída por vetores perpendiculares .

$\vv{\text{u}} \parallel \vv{\text{v}} \ \longrightarrow \ \vv{\text{v}} \parallel \vv{\text{u}}$

Propriedade transitiva : se um vetor é paralelo a outro vetor, e este segundo vetor é paralelo a um terceiro vetor, o primeiro vetor também é paralelo ao terceiro vetor.

$\left. \begin{array}{c} \vv{\text{u}} \parallel \vv{\text{v}} \\[2ex] \vv{\text{v}} \parallel \vv{\text{w}} \end{array} \right\} \longrightarrow \ \vv{\text{u}} \parallel \vv{\text{w}}$

O produto escalar de dois vetores paralelos é igual ao produto de seus módulos. Você pode verificar por que isso está acontecendo em particular nas propriedades do produto escalar .

$\vv{\text{u}} \parallel \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}} \cdot \vv{\text{v}}= \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert$

Dois vetores paralelos são sempre linearmente dependentes. Este conceito é muito importante, portanto, se você não o conhece, pode consultar o que são dois vetores linearmente dependentes .

$\vv{\text{u}} \parallel \vv{\text{v}} \ \longrightarrow \ LD$