Todos os vetores linearmente independentes e dependentes

Nesta página explicamos o que são vetores linearmente independentes e linearmente dependentes. Você também verá exemplos de como saber se um conjunto de vetores é linearmente dependente ou independente. E, além disso, você encontrará exercícios e problemas resolvidos passo a passo sobre independência e dependência linear.

O que são vetores linearmente independentes?

Um conjunto de vetores livres é linearmente independente se nenhum deles puder ser escrito como uma combinação linear dos outros.

Em outras palavras, dado um conjunto de vetores

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Estes são linearmente independentes se a única solução para a seguinte equação:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

Esses são todos os coeficientes

$a_i$

igual a 0:

$a_1=a_2=\dots = a_n=0$

Geometricamente, dois vetores são linearmente independentes se não tiverem a mesma direção, ou seja, se não forem paralelos.

Para resumir, às vezes dizemos diretamente que são vetores LI. Ou que os vetores têm independência linear.

O que são vetores linearmente dependentes?

Obviamente, vetores linearmente dependentes significam o oposto de vetores linearmente independentes. Sua definição é portanto:

Um conjunto de vetores livres do plano é linearmente dependente se algum deles puder ser expresso como uma combinação linear de outros vetores que formam o sistema.

Em outras palavras, dado um conjunto de vetores

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Eles são linearmente dependentes se existir uma solução para a seguinte equação:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

em que tem certo coeficiente

$a_i$

é diferente de 0:

$a_i\neq 0$

O inverso também é verdadeiro: se um vetor é uma combinação linear de outros vetores, então todos os vetores do conjunto são linearmente dependentes.

Além disso, se dois vetores são paralelos, isso implica que são linearmente dependentes.

Às vezes eles também são abreviados e chamados simplesmente de vetores LD. Ou ainda que os vetores tenham dependência linear.

Exemplo de como saber se os vetores são linearmente dependentes ou independentes

Veremos então um exemplo típico de vetores linearmente dependentes e independentes.

Determine se os seguintes três vetores tridimensionais têm dependência ou independência linear:

$\vv{\text{u}} = (1,5,2)$

$\vv{\text{v}} = (-2,3,-1)$

$\vv{\text{w}} = (4,2,1)$

Primeiro, precisamos enunciar a condição de combinação linear:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

Agora substituímos cada vetor por suas coordenadas. Como zero, que corresponde ao vetor zero:

$a_1(1,5,2)+a_2(-2,3,-1)+ a_3(4,2,1)=(0,0,0)$

Os coeficientes multiplicam vetores, então a seguinte expressão é equivalente:

$(a_1,5a_1,2a_1)+(-2a_2,3a_2,-a_2) + (4a_3,2a_3,a_3)=(0,0,0)$

Adicionamos vetores:

$(a_1-2a_2+4a_3 \ , \ 5a_1+3a_2+2a_3 \ , \ 2a_1-a_2+a_3)=(0,0,0)$

Se olharmos atentamente, a expressão anterior corresponde a 3 equações, pois cada coordenada do vetor esquerdo deve ser igual a cada coordenada do vetor direito. Temos, portanto, um sistema homogêneo de 3 equações com 3 incógnitas:

$\left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}$

Portanto, a única coisa que precisamos fazer é resolver o sistema de equações cujas incógnitas são

$a_1, a_2$

$a_3.$

Para fazer isso, você pode usar qualquer método (método de substituição, método de Gaus, regra de Cramer, etc.). Porém, para saber se os vetores são LI ou LD basta determinar se existe uma solução diferente da solução trivial (todos os coeficientes iguais a zero). ENTÃO:

Se o determinante da matriz composta pelas componentes dos vetores for diferente de zero, isso significa que o sistema de equações possui apenas uma solução (
$a_1=a_2=a_3=\dots=0$

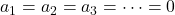
) e, portanto, os vetores são linearmente independentes
Por outro lado, se o determinante da matriz composta pelas componentes dos vetores for igual a zero, isso implica que o sistema de equações possui mais de uma solução e, portanto, os vetores são linearmente dependentes .

Então a única coisa que precisa ser calculada é o determinante com as coordenadas dos vetores (como é um determinante 3×3, pode ser resolvido com a regra de Sarrus). Este determinante corresponde aos coeficientes do sistema de equações anterior:

$\displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}$

Neste caso, o determinante é diferente de 0, portanto os vetores são linearmente independentes .

Portanto, a única solução possível para o sistema de equações é a solução trivial com todas as incógnitas iguais a zero:

$a_1=a_2=a_3=0$

Propriedades de vetores linearmente dependentes e independentes

A dependência linear ou independência de vetores possui as seguintes características:

Dois vetores proporcionais são paralelos e, portanto, linearmente dependentes porque têm a mesma direção.

Da mesma forma, se dois vetores não têm a mesma direção ou não são proporcionais, eles são linearmente independentes.

Três vetores coplanares (que estão no mesmo plano) são linearmente independentes.

O vetor nulo
$(\vv{\text{v}}=(0,0,0))$

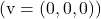
é linearmente dependente de qualquer vetor.

Um conjunto de vetores linearmente independentes gera um espaço vetorial e forma uma base vetorial. Se os três vetores forem perpendiculares, é uma base ortogonal. E se o seu módulo também for igual a 1, isso corresponde a uma base ortonormal.

Exercícios resolvidos de dependência linear e independência

Abaixo você encontra vários exercícios resolvidos sobre vetores linearmente dependentes e independentes para praticar.

Exercício 1

Determine se os seguintes vetores são linearmente dependentes ou independentes:

$\vv{\text{u}} = (1,-2,1)$

$\vv{\text{v}} = (2,1,3)$

$\vv{\text{w}} = (5,-1,1)$

Veja a solução

Primeiro colocamos a condição de combinação linear:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,-2,1)+a_2(2,1,3)+ a_3(5,-1,1)=(0,0,0)$

$(a_1,-2a_1,a_1)+(2a_2,a_2,3a_2) + (5a_3,-a_3,a_3)=(0,0,0)$

$(a_1+2a_2+5a_3 \ , \ -2a_1+a_2-a_3 \ , \ a_1+3a_2+a_3)=(0,0,0)$

A igualdade anterior corresponde ao seguinte sistema de equações lineares:

$\left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}$

Depois de declararmos o sistema de equações, resolvemos o determinante da matriz com seus termos:

$\displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}$

Neste caso, o determinante é diferente de 0, portanto os três vetores são linearmente independentes entre si.

Exercício 2

Classifique os seguintes vetores como linearmente dependentes ou independentes:

$\vv{\text{u}} = (1,4,3)$

$\vv{\text{v}} = (-2,0,2)$

$\vv{\text{w}} = (3,-1,-4)$

Veja a solução

Primeiramente colocamos a equação da combinação linear:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,4,3)+a_2(-2,0,2)+ a_3(3,-1,-4)=(0,0,0)$

$(a_1,4a_1,3a_1)+(-2a_2,0,2a_2) + (3a_3,-a_3,-4a_3)=(0,0,0)$

$(a_1-2a_2+3a_3 \ , \ 4a_1-a_3 \ , \ 3a_1+2a_2-4a_3)=(0,0,0)$

Da igualdade anterior obtemos o seguinte sistema homogêneo de equações:

$\left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}$

Depois de declararmos o sistema de equações, resolvemos o determinante da matriz com as coordenadas dos vetores:

$\displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}$

Neste caso, o determinante é equivalente a 0, portanto os três vetores dependem linearmente entre si.

Exercício 3

Para os três vetores a seguir, indique quais pares de vetores são linearmente dependentes e quais pares são linearmente independentes.

$\vv{\text{u}} = (1,2,-2) \qquad \vv{\text{v}} = (2,4,-3) \qquad \vv{\text{w}} = (-4,-8,6)$

Veja a solução

A maneira mais simples de saber se um par de vetores é linearmente dependente ou independente é verificar se eles são proporcionais.

Primeiro verificamos o vetor

$\vv{\text{u}}$

com o vetor

$\vv{\text{v}} :$

$\cfrac{1}{2} = \cfrac{2}{4} \neq \cfrac{-2}{-3} \ \longrightarrow \ \text{LI}$

Em segundo lugar, verificamos o vetor

$\vv{\text{u}}$

com o vetor

$\vv{\text{w}} :$

$\cfrac{1}{-4} = \cfrac{2}{-8} \neq \cfrac{-2}{6} \ \longrightarrow \ \text{LI}$

Finalmente, testamos o vetor

$\vv{\text{v}}$

com o vetor

$\vv{\text{w}} :$

$\cfrac{2}{-4} = \cfrac{4}{-8} = \cfrac{-3}{6} = -\cfrac{1}{2} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \text{LD}$

Assim, o único par de vetores que depende linearmente um do outro é

$\vv{\text{v}}$

$\vv{\text{w}}.$

Além disso, a relação deles é a seguinte:

$\vv{\text{v}}= -\cfrac{1}{2} \vv{\text{w}}$

Ou equivalente:

$\vv{\text{w}}= -2\vv{\text{v}}$

Por outro lado, os outros pares de vetores são linearmente independentes.

Exercício 4

Estude a dependência ou independência linear dos 4 vetores a seguir entre si:

$\vv{\text{u}} = (0,1,2)$

$\vv{\text{v}} = (-1,-2,0)$

$\vv{\text{w}} = (4,1,-1)$

$\vv{\text{x}} = (-2,-3,2)$

Veja a solução

Primeiro colocamos a condição de combinação linear:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}+a_4\vv{\text{x}}=0$

$a_1(0,1,2)+a_2(-1,-2,0)+ a_3(4,1,-1)+a_4(-2,-3,2)=(0,0,0)$

$(0,a_1,2a_1)+(-a_2,-2a_2,0) +(4a_3,a_3,-a_3)+(-2a_4,-3a_4,2a_4)=(0,0,0)$

$(-a_2+4a_3-2a_4\ , \ a_1-2a_2+a_3-3a_4 \ , \ 2a_1-a_3+2a_4)=(0,0,0)$

Neste caso temos um sistema de 3 equações com 4 incógnitas:

$\left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}$

Não podemos resolver o determinante de toda a matriz do sistema, pois apenas matrizes quadradas podem ser determinadas. Devemos portanto calcular todas as combinações possíveis de determinantes 3×3 e ver se um deles é igual a 0, caso em que os vetores serão linearmente dependentes, por outro lado, se todos os determinantes forem diferentes de 0 os 4 vetores serão ser linearmente independente.

Calculamos o determinante dos coeficientes

$a_1, a_2$

$a_3:$

$\displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}$

O determinante dos 3 primeiros coeficientes (ou dos 3 primeiros vetores) é diferente de zero. Então agora tentamos com o determinante dos coeficientes

$a_1, a_2$

$a_4:$

$\displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}$

Obtivemos um determinante zero, portanto não é necessário calcular os demais determinantes porque já sabemos que os 4 vetores são linearmente dependentes .