Vetores coplanares (ou coplanares)

Nesta página você aprenderá o que são vetores coplanares e como saber se 2, 3, 4 ou mais vetores são coplanares. Além disso, você poderá ver exemplos e exercícios resolvidos passo a passo de vetores coplanares.

O que são vetores coplanares?

Na geometria analítica, o significado dos vetores coplanares (ou coplanares) é o seguinte:

Vetores coplanares são vetores que pertencem ao mesmo plano.

Portanto, dois vetores são sempre coplanares porque um plano pode ser formado com apenas 2 vetores. Por outro lado, quando existem 3, 4 ou mais vetores, é possível que um dos vetores não esteja contido no mesmo plano e, portanto, não sejam coplanares.

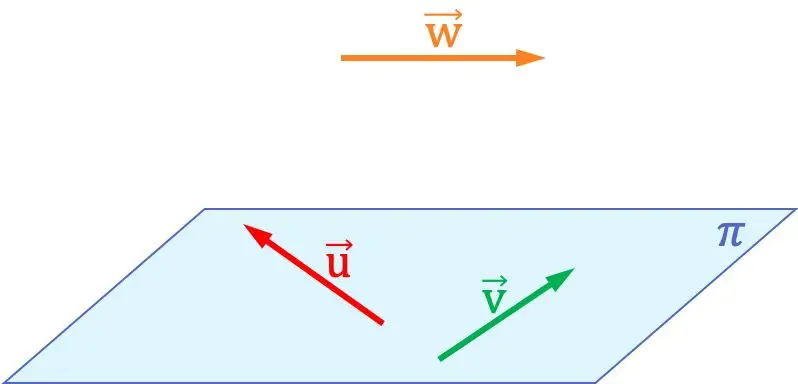
exemplos de vetores coplanares ou coplanares

Por exemplo, no gráfico acima você pode ver que os vetores

$\vv{\text{u}}$

$\vv{\text{v}}$

eles são coplanares entre si, pois estão contidos no mesmo plano. Por outro lado, estes dois vetores não são coplanares com o vetor

$\vv{\text{w}}$

, porque nenhum plano pode ser formado no espaço que contém os três vetores.

Desta propriedade podemos deduzir que se 3 ou mais vetores são coplanares, os pontos que definem esses vetores (início e fim do vetor) também são pontos coplanares.

Quando os vetores são coplanares?

Como vimos na definição de vetores coplanares (ou coplanares), dois vetores são sempre coplanares, mas mais de dois vetores não precisam respeitar a relação de coplanaridade.

Assim, existem vários métodos para determinar se três ou mais vetores são coplanares:

Se o produto misto de três vetores (ou produto escalar triplo) for igual a zero, significa que os três vetores são coplanares. Se você não tem muita clareza sobre como essa operação é calculada, recomendo que você dê uma olhada no que é o produto misto de três vetores , aqui você encontrará a explicação, além de exemplos e exercícios resolvidos.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] =0$

Se um conjunto de vetores pode ser expresso como uma combinação linear de dois vetores, isso implica que eles são coplanares, o que significa que 3 ou mais vetores são coplanares se e somente se forem linearmente dependentes. Para mostrar que três ou mais vetores são uma combinação linear de dois vetores, basta que o posto da matriz formada por todos os vetores seja igual a 2.

$rg(A) = 2$

É importante que você tenha um bom entendimento do conceito de dependência e independência linear , ou seja, quando dois vetores são linearmente dependentes ou linearmente independentes e o que isso significa. Se não estiver totalmente claro, no link você encontrará uma explicação bem detalhada, onde, além disso, poderá ver exemplos e exercícios resolvidos passo a passo.

Se os vetores em questão forem vetores paralelos , isso significa que também são coplanares, ou seja, todos os vetores paralelos estão contidos no mesmo plano.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Problemas resolvidos de vetores coplanares

Exercício 1

Determine se os três vetores a seguir são coplanares:

$\vv{\text{u}} = (3,1,2)$

$\vv{\text{v}} = (2,3,-1)$

$\vv{\text{w}} = (-1,-5,4)$

veja solução

Para verificar se se trata de 3 vetores coplanares, devemos calcular o produto misto entre os três vetores:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}$

O produto misto dos três vetores é zero, então os 3 vetores são coplanares .

Exercício 2

Determine se os três vetores a seguir são coplanares:

$\vv{\text{u}} = (4,-2,6)$

$\vv{\text{v}} = (-2,1,-3)$

$\vv{\text{w}} = (6,-3,9)$

veja solução

Uma forma de verificar se estamos lidando com 3 vetores coplanares seria resolver o produto misto entre os três vetores. Porém, se olharmos atentamente para as componentes dos vetores, podemos ver que elas são proporcionais. Portanto, os três vetores são paralelos entre si.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

E como todos os vetores são paralelos, eles são efetivamente 3 vetores coplanares .

Exercício 3

Determine se os quatro vetores a seguir são coplanares:

$\vv{\text{a}} = (2,1,1)$

$\vv{\text{b}} = (1,-1,2)$

$\vv{\text{c}} = (-1,0,-1)$

$\vv{\text{d}} = (3,1,2)$

veja solução

Para saber se os quatro vetores são coplanares, devemos calcular o posto da matriz composta por todos os vetores:

$\displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}$

Neste caso, calculamos o escopo da referida matriz por determinantes:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0$