▷ O que é um trinômio quadrado perfeito? (exemplos)

Nesta página explicamos o que é um trinômio quadrado perfeito e como ele é explicado. Além disso, você poderá ver vários exemplos e praticar passo a passo exercícios de trinômio quadrado perfeito.

O que é um trinômio quadrado perfeito?

Obviamente, antes de ver o significado de um trinômio quadrado perfeito, você precisa saber o que são trinômios , então recomendo dar uma olhada nesta página vinculada (onde é explicado em detalhes) antes de continuar.

Portanto, a definição de um trinômio quadrado perfeito é a seguinte:

Em matemática, um trinômio quadrado perfeito , também conhecido como TCP , é o trinômio obtido pela quadratura de um binômio.

Portanto, um trinômio quadrado perfeito consiste em um polinômio com dois quadrados perfeitos e outro termo que é o produto duplo das bases desses quadrados.

Como você pode ver nas duas fórmulas acima, o trinômio quadrado perfeito é obtido a partir de duas identidades notáveis (ou produtos notáveis), por isso é tão importante. Especificamente, um trinômio quadrado perfeito é encontrado ao resolver o quadrado de uma adição ou o quadrado de uma subtração .

Exemplos de trinômios quadrados perfeitos

Para finalizar a compreensão do conceito de trinômio quadrado perfeito, explicaremos 2 exemplos passo a passo:

Exemplo 1

$x^2+6x+9$

Este exemplo é um trinômio quadrado perfeito porque em sua expressão algébrica existem dois quadrados perfeitos (ou seja, eles têm uma raiz quadrada exata), pois

$x^2$

e 9 são equivalentes a

$x$

e 3 elevados respectivamente à potência de dois:

$(x)^2 = x^2$

$(3)^2 = 9$

E mais, o último termo restante do trinômio

$(6x)$

É obtido multiplicando as bases dos dois quadrados anteriores entre si e por 2:

$2\cdot x \cdot 3 = 6x$

Portanto, toda a identidade notável completa neste exercício seria:

$(x+3)^2 =x^2+6x+9$

Exemplo 2

$16x^2-40x+25$

Este outro exemplo também é um trinômio quadrado perfeito porque as 3 condições necessárias são atendidas: dois termos correspondem a dois quadrados perfeitos, e outro termo é o resultado da multiplicação das bases desses quadrados entre si e por 2.

$(4x)^2 = 16x^2$

$(5)^2 = 25$

$2\cdot 4x \cdot 5 =40x$

Neste caso o trinômio quadrado perfeito tem um monômio negativo, correspondendo portanto ao desenvolvimento da igualdade notável de uma diferença quadrada:

$(4x-5)^2 = 16x^2-40x+25$

Como fatorar um trinômio quadrado perfeito

Na álgebra, um problema muito comum é fatorar um trinômio quadrado perfeito (PCT). Caso você não saiba o que isso significa, fatorar um polinômio significa transformar sua expressão em um produto de fatores.

Assim, para fatorar este tipo de trinômio algébrico, devem ser respeitadas as seguintes regras:

O trinômio deve ter dois quadrados perfeitos, que chamaremos
$a^2$

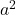
E

$b^2.$
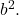
O terceiro termo restante do trinômio deve ser igual ao duplo produto das bases dos dois quadrados perfeitos, o que corresponde matematicamente à expressão
$2\cdot a \cdot b.$
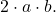
O trinômio fatorado será
$(a+b)^2$

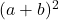
se todos os termos do trinômio quadrado perfeito forem positivos, caso contrário, se o produto duplo das bases dos quadrados tiver sinal negativo, o trinômio fatorado será

$(a-b)^2.$

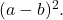
Para finalizar o entendimento do procedimento, resolveremos passo a passo um exercício:

Fatore o seguinte trinômio quadrado perfeito:

$x^2-12x+36$

A primeira coisa que precisamos fazer é identificar se o trinômio possui dois elementos que são quadrados perfeitos, ou seja, se sua raiz quadrada não dá um número decimal. Neste problema

$x^2$

é o quadrado da variável

$x$

e 36 é o quadrado de 6:

$\sqrt{x^2} = x$

$\sqrt{36} = 6$

O trinômio, portanto, tem dois quadrados perfeitos.

Em segundo lugar, devemos verificar se o termo intermédio é equivalente ao duplo produto das duas raízes calculado no passo anterior:

$2 \cdot x \cdot 6 = 12x$

Esta regra também é respeitada.

Então todas as condições são atendidas. Portanto, o trinômio quadrado perfeito fatorado é o binômio formado pelas duas raízes encontradas (

$x$

e o número 6) ao quadrado:

$x^2-12x+36=(x-6)^2$

Como o termo intermediário é negativo, devemos também colocar um sinal de menos entre parênteses. Por outro lado, se fosse positivo teríamos que somar uma soma:

$x^2+12x+36=(x+6)^2$

Logicamente, fatorar é um procedimento complicado então, além de tentar fazer o exercício abaixo, recomendo olhar estes exemplos de fatoração de polinômios . Neste link também explicamos um método que é usado não apenas para fatorar trinômios, mas também qualquer tipo de polinômio, e com a mesma rapidez.

Exercícios resolvidos do trinômio quadrado perfeito

Transforme os seguintes trinômios em binômios quadrados aplicando a fórmula correspondente:

$\text{A)} \ x^2+8x+16$

$\text{B)} \ x^2-14x+49$

$\text{C)} \ x^4-20x^2+100$

$\text{D)} \ 81x^2+90x+25$

$\text{E)} \ 64x^4-176x+121$

Veja a solução

Para converter um trinômio quadrado perfeito na potência de um binômio quadrado, você deve usar as fórmulas para as identidades notáveis do quadrado de uma soma e do quadrado de uma diferença, que são:

$(a+b)^2 = a^2+2ab+b^2$