▷ Como resolver todos os tipos de indeterminações (limites)

Neste artigo explicamos o que é indeterminação. Você descobrirá o que são todos os tipos de indeterminações e como resolvê-las. Além disso, você poderá ver exercícios resolvidos passo a passo sobre os limites de função de todas as indeterminações.

O que são indeterminações?

Indeterminações, também chamadas de formas indeterminadas, são expressões matemáticas que aparecem no cálculo dos limites de funções cujo resultado não está definido. Assim, para resolver as indeterminações dos limites, é necessário aplicar um procedimento preliminar que depende do tipo de função.

Ou seja, quando obtemos a indeterminação, não significa que o limite não exista ou que não possa ser resolvido, mas sim que teremos que fazer alterações na função para encontrar a solução do limite.

Tipos de indeterminações

As indeterminações, ou formas indeterminadas, são classificadas nos seguintes tipos:

Indeterminação infinito menos infinito (∞-∞)
Número de indeterminação entre zero (k/∞)
Indeterminação zero entre zero (0/0)
Indeterminação infinita entre o infinito (∞/∞)
Indeterminação 1 elevada ao infinito (1 ^∞ )
Indeterminação zero elevada a zero (0 ⁰ )
Indeterminação zero para o infinito (0·∞)
Indeterminação zero elevada ao infinito (0 ^∞ )
Indeterminação infinita levada a zero (∞ ⁰ )

Veremos então como resolver todos os tipos de indeterminações.

Infinito menos indeterminação infinita

A forma indeterminada infinito menos infinito não é igual a zero, pois subtraímos dois números muito grandes mas não sabemos qual é maior. O resultado da diferença dos infinitos depende, portanto, da ordem de cada infinito.

$\infty-\infty$

Resolver este tipo de indeterminação não é fácil, pois dependendo do tipo de função, um procedimento ou outro deve ser aplicado. Portanto, recomendamos que você visualize a explicação completa no seguinte link:

➤ Veja: como resolver a indeterminação infinito menos infinito

Número de indeterminação entre zero

A indeterminação de uma constante dividida por zero é obtida quando o denominador de uma função racional é cancelado.

$\cfrac{k}{0}$

O resultado deste tipo de forma indeterminada será sempre mais infinito, menos infinito ou o limite da função não existirá. Vejamos como essa indeterminação é calculada resolvendo um limite como exemplo:

$\displaystyle\lim_{x\to 0}\cfrac{-4}{x^2}=\cfrac{-4}{0^2}=\cfrac{-4}{0}=\infty$

Obtivemos a indeterminação de um número dividido por zero, então precisamos calcular os limites laterais da função:

$\displaystyle\lim_{x\to 0^-}\cfrac{-4}{0^2}=\cfrac{-4}{(-0,001)^2}=\cfrac{-4}{+0}=-\infty$

$\displaystyle\lim_{x\to 0^+}\cfrac{-4}{0^2}=\cfrac{-4}{0,001^2}=\cfrac{-4}{+0}=-\infty$

➤ Veja: o que são limites laterais?

Os dois limites laterais da função dão o mesmo resultado, então por definição o limite da função quando x tende a 0 dá menos infinito:

$\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=-\infty \ \longrightarrow \ \lim_{x\to 0}f(x)=-\infty$

Observe que se os limites laterais tivessem dado valores diferentes, o limite da função neste ponto não existiria.

Zero entre zero indeterminação

O limite indeterminado zero dividido por zero é muito comum e é obtido em funções com frações em que o numerador e o denominador se cancelam.

$\cfrac{0}{0}$

Este tipo de limite indeterminado é resolvido de forma diferente dependendo da função. Por exemplo, se a função tiver raízes, diferentes etapas deverão ser executadas. Você pode ver as diferentes resoluções deste tipo de indeterminação no seguinte link:

➤ Veja: como resolver a indeterminação do zero entre zero

Indeterminação infinita entre o infinito

A indeterminação infinita entre o infinito geralmente ocorre nos limites infinitos de funções com frações. Embora a indeterminação seja o quociente de dois infinitos, o resultado não precisa necessariamente ser infinito.

$\cfrac{\infty}{\infty}$

Este tipo de forma indeterminada é resolvida por comparação. Ou seja, observa-se o grau do numerador e o grau do denominador e, dependendo de qual for maior, o resultado limite é um ou outro. Você pode ver todos os casos no seguinte link:

➤ Veja: exercícios resolvidos sobre limites infinitos entre o infinito

Indeterminação 1 elevada ao infinito

Matematicamente, pode-se pensar que 1 ao infinito dá 1, já que qualquer potência de 1 é igual a 1. Contudo, este termo é uma indeterminação e, portanto, não se pode deduzir o seu resultado tão facilmente.

$1^{\infty}$

Este tipo de indeterminação é calculado aplicando a seguinte fórmula:

$\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}$

Por exemplo, o seguinte limite é indeterminado porque dá a potência do infinito:

$\displaystyle\lim_{x\to+\infty}\left(1-\frac{1}{x}\right)^x=\left(1-\frac{1}{+\infty}\right)^{+\infty}=(1-0)^{+\infty}=1^{+\infty}$

Devemos, portanto, utilizar a fórmula para este tipo de indeterminação:

$\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}$

E assim já resolvemos o limite indeterminado elevado ao infinito.

Indeterminação zero trazida a zero

A indeterminação zero elevada à potência zero aparece dentro dos limites de funções complicadas.

$0^0$

Para resolver esse tipo de limite indeterminado, você deve usar a seguinte propriedade de limite:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Por exemplo, o limite a seguir dá a forma indeterminada 0 elevado à potência de 0:

$\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=\left(\frac{1}{+\infty}\right)^{\frac{1}{+\infty}}=0^0$

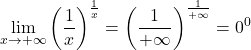
Mas se aplicarmos logaritmos ao limite, podemos encontrar o seu valor:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}$

Indeterminação zero para o infinito

É difícil encontrar a indeterminação do produto de zero e infinito , mas isso não significa que seja fácil de determinar.

$0\cdot \infty$

Não existe um método único para resolver este tipo de indeterminação, mas depende do tipo de função. Neste caso, devemos transformar a função em indeterminação infinita dividida por infinito ou indeterminação zero dividida por zero, e a partir daí aplicar os métodos de solução que vimos acima para cada indeterminação.

Portanto, se o limite de uma função for 0 e o limite da outra função for ∞:

$\displaystyle\lim_{x\to a}f(x)=0\qquad\lim_{x\to a}g(x)=\infty$

Podemos transformar esse tipo indefinidamente fazendo as seguintes alterações:

$\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}$

Vamos ver como fazer isso resolvendo um limite indeterminado como exemplo:

$\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=e^{-\infty}\cdot (+\infty)=0\cdot \infty$

Operamos na função para obter indeterminação infinita sobre o infinito e então encontramos o limite:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}$

Indeterminação zero elevada ao infinito

A indeterminação zero elevada ao infinito é um pouco difícil de entender, pois estamos elevando um número muito pequeno a um número muito grande.

$0^{\infty}$

Quando essas formas indeterminadas são obtidas, deve-se utilizar a seguinte fórmula:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Vamos resolver um exemplo para entender melhor como calcular esse tipo de indeterminação:

$\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}$

Indeterminação infinita levada a zero

Normalmente, qualquer potência elevada a zero dá 1, porém, a indeterminação do infinito elevada a zero não precisa necessariamente ser assim.

$\infty^0$

Assim como nas indeterminações zero elevado a zero e zero elevado ao infinito, para resolver este tipo de limite indeterminado é necessário aplicar logaritmos:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Vamos ver como esse tipo de limites indeterminados é resolvido calculando um exemplo passo a passo:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}$

Tipos de indeterminações (limites indeterminados)

O que são indeterminações?

Tipos de indeterminações

Infinito menos indeterminação infinita

Número de indeterminação entre zero

Zero entre zero indeterminação

Indeterminação infinita entre o infinito

Indeterminação 1 elevada ao infinito

Indeterminação zero trazida a zero

Indeterminação zero para o infinito

Indeterminação zero elevada ao infinito

Indeterminação infinita levada a zero

Deixe um comentário Cancelar resposta