Nesta página explicamos o que é o termo independente de um polinômio e como ele é calculado. Além disso, você poderá ver diversos exemplos de como identificar o termo independente de diferentes polinômios e, ainda, praticar com exercícios resolvidos.
Qual é o termo independente de um polinômio?
A definição do termo independente de um polinômio é a seguinte:
Em matemática, o termo independente de um polinômio é o termo que não possui variável. Portanto, o termo independente de um polinômio corresponde ao monômio de grau zero do polinômio.
Por exemplo, o termo independente do seguinte polinômio é 7:
![]()
No polinômio do exemplo anterior, o termo que não possui parte literal, ou seja, não possui x, é o número 7. Por isso, o termo independente do referido polinômio é 7.
Embora o termo independente de um polinômio pareça um conceito muito simples, saiba que ele é muito útil para alguns cálculos polinomiais. Por exemplo, o procedimento para encontrar as raízes de um polinômio começa no seu termo independente. Se quiser saber mais sobre como encontrar as raízes (ou zeros) de um polinômio, você pode conferir este link, onde também pode ver exemplos e praticar com exercícios resolvidos passo a passo.
Exemplos de termos independentes de polinômios
Depois de sabermos o significado do termo independente de um polinômio, veremos vários exemplos de como encontrar o termo independente de um polinômio:
- Exemplo de termo independente de um polinômio de grau 4:
![]()
O polinômio neste exemplo é um polinômio mônico e o termo que não possui variável é 5, portanto o valor do termo independente do polinômio é 5.
- Exemplo de termo independente de um polinômio de grau 5:
![]()
O elemento deste polinômio que não vem acompanhado da variável x é -2, é portanto o termo independente do polinômio. Observe que o sinal negativo do número também está incluído no termo independente.
- Exemplo de termo independente de um polinômio de grau 8:
![]()
Todos os monômios neste polinômio têm uma variável exceto +1, então o termo independente do polinômio é +1.
Finalmente, uma das propriedades do termo independente é que o valor numérico de um polinômio para x=0 é sempre igual ao seu termo independente. Se você está mais interessado nessa curiosidade, pode consultar na página do link como é calculado o valor numérico de um polinômio, além disso você também encontrará vários exemplos de como isso é feito e poderá praticar com exercícios resolvidos passo a passo.
Exercício resolvido sobre o termo independente de um polinômio
Para finalizar a assimilação do que é o termo independente de um polinômio, sugerimos que você faça o exercício que resolvemos a seguir:
- Dado o polinômio
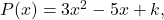
calcula o valor do termo independente

para que fique cheio
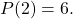
A primeira coisa a fazer para resolver esse problema é tentar determinar
![]()
Ainda:
![]()
Calculamos a potência:
![]()
Fazemos as multiplicações:
![]()
E subtraímos como termos:
![]()
Assim, para que a condição do enunciado seja atendida, é necessário equalizar a expressão algébrica obtida a 6:
![]()
![]()
Portanto, é suficiente resolver a equação resultante:
![]()
![]()
Concluindo, o termo independente do polinômio deve ser 4.
Finalmente, você deve saber que o termo independente de um polinômio também é importante para aplicar corretamente a regra de Ruffini. Caso você não saiba o que é, a regra de Ruffini é um método usado para dividir polinômios rapidamente. Aqui você pode ver como fazer a regra de Ruffini e como ela se relaciona com o termo independente de um polinômio.