Nesta página explicamos o que é o teorema do fator. Além disso, mostramos para que serve o teorema do fator: divisibilidade de polinômios, encontrar raízes, fatorar polinômios, etc. Finalmente, você poderá praticar exercícios passo a passo sobre o teorema do fator.
Qual é o teorema do fator?
Em matemática, o teorema do fator diz que um polinômio P(x) é divisível por outro polinômio da forma (xa) se e somente se P(a)=0.
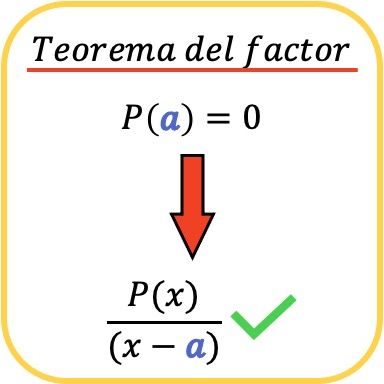
Da mesma forma, como consequência do teorema do fator, segue-se que se um polinômio P(x) é divisível pelo termo (x−a), isso significa que o valor a é uma raiz (ou zero) do polinômio P( x ).
O fato de um polinômio ser divisível por outro significa que o resto (ou resto) da divisão entre os dois polinômios é igual a zero. Caso você não se lembre completamente deste conceito, no link a seguir você poderá ver exemplos de divisão de polinômios , lá você também encontrará a explicação de como dividir polinômios e exercícios resolvidos passo a passo.
Exemplos de teoremas de fator
Agora que conhecemos a definição matemática do teorema do fator, vejamos vários exemplos para ver como ele é aplicado.
Exemplo 1
Uma aplicação do teorema do fator é descobrir se um determinado polinômio é divisível por um binômio . Vejamos um exemplo de como isso é feito com o teorema do fator:
- Determine se o polinômio P(x) é divisível pelo binômio Q(x), sendo ambos:
![]()
Primeiro, o polinômio divisor, Q(x), é um polinômio do tipo (xa), portanto podemos aplicar o teorema do fator para resolver o problema.
Então, para verificar se P(x) pode ser dividido por Q(x) precisamos calcular o valor numérico do polinômio P(x) para x=1, já que 1 é o termo independente do polinômio divisor com seu sinal alterado :
![Rendered by QuickLaTeX.com \begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00216efc4a2e53b0b38de1175e73a5bd_l3.png)
O valor numérico do polinômio P(x) em x = 1 dá zero, então de acordo com o teorema do fator P(x) é divisível por Q(x), ou em outras palavras, o resto da divisão por ambos será nulo.
Podemos verificar que a condição de divisibilidade é satisfeita dividindo os 2 polinômios pelo teorema de Ruffini :
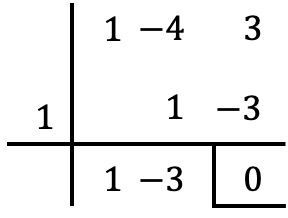
Como você pode ver neste exemplo, o teorema do fator é um caso especial do teorema do resto (ou resto). Deixo para vocês este artigo que explica o que é o teorema do resto , você também encontrará exemplos e exercícios resolvidos com ele. E, além do mais, você poderá ver qual é a diferença entre o teorema do resto e o teorema do fator.
Exemplo 2
O teorema do fator também pode ser usado para encontrar as raízes (ou zeros) de um polinômio. Mas, obviamente, para entender esse tipo de problema é preciso saber quais são as raízes de um polinômio . Se você ainda não entende esse conceito, pode dar uma olhada na página do link, que é explicada detalhadamente.
Então, vamos ver através de um exemplo como o teorema do fator é aplicado para encontrar a raiz de um polinômio:
- Dado o polinômio P(x), calcule se uma de suas raízes é x=2:
![]()
Aplicando o teorema do fator, o termo x=2 só será raiz do polinômio P(x) se o valor numérico de P(x) para x=2 for zero. Portanto, precisamos encontrar este valor numérico:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82d50f0361613cb6c540051f8da4bc20_l3.png)
Na verdade, o valor numérico do polinômio P(x) desaparece em x=2, então graças ao teorema do fator podemos afirmar que x=2 é uma raiz do polinômio P(x).
Fatoração de polinômios usando o teorema do fator
Outra aplicação do teorema do fator é a fatoração de polinômios . Caso você não saiba o que é, fatorar um polinômio significa transformar a expressão de um polinômio em produto de fatores, ou seja, fatorar um polinômio simplifica sua expressão algébrica.
Assim, o teorema fatorial estabelece que se um polinômio P(x) satisfaz P(a)=0 para um determinado valor a, então a expressão desse polinômio pode ser fatorada no produto P(x)=(xa)· Q( x), onde Q(x) é o polinômio resultante da divisão do polinômio P(x) por (xa).
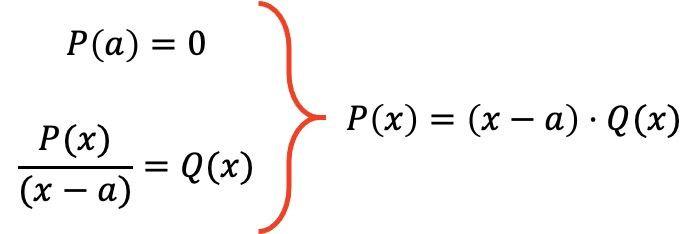
Como exemplo, fatoraremos o seguinte polinômio usando o teorema fatorial:
![]()
Do polinômio anterior, podemos saber que x=-2 é uma de suas raízes, pois o valor numérico do polinômio para x=-2 é igual a zero:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d94a4657a385e672badeabd7458b376_l3.png)
Dividimos portanto com a regra de Ruffini o polinômio P(x) entre o binômio formado por x e esta raiz mudou de sinal, ou seja, o fator (x+2):
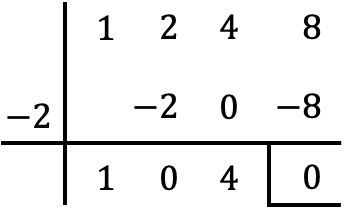
Portanto, o quociente da divisão polinomial é:
![]()
E finalmente, a partir do teorema do fator, podemos expressar o polinômio P(x) na forma de uma multiplicação do fator (x+2) pelo quociente obtido na divisão anterior:
![]()
Assim, fatoramos o polinômio P(x), mas apenas parcialmente. Para fatorar completamente um polinômio, um procedimento mais longo deve ser aplicado. Fizemos um guia onde ensinamos passo a passo como fatorar polinômios de Ruffini , além disso, neste artigo explicamos todos os tipos de fatorações e você poderá praticar com exercícios resolvidos. Então clique no link para descobrir como fatorar um polinômio do conjunto.
Problemas resolvidos do teorema do fator
A seguir, preparamos diversos exercícios resolvidos passo a passo sobre o teorema do fator para que você possa praticar, e assim verificar se entendeu este teorema. Recomendamos que você tente fazer isso sozinho e veja se entendeu a solução corretamente. Não se esqueça também que você pode nos deixar suas dúvidas abaixo nos comentários! ❓❓💬💬
Exercício 1
Use o teorema fatorial para descobrir se o polinômio P(x) é divisível pelo binômio Q(x) e, em caso afirmativo, encontre uma raiz do polinômio e fatore-a.
![]()
Neste caso, o divisor polinomial Q(x) é um binômio composto apenas por um x e um termo independente. Então, para mostrar que o polinômio P(x) pode ser dividido pelo outro polinômio Q(x) com o teorema fatorial, devemos avaliar o valor numérico do polinômio P(x) no termo independente do polinômio divisor de sinal alterado, isto é, em x = 3:
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e8ac752f8e16fae1d66386e9d2a02a0_l3.png)
O valor numérico do polinômio P(x) em x=3 é equivalente a 14, ou seja, é diferente de zero. Portanto, de acordo com o teorema do fator, P(x) NÃO é divisível por Q(x) porque o resto da divisão não é zero.
Exercício 2
Descubra pelo teorema fatorial se o polinômio P(x) é divisível pelo binômio Q(x) e, em caso afirmativo, encontre uma raiz do polinômio P(x) e fatore-o.
![]()
Neste caso o divisor polinomial Q(x) é um binômio composto apenas por um x e um termo independente, podemos portanto aplicar o teorema fatorial.
E para verificar se o polinômio P(x) pode ser dividido pelo polinômio Q(x), devemos encontrar o valor numérico do polinômio P(x) para o termo independente do polinômio Q(x) mudou de sinal, é ou seja, em x=-1:
![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34b63772a1b44bee2c746d94b6ca4785_l3.png)
Neste problema, o valor numérico do polinômio em x=-1 é zero, então P(x) é divisível por Q(x).
Então, podemos deduzir pelo teorema fatorial que x=-1 é uma raiz do polinômio P(x), pois o valor numérico de P(x) em x=-1 desaparece.
Assim, como x=-1 é raiz do polinômio P(x), para fatorá-lo, basta dividi-lo por x+1. E, para isso, vamos utilizar o método Ruffini:
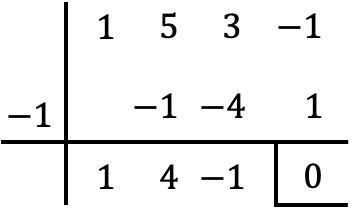
Então o resultado da operação é:
![]()
Podemos, portanto, fatorar o polinômio P(x) da seguinte forma:
![]()
Exercício 3
Descubra com o teorema fatorial se o polinômio P(x) é divisível pelo binômio Q(x) e, em caso afirmativo, encontre também uma raiz do polinômio P(x) e fatore-a.
![]()
Neste caso, o polinômio que divide Q(x) é um binômio formado apenas por um x e um termo independente, portanto podemos utilizar o teorema do fator.
E para verificar se o polinômio P(x) é divisível pelo polinômio Q(x), devemos determinar o valor numérico do polinômio P(x) para o termo independente do polinômio Q(x) mudou de sinal, ou seja- ou seja, em x = -3:
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef8bb895fe041193d71351ffadb94f2f_l3.png)
Neste caso, o valor numérico do polinômio em x=-3 é zero, então de fato P(x) é divisível por Q(x).
Por isso, deduzimos do teorema fatorial que x=-3 é raiz do polinômio P(x), pois P(-3) é igual a zero.
Então, como x=-3 é raiz do polinômio P(x), para fatorá-lo devemos dividi-lo por x+3. E, para isso, utilizaremos a regra de Ruffini:
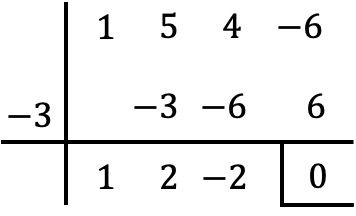
Então o resultado da divisão é:
![]()
E, portanto, podemos fatorar o polinômio P(x) da seguinte maneira:
![]()
O que você acha do teorema do fator? Você acha que é útil em álgebra? Nós lemos você nos comentários!
👀⬇⬇⬇👀