Neste artigo você encontrará a definição do teorema de Weierstrass. Além disso, você poderá praticar diversos exercícios resolvidos passo a passo do teorema de Weierstrass para entendê-lo perfeitamente.
Declaração do teorema de Weierstrass
O teorema de Weierstrass diz que se uma função é contínua num intervalo fechado, essa função tem um máximo absoluto e um mínimo absoluto nesse intervalo.
➤ Veja: O que é uma função contínua?
O teorema de Weierstrass afirma apenas que existe um máximo e um mínimo, mas não é útil calcular os valores desses pontos.
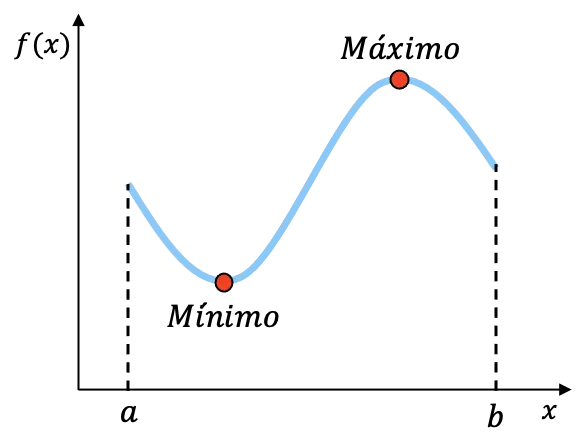
Por exemplo, a função representada graficamente acima é contínua no intervalo [a,b] e tem um mínimo e um máximo neste intervalo. Embora não possamos saber as coordenadas exatas destes dois pontos, sabemos que a função tem estes dois pontos finais no intervalo.
➤ Veja: como calcular o máximo e o mínimo de uma função
Como a função é contínua ao longo de todo o intervalo, isso significa que ela também assumirá todos os valores possíveis entre o mínimo absoluto e o máximo absoluto nesse mesmo intervalo.
Além disso, como consequência do teorema de Weierstrass, pode-se deduzir que qualquer função contínua em um intervalo fechado é limitada acima e abaixo de , e os limites superior e inferior da função são o máximo e o mínimo absolutos, respectivamente.
Matematicamente, o teorema de Weierstrass pode ser expresso da seguinte forma:
Ouro
E
são dois pontos incluídos (o mínimo absoluto e o máximo absoluto respectivamente) no intervalo fechado
![[a,b]](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png "Rendered by QuickLaTeX.com")
em que a função é definida.
A prova do teorema de Weierstrass é bastante complicada e não contribui muito para o conceito, por isso não a explicaremos neste artigo. O importante é que você entenda o que é o teorema de Weierstrass e para que serve.
Problemas resolvidos pelo teorema de Weierstrass
Exercício 1
Determine se a seguinte função está limitada ao intervalo proposto:
![f(x)=\log_3(x-4) \qquad x \in [5,10]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e6a705ea1c5d586cf31d683ac7ccc85_l3.png "Rendered by QuickLaTeX.com")
➤ Veja: domínio de uma função logarítmica
Podemos determinar se a função é limitada no intervalo [5,10] aplicando o teorema de Weierstrass. Devemos portanto saber se a função é contínua neste intervalo, para isso calculamos o domínio da função logarítmica:
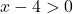
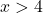
A função é contínua para todos os valores maiores que x=4, portanto é contínua no intervalo [5,10].
Portanto, a função satisfaz o teorema de Weierstrass no intervalo [5,10], o que significa que ela é limitada acima e abaixo deste intervalo.
Exercício 2
Determine se a seguinte função tem máximo e/ou mínimo no intervalo proposto:
![f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f2e72f629bae2c39821ddbfbf6c93fc_l3.png "Rendered by QuickLaTeX.com")
➤ Veja: domínio de uma função racional
Primeiro, analisamos a continuidade da função racional:
Porém, a função apresenta uma descontinuidade em x=2, o que implica que ela não é contínua no intervalo [-3,3].
Resumindo, a função não satisfaz o teorema de Weierstrass e por isso não podemos dizer se tem mínimo ou máximo neste intervalo.
Exercício 3
Determine se a seguinte função tem máximo e/ou mínimo no intervalo proposto e calcule estes pontos:
![f(x)=x^2+3 \qquad x \in [0,4]](https://mathority.org/wp-content/ql-cache/quicklatex.com-4dd0cf4151f8b5c1b4e69be89b7a71e1_l3.png "Rendered by QuickLaTeX.com")
➤ Veja: características das funções quadráticas
O domínio de qualquer função quadrática são todos os números reais:
A função é, portanto, contínua no intervalo [0,4] e satisfaz o teorema de Weierstrass. A função, portanto, tem um mínimo absoluto e um máximo absoluto neste intervalo.
Além disso, o vértice desta parábola está exatamente em x=0, então a função é estritamente crescente no intervalo [0,4] e, conseqüentemente, o mínimo está em x=0 e o máximo em x= 4 .
Karl Weierstrass
Depois de vermos o que significa o teorema de Weierstrass, explicaremos brevemente quem foi o inventário deste teorema.
Karl Theodor Wilhelm Weierstrass foi um matemático alemão muito importante do século XIX, mais precisamente, nasceu em 31 de outubro de 1815 em Ostenfelde e morreu em 19 de fevereiro de 1897 em Berlim.
Além do teorema de Weierstrass, ele também é conhecido por suas outras contribuições à matemática. Entre eles, deu as definições de continuidade, limite e derivada, três conceitos de funções muito importantes.
Da mesma forma, conseguiu demonstrar certos teoremas que ainda não eram verificados matematicamente naquela época, como o teorema de Bolzano-Weierstrass, o teorema do valor médio ou o teorema de Heine-Borel.
Como curiosidade, existe uma cratera lunar e um asteroide com o nome de Weierstrass em sua homenagem.