Teorema de Rouche-Frébenius

Nesta página descobriremos o que é o teorema de Rouché Frobenius e como calcular o posto de uma matriz com ele. Você também encontrará exemplos e exercícios resolvidos passo a passo com o teorema de Rouché-Frobenius.

Qual é o teorema de Rouché-Frobenius?

O teorema de Rouché-Frobenius é um método para classificar sistemas de equações lineares. Em outras palavras, o teorema de Rouché-Frobenius é usado para descobrir quantas soluções um sistema de equações tem sem precisar resolvê-lo.

Existem 3 tipos de sistemas de equações:

Compatível com Sistema Determinado (SCD): O sistema possui uma solução única.
Sistema compatível indeterminado (ICS): o sistema possui infinitas soluções.
Sistema Incompatível (SI): O sistema não tem solução.

Além disso, o teorema de Rouché-Frobenius também nos permitirá mais tarde resolver sistemas usando a regra de Cramer .

Declaração do teorema de Rouché-Frobenius

O teorema de Rouché-Frobenius diz que

$\displaystyle \bm{A}$

é a matriz formada pelos coeficientes das incógnitas de um sistema de equações. e a barriga

$\displaystyle \bm{A'}$

, ou matriz estendida , é a matriz formada pelos coeficientes das incógnitas de um sistema de equações e pelos termos independentes:

O teorema de Rouché-Frobenius permite-nos saber com que tipo de sistema de equações estamos lidando de acordo com o posto das matrizes A e A’:

Se classificação(A) = classificação(A’) = número de incógnitas ⟶ Sistema compatível determinado (SCD)
Se classificação (A) = classificação (A’) < número de incógnitas ⟶ Sistema compatível indeterminado (SCI)
se intervalo (A)
$\bm{\neq}$

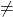
faixa (A’) ⟶ Sistema incompatível (SI)

Assim que soubermos o que diz o teorema de Rouché-Frobenius, veremos como resolver os exercícios do teorema de Rouché-Frobenius. Aqui estão 3 exemplos: um exercício resolvido usando o teorema de cada tipo de sistema de equações.

Exemplo de sistema compatível determinado (SCD)

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

A matriz A e a matriz estendida A’ do sistema são:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

Calculamos agora a classificação da matriz A. Para isso, verificamos se o determinante de toda a matriz é diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

Como a matriz tem um determinante 3×3 diferente de 0, a matriz A tem posto 3:

$\displaystyle rg(A)=3$

Uma vez conhecida a classificação de A, calculamos a classificação de A’, que será pelo menos a classificação 3 porque acabamos de ver que tem dentro de si um determinante de ordem 3 diferente de 0. além disso, não pode ser de classificação 4, já que não podemos fazer nenhum determinante de ordem 4. Portanto, a matriz A’ também é de posto 3:

$\displaystyle rg(A')=3$

Assim, como o posto da matriz A é igual ao posto da matriz A’ e ao número de incógnitas do sistema (3), sabemos pelo teorema de Rouché Frobenius que se trata de um Sistema Determinado Compatível (SCD) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Exemplo de um sistema compatível indeterminado (ICS)

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

A matriz A e a matriz estendida A’ do sistema são:

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

Calculamos agora a classificação da matriz A. Para isso, verificamos se o determinante de toda a matriz é diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

O determinante de toda a matriz A dá 0, portanto não é de posto 3. Para ver se é de posto 2, devemos encontrar uma submatriz em A cujo determinante seja diferente de 0. Por exemplo, aquele do canto superior esquerdo :

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Como a matriz tem um determinante 2×2 diferente de 0, a matriz A tem posto 2:

$\displaystyle rg(A)=2$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis:

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

Todos os determinantes 3×3 da matriz A’ são 0, então a matriz A’ também não terá classificação 3. Porém, dentro dele possui determinantes de ordem 2 diferentes de 0. Por exemplo:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Portanto , a matriz A’ será de classificação 2 :

$\displaystyle rg(A')=2$

A extensão da matriz A é igual à extensão da matriz A’ mas estes são menores que o número de incógnitas do sistema (3). Portanto, segundo o teorema de Rouché-Frobenius, trata-se de um sistema compatível indeterminado (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Exemplo de sistema incompatível (IS)

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

A matriz A e a matriz estendida A’ do sistema são:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

Calculamos agora a classificação da matriz A. Para isso, verificamos se o determinante de toda a matriz é diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

Como a matriz possui um determinante de ordem 2 diferente de 0, a matriz A é de posto 2:

$\displaystyle rg(A)=2$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, então agora tentamos, por exemplo, com o determinante das 3 últimas colunas:

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

Por outro lado, a matriz A’ contém um determinante cujo resultado é diferente de 0, portanto a matriz A’ terá classificação 3 :

$\displaystyle rg(A')=3$

Portanto, como o posto da matriz A é menor que o posto da matriz A’, deduzimos do teorema de Rouché-Frobenius que se trata de um Sistema Incompatível (SI) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Problemas resolvidos do teorema de Rouché-Frobenius

Exercício 1

Determine o tipo do seguinte sistema de equações com 3 incógnitas usando o teorema de Rouché-Frobenius:

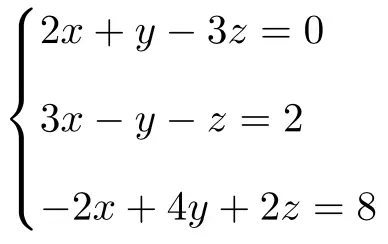
Exercício resolvido do teorema de Rouche - frobenius

veja solução

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

Devemos agora encontrar o posto da matriz A. Para isso, verificamos se o determinante da matriz é diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

A matriz tendo um determinante de terceira ordem diferente de 0, a matriz A tem classificação 3:

$\displaystyle rg(A)=3$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. Este será pelo menos de posto 3, porque acabamos de ver que tem dentro de um determinante de ordem 3 diferente de 0. Além disso, não pode ser de posto 4, pois não podemos deixar de fazer um determinante 4×4. Portanto, a matriz A’ também é de posto 3:

$\displaystyle rg(A')=3$

Assim, graças ao teorema de Rouché-Frobenius, sabemos que se trata de um sistema determinado compatível (SCD), pois o contradomínio de A é igual ao contradomínio de A’ e ao número de incógnitas.

Exercício 2

Classifique o seguinte sistema de equações com 3 incógnitas usando o teorema de Rouché-Frobenius:

veja solução

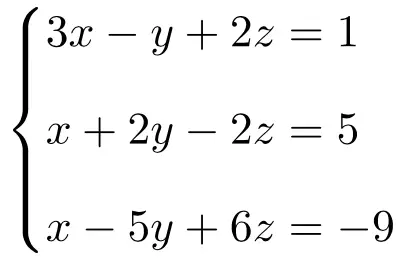
Primeiro construímos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

Agora vamos calcular o intervalo da matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

Portanto, a matriz A tem classificação 2:

$\displaystyle rg(A)=2$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis:

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

Todos os determinantes 3×3 da matriz A’ são 0, então a matriz A’ também não terá classificação 3. Porém, dentro dele possui muitos determinantes de ordem 2 diferentes de 0. Por exemplo:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

Portanto , a matriz A’ será de classificação 2 :

$\displaystyle rg(A')=2$

O posto da matriz A é igual ao posto da matriz A’ mas estes dois são menores que o número de incógnitas do sistema (3). Portanto, pelo teorema de Rouché-Frobenius sabemos que se trata de um sistema compatível indeterminado (ICS):

Exercício 3

Determine que tipo de sistema é o seguinte sistema de equações usando o teorema de Rouché-Frobenius:

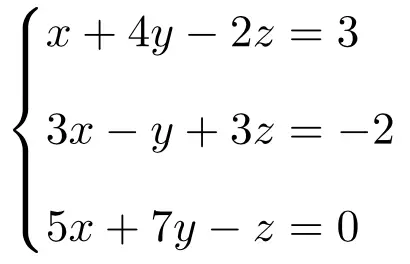
exercício resolvido passo a passo do teorema de rouche - frobenius

veja solução

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

Agora vamos calcular o intervalo da matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

Portanto, a matriz A tem classificação 2:

$\displaystyle rg(A)=2$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, mas não o determinante das 3 últimas colunas:

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

Portanto, a matriz A’ tem classificação 3 :

$\displaystyle rg(A')=3$

O posto da matriz A é menor que o posto da matriz A’, podemos portanto deduzir do teorema de Rouché-Frobenius que se trata de um Sistema Incompatível (SI) :

Exercício 4

Determine o tipo do seguinte sistema de equações com 3 incógnitas usando o teorema de Rouché-Frobenius:

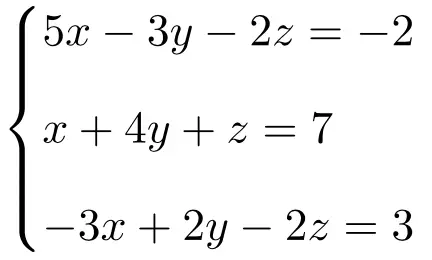
Rouche - Teorema de Frobenius resolveu exercício com 3 incógnitas e 3 equações

veja solução

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

Devemos agora calcular a classificação da matriz A. Para fazer isso, resolvemos o determinante da matriz com a regra de Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

A matriz tendo um determinante de terceira ordem diferente de 0, a matriz A tem classificação 3:

$\displaystyle rg(A)=3$

Portanto, a matriz A’ também é de posto 3 , pois é sempre pelo menos de posto A e não pode ser de posto 4 porque não podemos resolver nenhum determinante 4×4.

$\displaystyle rg(A')=3$

Assim, graças à aplicação do teorema de Rouché-Frobenius, sabemos que o sistema é um Sistema Determinado Compatível (SCD), pois o contradomínio de A é igual ao contradomínio de A’ e ao número de incógnitas.

Exercício 5

Identifique que tipo de sistema é o seguinte sistema de equações usando o teorema de Rouché-Frobenius:

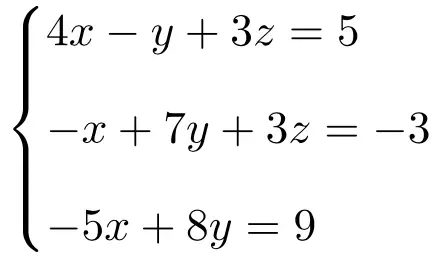
exemplo do teorema de Rouche - frobenius

veja solução

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

Agora vamos calcular o intervalo da matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

A matriz A é, portanto, de classificação 2:

$\displaystyle rg(A)=2$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. O determinante das 3 primeiras colunas que já conhecemos dá 0, mas o determinante das 3 últimas colunas não dá:

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

Portanto, a matriz A’ tem classificação 3 :

$\displaystyle rg(A')=3$

E, por fim, aplicamos o domínio ao teorema de Rouché-Frobenius: o domínio da matriz A é menor que o domínio da matriz A’, é portanto um Sistema Incompatível (SI) :

Exercício 6

Classifique o seguinte sistema de equações de ordem 3 com o teorema de Rouché-Frobenius:

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

veja solução

Primeiro construímos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

Agora vamos calcular o intervalo da matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Portanto, a matriz A tem classificação 2:

$\displaystyle rg(A)=2$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis:

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

Todos os determinantes 3×3 da matriz A’ são 0, então a matriz A’ também não terá classificação 3. Porém, dentro dele possui determinantes de ordem 2 diferentes de 0. Por exemplo:

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Portanto , a matriz A’ será de classificação 2 :

$\displaystyle rg(A')=2$

Finalmente, aplicando o teorema de Rouché-Frobenius, sabemos que se trata de um Sistema Compatível Indeterminado (ICS), pois o contradomínio da matriz A é igual ao contradomínio da matriz A’ mas estes dois são menores que o número de incógnitas no sistema (3):

Teorema de rouche-frébenius

Qual é o teorema de Rouché-Frobenius?

Declaração do teorema de Rouché-Frobenius

Exemplo de sistema compatível determinado (SCD)

Exemplo de um sistema compatível indeterminado (ICS)

Exemplo de sistema incompatível (IS)

Problemas resolvidos do teorema de Rouché-Frobenius

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Deixe um comentário Cancelar resposta