▷ Taxa de variação média e instantânea (exercícios resolvidos)

Aqui explicamos o que são taxa de mudança, taxa média de mudança e taxa de mudança instantânea. Você poderá ver vários exemplos de como calcular a taxa de variação e, além disso, poderá praticar com exercícios passo a passo resolvidos sobre a taxa de variação.

Qual é a taxa de mudança?

Em matemática, a taxa de variação (TV) de uma função é a diferença nos valores de uma função em dois pontos diferentes. Portanto, para calcular a taxa de variação entre dois pontos, os valores da função nesses dois pontos devem ser subtraídos.

$\text{TV}[a,b]=f(b)-f(a)$

Por exemplo, se duas imagens de uma função são f(2)=1 e f(5)=7, sua taxa de variação é:

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

Acabamos de ver o significado matemático de taxa de variação, mas em economia o conceito de taxa de variação significa o seguinte:

Em economia, a taxa de variação entre dois valores é a diferença entre eles expressa em percentagem, ou seja, a taxa de variação de uma variável entre diferentes períodos é a sua variação relativa. Portanto, para calcular a taxa de variação, subtraem-se os valores dos dois períodos distintos e o resultado obtido é dividido pelo valor do período inicial.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

Por exemplo, se o valor de determinadas ações aumentou de 35€ para 50€ num mês, a sua taxa de variação será:

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

Considerando os dois significados possíveis de taxa de variação, neste artigo nos concentraremos na compreensão da definição matemática de taxa de variação. Dois tipos de taxa de variação podem ser distinguidos: a taxa de variação média e a taxa de variação instantânea. Abaixo você tem a explicação de cada tipo.

Taxa média de mudança

A taxa média de variação (TVM) de uma função em um intervalo é o número de unidades que a função aumenta (ou diminui) para cada unidade que sua variável independente aumenta. Portanto, a taxa média de variação de uma função é calculada dividindo o crescimento da função em um intervalo pela amplitude desse mesmo intervalo.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

Para que você possa ver como é calculada a taxa média de variação, resolvemos um exemplo passo a passo abaixo.

Exemplo de cálculo da taxa média de variação de uma função

Calcule a taxa média de variação no intervalo [2.5] da seguinte função:

$f(x) = x^2-1$

Primeiro, calculamos o valor da função em x=2 e x=5:

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

E então calculamos a taxa média de variação da função no intervalo simplesmente aplicando a fórmula:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

Como o resultado de TVM[2,5] é positivo, isso significa que a função cresce no intervalo [2,5]. Por outro lado, se o resultado tivesse sido negativo, isso significaria que a função diminui neste intervalo.

Interpretação geométrica da taxa média de mudança

Geometricamente, a taxa média de variação de uma função em um intervalo representa a inclinação da reta que une os pontos extremos do intervalo.

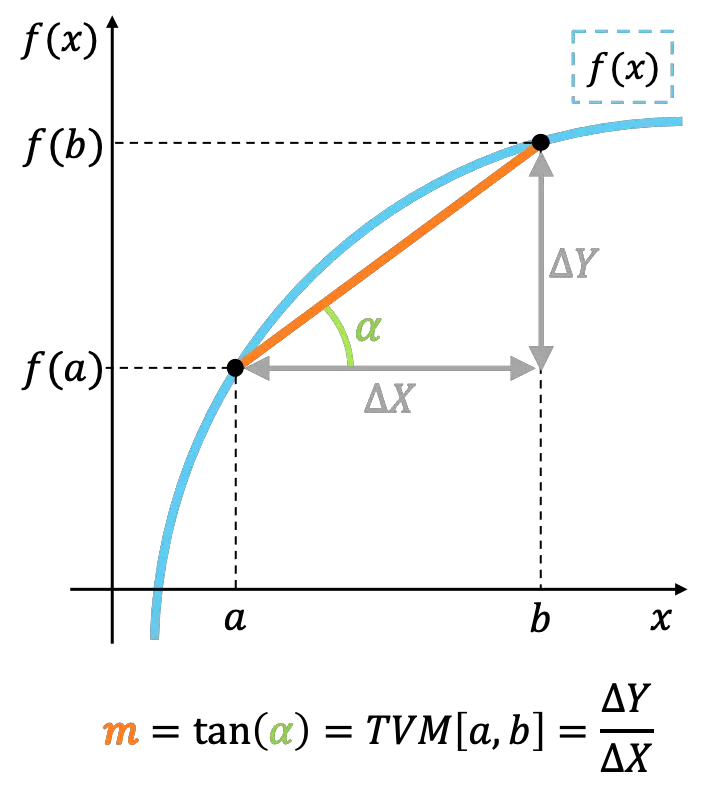
Taxa instantânea de mudança

A taxa de variação instantânea (TVI) de uma função em um ponto é o limite infinitesimal do aumento relativo da função ao longo de um intervalo. Portanto, a taxa instantânea de mudança é calculada resolvendo o limite do quociente de f(a+h)-f(a) quando h se aproxima de zero.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

O valor da taxa de variação instantânea pode ser positivo, negativo ou zero, e significa que a função naquele ponto está aumentando, diminuindo ou permanecendo a mesma, respectivamente, naquele ponto.

Exemplo de cálculo da taxa instantânea de variação de uma função

Calcule a taxa instantânea de variação no ponto x=2 da seguinte função:

$f(x) = x^2$

Para calcular a taxa de variação instantânea, precisamos aplicar a fórmula:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

Resolvemos a identidade notável:

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ Se você não se lembra mais das fórmulas para identidades notáveis , encontrará todas as fórmulas em nosso site especializado em polinômios: www.polinomios.org

Agora vamos tentar resolver o limite:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

Mas encontramos indeterminação zero entre zero, portanto:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ Veja: como resolver um limite com indeterminação de zero entre zero

E finalmente resolvemos o limite:

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

Ainda:

$\mathbf{TVI} \bm{(2) = 4}$

Como o resultado de TVI(2) é positivo, isso significa que a função aumenta em x=2. Por outro lado, se o resultado tivesse sido negativo, isso significaria que a função está diminuindo nesta fase.

Interpretação geométrica da taxa instantânea de mudança

Geometricamente, a taxa instantânea de variação de uma função em um ponto representa a inclinação da reta tangente à função nesse mesmo ponto.

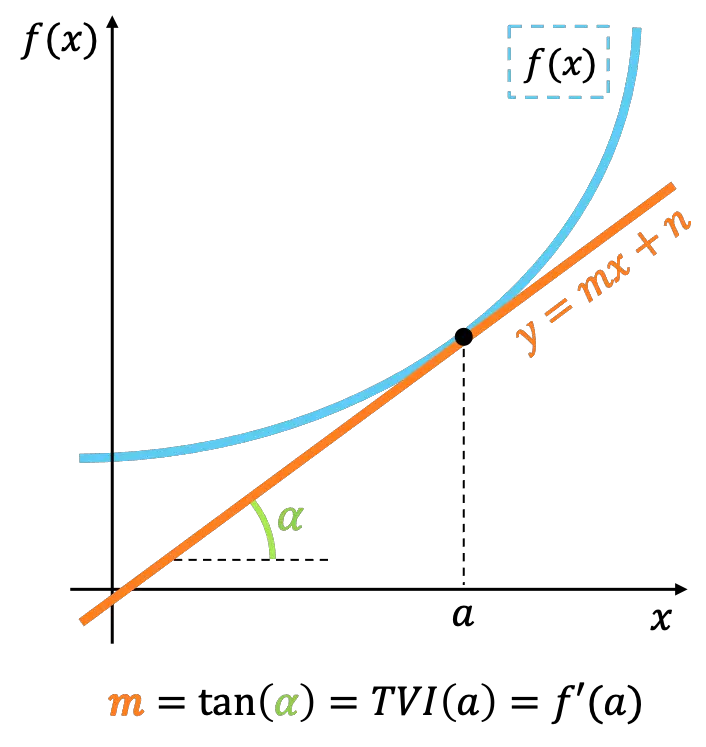
Se você olhar de perto, o significado de taxa de variação instantânea é equivalente ao conceito de derivada de uma função . Assim, a taxa de variação instantânea também é usada para calcular o valor da derivada de uma função em um ponto.

Exercícios resolvidos sobre taxa de variação

Exercício 1

Calcule o valor da taxa de variação da seguinte função no intervalo [1,3].

$f(x)=x^2-5$

Veja a solução

Primeiro, determinamos o valor da função nas extremidades do intervalo:

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

E agora aplicamos a fórmula da taxa de variação:

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

Exercício 2

Calcule a taxa média de variação (TVM) da seguinte função no intervalo [1,4]:

$f(x)=2x+1$

Veja a solução

Primeiro calculamos as imagens da função em x=1 ex=4.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

E aplicamos a fórmula para a taxa média de variação:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

Exercício 3

Encontre a taxa média de variação da seguinte função no intervalo [-1,3]:

$f(x)=(x+1)^2$

Veja a solução

Para determinar a taxa média de mudança, primeiro precisamos calcular f(-1) e f(3):

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

Agora usamos a fórmula para a taxa média de variação:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

Exercício 4

Calcule a taxa média de variação no intervalo [2,4] da função mostrada no gráfico a seguir:

Veja a solução

Aplicamos a fórmula para a taxa média de variação:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

Como vemos na fórmula, precisamos encontrar o valor de f(4) e f(2). E isso pode ser feito facilmente observando a representação gráfica da função:

$f(4)=5$

$f(2)=1$

E agora que conhecemos os valores da função, substituímos-os na fórmula:

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

Exercício 5

Calcule a taxa instantânea de variação da seguinte função no ponto x=2:

$f(x)=3x$

Veja a solução

Para determinar a taxa instantânea de variação da função no ponto x=2 aplicamos sua fórmula correspondente:

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

Exercício 6

Determine a taxa de variação instantânea (TVI) da seguinte função no ponto x=1:

$f(x)=x^2+1$

Veja a solução

Aplicamos a fórmula para a taxa de variação instantânea:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

Então, calculamos

$f(1+h)$

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

E substituímos os valores encontrados no limite:

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

Resolvemos o produto notável:

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

Agora vamos tentar resolver o limite:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

Mas encontramos a forma indeterminada zero dividido por zero, então fatoramos o polinômio do numerador da fração e simplificamos:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ Se você não sabe como resolver a indeterminação de zero entre zero , pode ver a explicação completa no link acima sobre como resolver um limite com indeterminação de zero entre zero.

E finalmente, resolvemos o limite:

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

Em resumo, a taxa instantânea de variação da função no ponto x=1 é igual a 2.

$\mathbf{TVI} \bm{(1) = 2}$

Exercício 7

Encontre a taxa de variação instantânea da seguinte função no ponto x=2:

$f(x)=4x^2-x+3$

Veja a solução

Primeiro usamos a fórmula da taxa de variação instantânea:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

Nós calculamos

$f(2+h)$

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

E substituímos os valores encontrados no limite:

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

Calculamos a igualdade notável:

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

Operamos no numerador:

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

Agora vamos tentar resolver o limite:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

Mas obtemos a indeterminação zero dividida por zero, então fatoramos os polinômios e simplificamos:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

E finalmente, resolvemos o limite:

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

Ainda:

$\mathbf{TVI} \bm{(2) = 15}$

Taxa média e instantânea de mudança

Qual é a taxa de mudança?

Taxa média de mudança

Exemplo de cálculo da taxa média de variação de uma função

Interpretação geométrica da taxa média de mudança

Taxa instantânea de mudança

Exemplo de cálculo da taxa instantânea de variação de uma função

Interpretação geométrica da taxa instantânea de mudança

Exercícios resolvidos sobre taxa de variação

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Exercício 7

Deixe um comentário Cancelar resposta