Triângulo de Tartaglia (ou Pascal)

Nesta página explicamos o que é o triângulo de Tartaglia, também chamado de triângulo de Pascal. Aprendemos como construir matematicamente o triângulo de Tartaglia (ou Pascal), bem como para que serve e quais são todas as suas propriedades. Finalmente, mostramos como e quando este triângulo tão importante surgiu.

O que é o triângulo de Tartaglia (ou Pascal)?

O triângulo de Tartaglia , também chamado de triângulo de Pascal , é uma representação matemática de inteiros ordenados na forma de um triângulo. O triângulo Tartaglia (ou Pascal) é usado para fazer cálculos matemáticos.

Esta é a definição do triângulo de Tartaglia ou Pascal, mas certamente você entende melhor o conceito com uma imagem do triângulo:

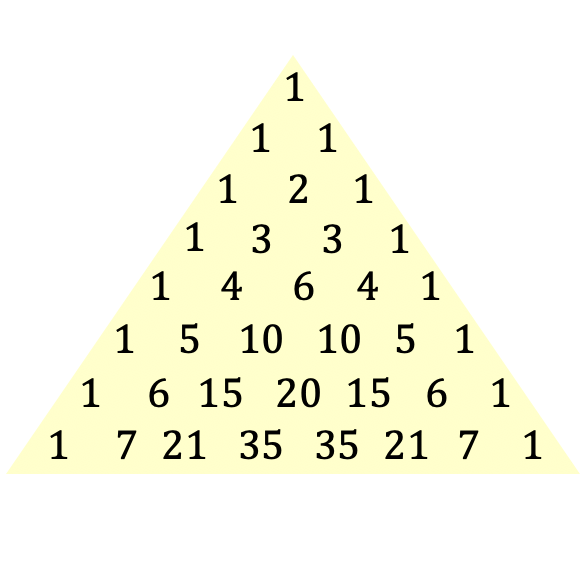
O triângulo de Tartaglia também é chamado de triângulo de Pascal em homenagem ao filósofo e matemático francês Blaise Pascal, que introduziu esta expressão triangular em 1654, embora este triângulo já seja conhecido desde os tempos antigos. A seguir, nos aprofundaremos na história desse triângulo específico.

Como é construído o triângulo de Tartaglia ou Pascal?

Como você viu no triângulo de Pascal (ou Tartaglia), existem muitos números, mas isso não significa que devamos saber de cor (graças a Deus). Existe uma fórmula que permite encontrar facilmente todos os números do triângulo de Pascal ou Tartaglia, bastando resolver somas simples.

Para construir o triângulo de Tartaglia ou Pascal, você começa no topo do triângulo, que é sempre 1, e então as linhas abaixo são calculadas. Cada número nas linhas seguintes é a soma dos dois números diretamente acima dele, exceto as extremidades das linhas que são sempre 1.

Portanto, você pode calcular quantas linhas do triângulo de Tartaglia quiser, pois pode adicionar linhas sucessivamente somando os números.

Para que serve o triângulo de Tartaglia ou Pascal?

Saber construir o triângulo de Tartaglia é muito bom, mas… para que serve esse triângulo aritmético? Pois bem, o triângulo de Tartaglia (ou de Pascal) tem muitas aplicações em matemática, especialmente na área de álgebra.

números combinatórios

Em primeiro lugar, o triângulo de Tartaglia é usado para calcular diretamente números combinatórios , também chamados de coeficientes binomiais. Se não sabe o que são estes tipos de operações, pode procurá-las no nosso site (temos um motor de busca no canto superior direito) porque escrevemos um artigo detalhado onde explicamos como são resolvidas e você aí Você também encontrará exemplos e exercícios resolvidos passo a passo. Mas, em resumo, a expressão algébrica para um número combinatório é a seguinte:

$\displaystyle \begin{pmatrix} n \\ k \end{pmatrix}$

Pois bem, todos os números combinatórios podem ser facilmente determinados com o triângulo de Tartaglia, pois a solução de cada coeficiente binomial é equivalente a um número desta expressão triangular conforme mostrado na figura a seguir:

números combinatórios do triângulo de Tartaglia ou Pascal

Por exemplo, o número combinatório

$\displaystyle \begin{pmatrix} 4 \\ 2 \end{pmatrix}$

retorna 6, porque no triângulo de Tartaglia há um 6.

Portanto, se você souber construir o triângulo de Tartaglia ou de Pascal, poderá calcular qualquer número combinatório rapidamente e sem usar sua fórmula.

Binômio de Newton

Outro uso do triângulo de Tartaglia (ou Pascal) é poder calcular potências de binômios (clique neste link para saber o que é um binômio).

Um exemplo de potencialização de um binômio são identidades notáveis, como:

$(a+b)^2$

Identidades notáveis são muito importantes para a matemática, porque nos permitem salvar muitos cálculos e resolver operações complicadas de forma direta e rápida. É por isso que recomendamos verificar o link a seguir se você ainda não sabe o que são Identidades Notáveis .

Como você viu no link anterior, produtos notáveis podem ser resolvidos diretamente com suas fórmulas. Mas… o que acontece quando o par é elevado ao cubo ou a um grau superior?

$\begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}$

Pois bem, esses binômios podem ser calculados de uma forma muito simples com o triângulo de Tartaglia graças ao teorema binomial (ou binômio de Newton). uma vez que embora domine o método, ele é rápido de aplicar, para explicá-lo bem é necessária uma página inteira. Então se você está mais interessado em como resolver esse tipo de binômio, clique na página vinculada e veja como isso é feito.

Combinatória

O triângulo de Tartaglia, ou triângulo de Pascal, também pode ser usado para determinar combinações e probabilidades.

Se alguma vez nos depararmos com um problema em que precisamos de determinar quantos grupos diferentes podem ser formados a partir de um grupo, independentemente da ordem, podemos utilizar o triângulo de Tartaglia.

Por exemplo, se tivermos 5 cartas, para saber de quantas maneiras podemos escolher 3, basta ir à terceira coluna (a primeira coluna é zero) da quinta linha (a primeira linha também é a linha 0) do triângulo de Tartaglia. O número nesta posição (10) corresponde ao número de possibilidades que existem para escolher 3 cartas.

$1 \quad 5 \quad 10 \quad \color{blue}\boxed{ \color{black}10} \color{black} \quad 5 \quad 1$

Assim, a partir de 5 cartas, podem ser formados 10 grupos diferentes de três cartas.

Propriedades do triângulo Tartaglia ou Pascal

O triângulo de Tartaglia, também chamado de triângulo de Pascal, possui as seguintes características:

O triângulo de Tartaglia (ou Pascal) é simétrico, ou seja, a linha vertical que divide todo o triângulo em dois triângulos equiláteros iguais é um eixo de simetria.

A soma horizontal de todos os números em qualquer linha do triângulo de Pascal é igual a uma potência de 2.

propriedades do triângulo de tartaglia ou pascal

As diagonais do triângulo de Tartaglia também são importantes: os números da primeira diagonal (diagonal externa) são uns, a segunda diagonal é formada pela sequência de todos os números naturais, a terceira diagonal corresponde aos números triangulares e a quarta diagonal é composta de números tetragonais (ou tetraédricos).

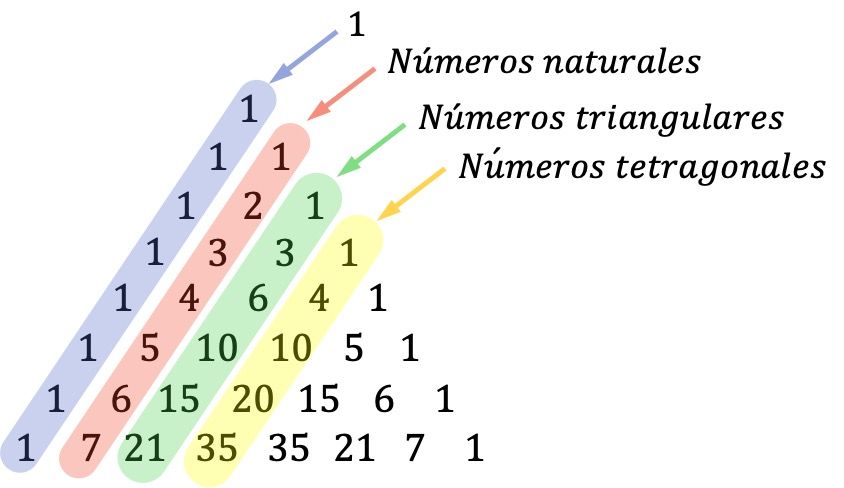
triângulo tartaglia ou números triangulares e tetragonais pascal

Números triangulares são números que podem ser representados na forma de um triângulo. E os números tetragonais são aqueles que formam pirâmides triangulares.

Se você não sabe o que são números triangulares ou tetragonais, nada acontece, é apenas uma curiosidade sobre o triângulo de Tartaglia. Porém, você precisa saber o significado dos números naturais (números usados para contar elementos).

Com exceção do número 1, se o primeiro número de uma linha for um número primo, todos os números dessa mesma linha serão divisíveis por esse número. Por exemplo, na oitava linha (1-7-21-35-35-21-7-1), os números 7, 21 e 35 podem ser divididos por 7 (sete é um número primo).

Outra peculiaridade do triângulo de Tartaglia é que a série de Fibonacci pode ser encontrada somando as diagonais de uma determinada maneira:

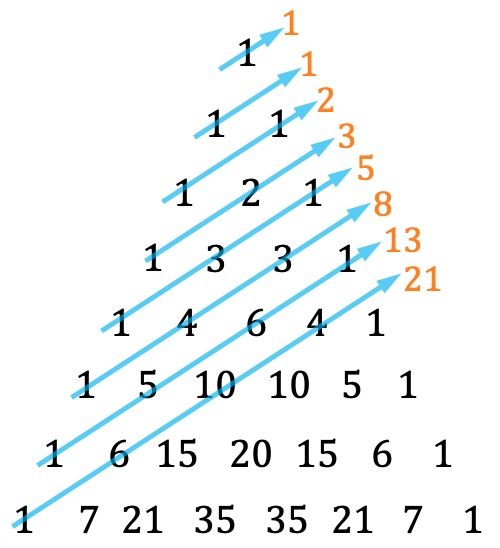
tartaglia ou triângulo pascal série fibonacci

Lembre-se que cada termo da sequência de Fibonacci é igual à soma dos dois anteriores, sendo os dois primeiros termos 1 e 1. Assim, os números que pertencem à sequência de Fibonacci são: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144, 233,…

Se somarmos dois números consecutivos da terceira diagonal do triângulo de Pascal (1-3-6-10-15-…) obtemos um quadrado perfeito (1, 4, 9, 16, 25,…).

Se pintarmos os números pares do triângulo de Pascal com uma cor e os números ímpares com outra cor, obtemos a figura do triângulo de Sierpinski, famoso conjunto geométrico. Abaixo você pode ver o triângulo de Pascal com altura de 512 representado com os números ímpares coloridos em preto e os números pares coloridos em branco:

Triângulo de Sierpinski de Tataglia ou Triângulo de Pascal

A conjectura de Singmaster diz que o número de vezes que cada número maior que 1 ocorre é finito. Ou, em outras palavras, embora o número de linhas no triângulo de Tartaglia seja infinito, o número de vezes que cada número aparece, exceto 1, é finito. A título de curiosidade, o número 3003 é o único conhecido até hoje que aparece até oito vezes no triângulo.

História do triângulo Tartaglia ou Pascal

Agora que sabemos como é o triângulo de Tartaglia, vamos ver quando este triângulo matemático muito especial foi inventado.

Embora o nome do triângulo aritmético seja atribuído principalmente aos famosos cientistas Tartaglia e Pascal, este triângulo algébrico já foi utilizado antes.

O primeiro registro de um triângulo formado por coeficientes binomiais data do século X na Índia. Contudo, os persas começaram a estudar as suas propriedades, nomeadamente os matemáticos Al-Karaji (953-1029) e Omar Khayyam (1048-1131). É por isso que no Irã foi popularizado como triângulo Khayyam-Pascal ou mesmo simplesmente triângulo Khayyam .

Este triângulo começou a ser introduzido na China no século XI pelo matemático Jia Xian, mas foi mais tarde no século XIII que Yang Hui o introduziu como o triângulo aritmético . E por isso, no país asiático o chamam de triângulo Yang Hui .

O triângulo matemático chegou ao continente europeu posteriormente através do alemão Petrus Apianus, publicado especificamente no ano de 1527 no seu livro Rechnung . A partir daí, o famoso algebrista italiano Niccolò Fontana Tartaglia estudou a fundo o triângulo durante a primeira metade do século XVI, e em sua homenagem em países como a Itália ele é conhecido como triângulo de Tartaglia.

Finalmente, o francês Blaise Pascal demonstrou muitas das propriedades do triângulo estudado em sua publicação do Tratado sobre o Triângulo Aritmético em 1654, daí o nome triângulo de Pascal. Deve-se notar que algumas destas propriedades já eram conhecidas, mas foi Pascal quem realizou a sua demonstração por indução matemática.

Triângulo de tartaglia (ou pascal)