Nesta página você encontrará a explicação de como é feita a adição de polinômios. Além disso, você poderá ver exemplos de somas de polinômios e até exercícios resolvidos passo a passo. Por fim, explicamos também quais são as propriedades deste tipo de operação com polinômios.
Como adicionar polinômios?
Em matemática, para adicionar dois ou mais polinômios, os termos dos polinômios que são semelhantes devem ser somados. Ou seja, somar polinômios consiste em somar termos que possuem a mesma parte literal (mesmas variáveis e mesmos expoentes).
Assim, uma soma de polinômios pode ser feita de duas maneiras diferentes: com o método vertical ou com o método horizontal. Abaixo está a explicação de ambos os procedimentos, mas aconselhamos que você aprenda primeiro como adicionar polinômios verticalmente e depois passe para o método horizontal. Obviamente fique com o que você preferir.
Adicionando polinômios verticais
A seguir, veremos como dois polinômios são adicionados verticalmente usando um exemplo:
- Adicione os dois polinômios a seguir:
![]()
![]()
A primeira coisa que precisamos fazer é colocar um polinômio abaixo do outro, de modo que os termos semelhantes dos dois polinômios fiquem alinhados por colunas:
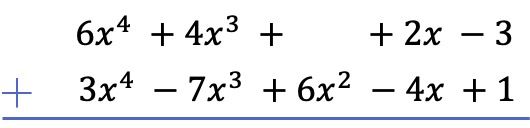
Atenção: Se um polinômio não possuir termo de determinado grau, o espaço deve ser deixado vazio. Por exemplo
![]()
Você não possui um monômio de grau 2, por isso há um espaço vazio em seu site.
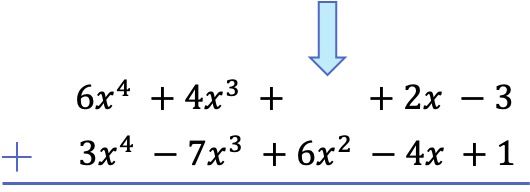
Depois de colocar todos os termos em ordem do grau mais alto para o mais baixo, adicionamos os coeficientes em cada coluna mantendo as partes literais iguais:
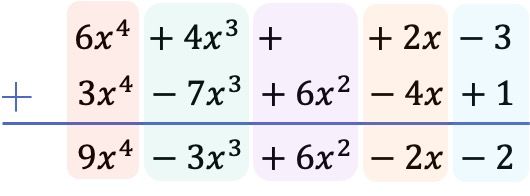
Consequentemente, o resultado obtido da soma dos 2 polinômios é:
![]()
Agora que você entende a adição de polinômios, saiba que também é possível somar frações formadas por polinômios. Este tipo de operação é chamada de adição de frações algébricas . Clique neste link e aprenda não apenas como são calculadas as somas das frações algébricas, mas também como são resolvidas todas as operações com frações algébricas.
Adição horizontal de polinômios
Acabamos de ver como adicionar polinômios verticalmente, mas agora veremos o outro método para adicionar polinômios: adicionar polinômios horizontalmente. Certamente este procedimento é mais rápido que o anterior, porém é necessário ter um domínio maior dos conceitos de polinômios.
Então vamos ver em que consiste esse método de somar polinômios por meio de um exemplo. E para que você possa ver as diferenças entre os dois métodos, adicionaremos os mesmos polinômios do exemplo anterior:
- Calcule a soma dos dois polinômios a seguir:
![]()
![]()
Você deve primeiro posicionar os dois polinômios na mesma operação, ou seja, um após o outro:
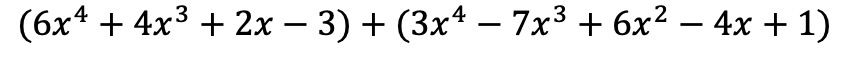
E agora somamos os termos que possuem partes literais idênticas, ou seja, os termos com as mesmas variáveis (letras) e os mesmos expoentes. Termos que não sejam semelhantes não podem ser adicionados.
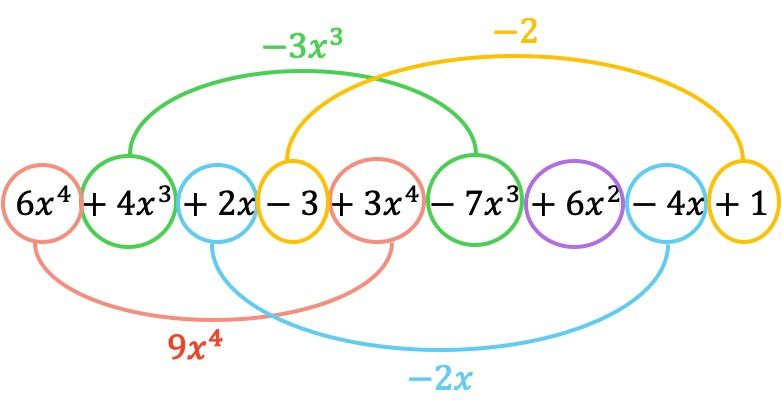
O polinômio resultante da adição é, portanto:

Como você pode ver, obtivemos o mesmo resultado com ambos os métodos, portanto, ao adicionar polinômios você pode usar o que melhor lhe convier.
Problemas resolvidos de adição de polinômios
Para que você possa praticar, deixamos vários exercícios resolvidos de somas de polinômios. Se você tiver alguma dúvida, pode perguntar nos comentários da página e responderemos o mais breve possível.
Exercício 1
Adicione os dois polinômios a seguir:
![]()
![]()
Neste caso, adicionaremos os dois polinômios verticalmente. Para fazer isso, ordenamos os polinômios por grau e somamos os monômios localizados na mesma coluna:
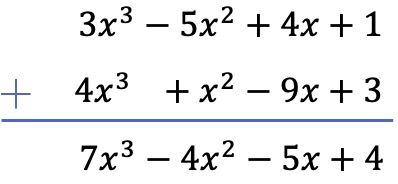
Exercício 2
Resolva a soma dos dois polinômios a seguir:
![]()
![]()
Somaremos os dois polinômios usando o método vertical. Portanto, ordenamos os polinômios por grau e somamos os termos localizados na mesma coluna:
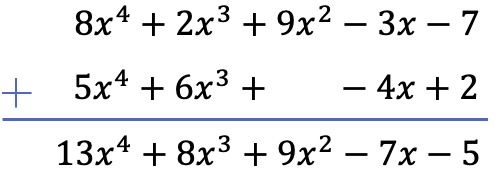
Observe que neste caso particular, deve-se deixar um espaço em branco na coluna de grau 2 do segundo polinômio, pois não possui termo quadrático.
Exercício 3
Qual é a soma dos dois polinômios a seguir?
![]()
![]()
Realizaremos a adição dos dois polinômios usando o método vertical. ENTÃO:
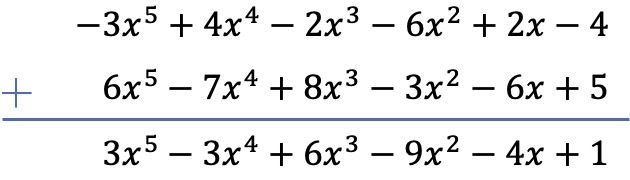
Exercício 4
Calcule a soma dos três polinômios a seguir:
![]()
![]()
![]()
Calcularemos a soma dos 3 polinômios usando o método vertical. Colocamos, portanto, os polinômios ordenados por grau e somamos os termos localizados na mesma coluna:
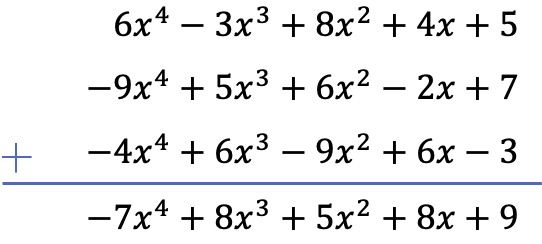
👉👉👉Agora que você viu como dois polinômios se somam, você pode estar interessado em outra operação característica dos polinômios: o fator comum. Extrair um fator comum de um polinômio é bastante complicado (e difícil de entender); na verdade, muitos erros são cometidos ao fazer isso. Por isso preparamos um guia onde explicamos passo a passo como extrair o fator comum , para que você entenda perfeitamente e não cometa erros ao fazer esta operação. Descubra quais são as dicas para extrair o fator comum de um polinômio clicando no link.
Propriedades de adição de polinômios
A soma dos polinômios possui as seguintes características:
- Propriedade associativa : Ao adicionar 3 ou mais polinômios, não importa como os polinômios são agrupados porque o resultado é sempre o mesmo. Ou seja, verifica-se a seguinte igualdade:
![]()
- Propriedade comutativa : na adição de polinômios a ordem das adições não modifica o resultado da adição.
![]()
- Elemento neutro : Obviamente, adicionar um polinômio mais qualquer outro polinômio com valor numérico zero é equivalente ao primeiro polinômio.
![]()
- Elemento oposto : O resultado da adição de qualquer polinômio mais seu polinômio oposto é sempre zero.
![]()
O que você acha da explicação? Você achou isso útil? Qual método de adição de polinômios você prefere, vertical ou horizontal? Nós lemos você nos comentários! 👀