Sistemas de equações são conjuntos de duas ou mais equações que possuem mais de uma incógnita. Assim, para resolver sistemas, podemos utilizar quatro métodos: substituição, equalização, redução e representação gráfica. Mas, antes de começarmos a explicar os procedimentos de solução, definiremos os tipos de sistemas que existem de acordo com o número de soluções:
- Sistema compatível determinado: possui apenas uma solução e pode ser representado por duas retas que se cruzam em um único ponto (que é a solução).
- Sistema compatível indeterminado: possui infinitas soluções e isso se deve ao fato de existirem duas retas que coincidem nos mesmos pontos.
- Sistema incompatível: não tem solução, pois as retas são paralelas e portanto não possuem ponto em comum.
Métodos para resolver sistemas de equações lineares
Explicaremos agora os diferentes sistemas que podemos usar para resolver sistemas de equações. Nas explicações você encontrará a teoria e alguns exemplos, graças aos quais todos os conceitos explicados ficarão mais claros. Observe que neste artigo falaremos apenas de sistemas de equações 2×2 , o que significa que trataremos simplesmente de sistemas compostos por duas equações. Dito isto, vamos começar com a explicação.
método de substituição
O método de substituição consiste em isolar uma das incógnitas de uma das equações e depois substituir a expressão obtida na equação oposta. Este método é mais recomendado quando pelo menos uma das incógnitas tem o valor do coeficiente igual a 1. Assim, os passos a seguir são muito simples:
- Isole uma quantidade desconhecida de uma das duas equações.
- Substitua na outra equação a expressão equivalente à incógnita que eliminamos da primeira equação.
- Apague a incógnita oposta na equação que obtivemos.
- Assim que tivermos o valor da primeira variável, precisamos usá-lo para encontrar a segunda.
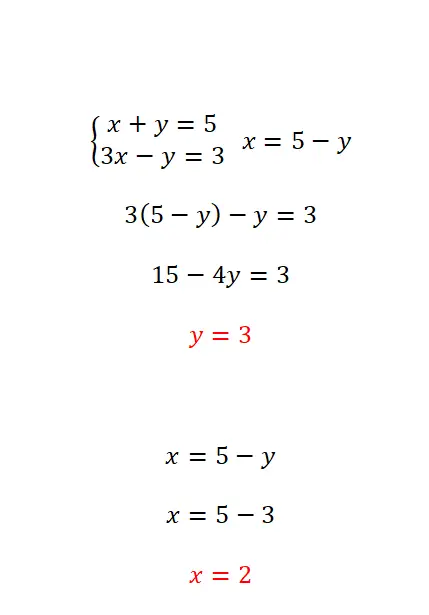
método de equalização
O método de emparelhamento consiste em isolar a mesma variável nas duas equações e depois combinar as duas expressões obtidas. Este método é recomendado quando a mesma incógnita pode ser facilmente isolada em ambas as equações, pois facilita todo o cálculo. O procedimento que você deve seguir neste caso é o seguinte:
- Isolamos a incógnita que escolhemos nas duas equações.
- Assimilamos as expressões equivalentes a esta incógnita.
- Resolvemos a equação normalmente.
- Calculamos a outra incógnita com o valor que calculamos.
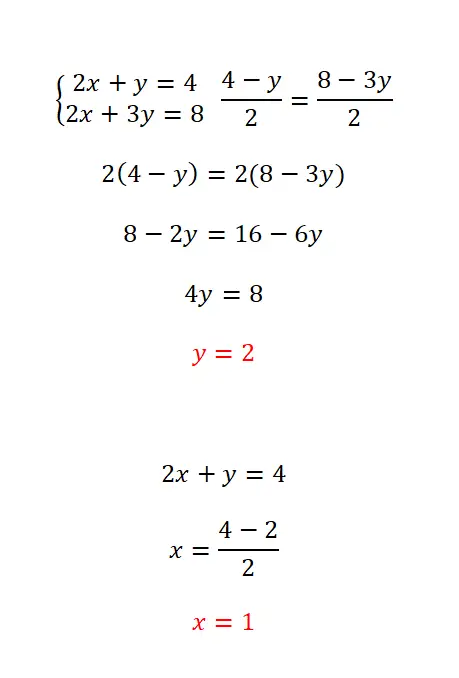
método de redução
O método de redução baseia-se na multiplicação de ambas as equações por dois números, o que nos permite obter o mesmo coeficiente com sinal diferente de uma das variáveis em ambas as expressões. Este método é mais recomendado quando uma mesma incógnita possui o mesmo coeficiente em todas as equações ou no caso de possuir os mesmos coeficientes de sinais opostos. E o procedimento de resolução é o seguinte:
- As duas equações são multiplicadas pelos números necessários (é necessário encontrar dois números que permitam obter o mesmo coeficiente para uma das duas variáveis das duas equações, mas de sinal oposto).
- Em seguida, as equações são subtraídas ou somadas para eliminar essa incógnita com seus respectivos coeficientes.
- Então a equação restante é resolvida.
- E utilizamos o resultado desta equação para obter o valor numérico que falta na outra variável.
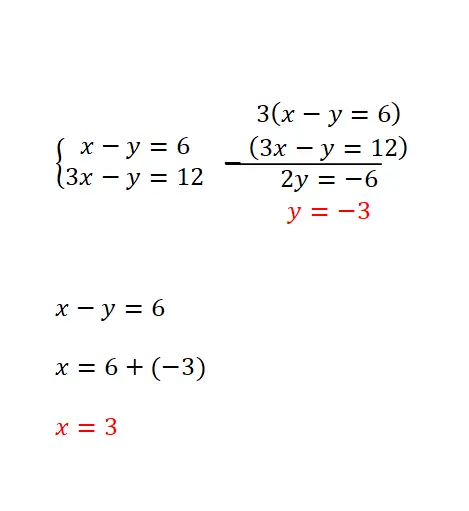
método gráfico
Finalmente, podemos optar por resolver um sistema de equações por meio de uma representação gráfica . Este método é bem diferente dos demais, pois não possui uma parte matemática complexa, é quase inteiramente gráfico. Assim, para saber os valores das incógnitas, devemos estruturar as duas equações na forma da equação da reta: y = mx + b . Desta forma poderemos fazer a representação então, associaremos os valores das coordenadas do ponto de corte entre as duas funções com as incógnitas. Aqui está um exemplo prático:
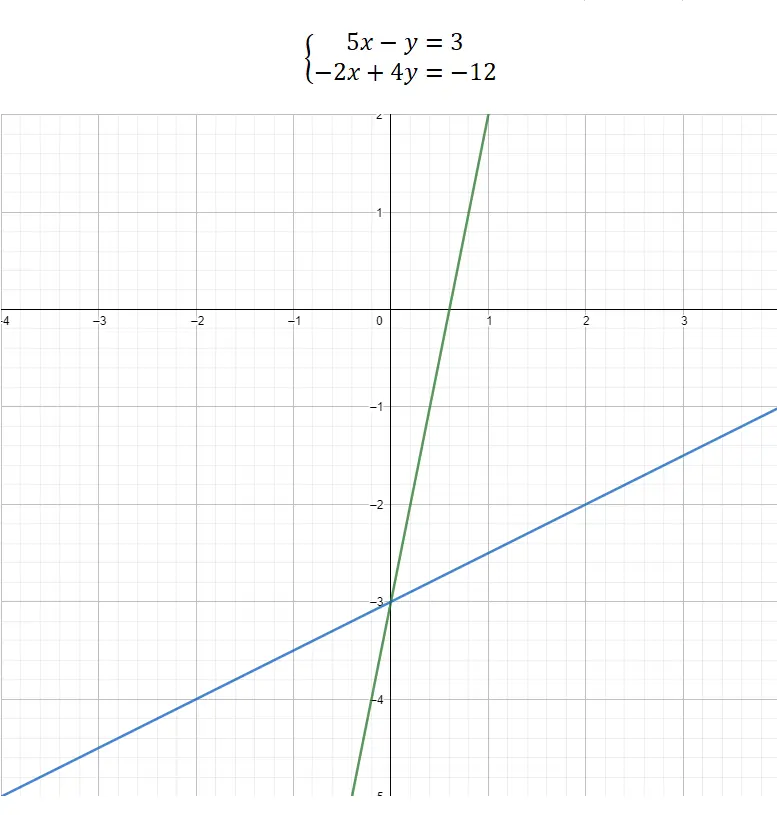
Como pode ser visto no gráfico, o ponto de corte entre as duas funções é (0, -3). Portanto, o valor de x = 0 e o valor de y = -3. É assim que um sistema de equações é resolvido graficamente.
Como resolver um sistema de equações quadráticas?
Para resolver sistemas de equações quadráticas, podemos utilizar os métodos que acabamos de discutir. Pessoalmente, gostamos de recomendar o método de substituição porque nos permite obter rapidamente uma equação com uma única incógnita. Por outro lado, se utilizarmos os métodos de redução ou equalização, o cálculo torna-se bastante complicado. Assim, depois de substituir uma das duas variáveis, você só precisa resolver a equação quadrática ou equação quadrática resultante. Aqui está um exemplo para que você possa ver todo o processo:
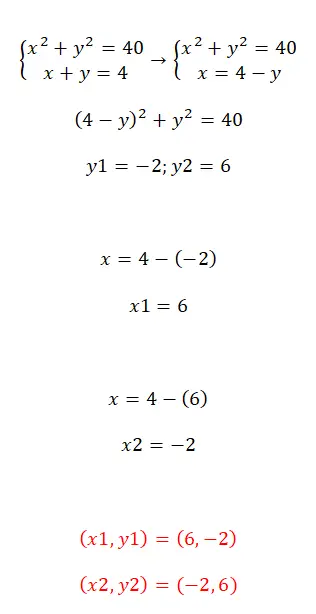
Exercícios de resolução de sistemas de equações
Oferecemos agora alguns exercícios sobre sistemas de equações lineares e quadráticas para que você possa aplicar a teoria explicada. Desta forma você entenderá melhor todos os conceitos relacionados ao cálculo de sistemas de equações. Recomendamos que você tente resolvê-los antes de olhar as respostas que oferecemos, assim você aproveitará ao máximo os exercícios:
Exercício 1
Resolva este sistema de equações usando o método de substituição:
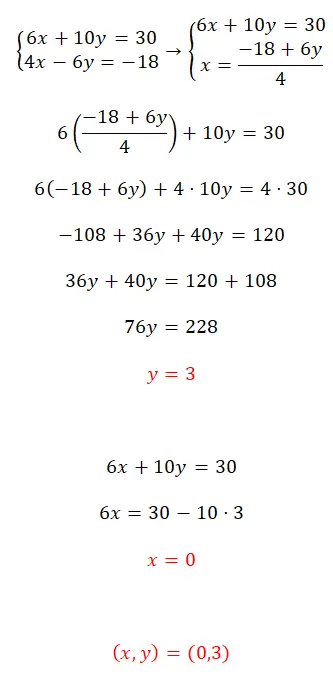
- Começamos isolando uma das duas incógnitas em uma equação.
- A seguir substituímos a expressão obtida na equação oposta, pela incógnita que resolvemos anteriormente.
- Obtemos então o resultado da variável oposta.
- A seguir, substituímos o primeiro valor descoberto em uma das duas equações para calcular o valor da primeira incógnita.
- Por fim, expressamos o resultado das duas variáveis.
Exercício 2
Resolva este sistema de equações usando o método de substituição:
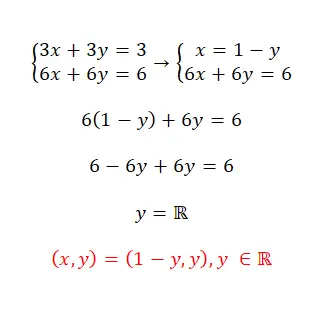
- Neste caso seguiremos o mesmo procedimento: isolar uma incógnita, substituí-la na outra expressão e isolar a segunda variável.
- Como podemos ver, este é um sistema compatível indeterminado, pois possui infinitas soluções.
Exercício 3
Resolva este sistema de equações usando o método de equalização:
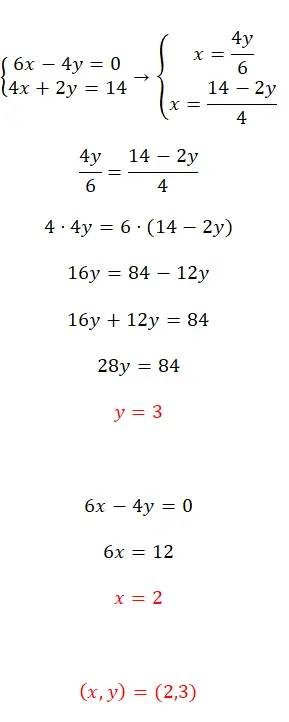
- O primeiro passo é isolar a mesma variável em ambas as equações, neste caso escolhemos x.
- Em seguida, combinamos as expressões resultantes e começamos a resolver.
- Assim, obtemos o valor da primeira incógnita.
- E se a substituirmos numa das duas equações originais, podemos calcular a segunda incógnita.
- Por fim, expressamos o resultado das duas variáveis.
Exercício 4
Resolva este sistema de equações usando o método de equalização:
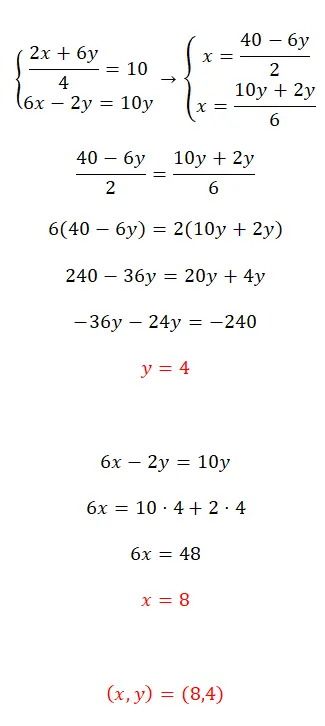
- Primeiro, isolamos o x em ambas as equações.
- A seguir, combinamos as expressões que obtivemos.
- Obtemos o valor da primeira incógnita.
- Substituímos esse valor em uma das duas equações iniciais e calculamos a segunda incógnita.
- Finalmente, expressamos o valor dos dois estranhos.
Exercício 5
Resolva este sistema de equações usando o método de redução:
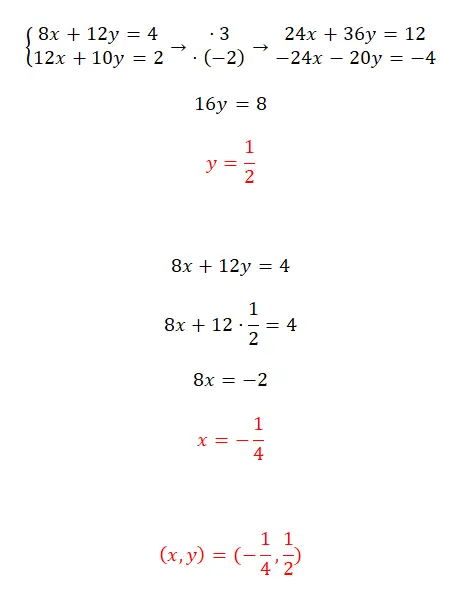
- É necessário procurar dois números que permitam obter o mesmo coeficiente para uma das duas variáveis das duas equações, mas de sinal oposto .
- Depois, basta resolver a equação que obtemos somando as duas expressões obtidas.
- A seguir, substituímos y em uma das duas equações originais, para calcular x.
- Finalmente, expressamos o resultado do sistema.
Exercício 6
Resolva este sistema de equações usando o método de redução:
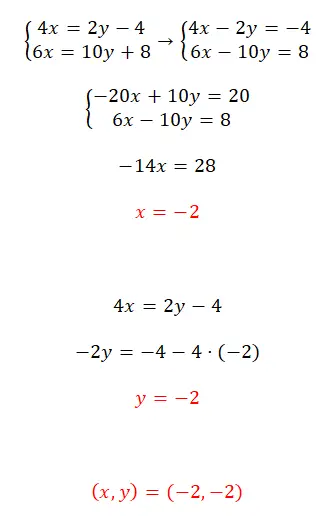
- Começamos organizando as equações (passando todas as variáveis para a esquerda).
- Então multiplicamos a primeira equação por -5.
- Resolvemos a equação que obtemos somando as duas equações e obtemos o valor de x.
- Usamos esse valor conhecido para obter o valor de y.
- Expressamos o resultado do sistema de equações.
Exercício 7
Resolva este sistema de equações usando o método de substituição:
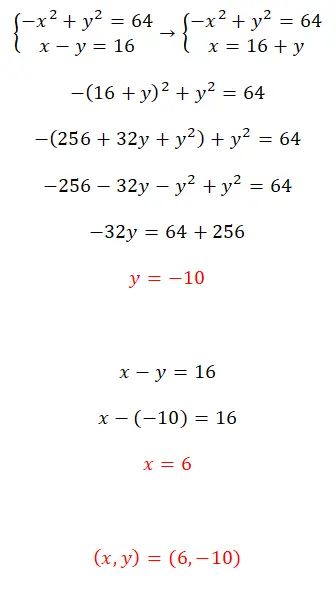
- Para resolver este sistema de equações não lineares, recomendamos o uso do método de substituição.
- Então você constrói uma equação com a expressão equivalente a x.
- Você obtém o valor do desconhecido y.
- Você calcula o valor de x com o valor calculado anteriormente.
- E você já tem os dois valores.
Exercício 8
Resolva este sistema de equações usando o método de sua escolha:
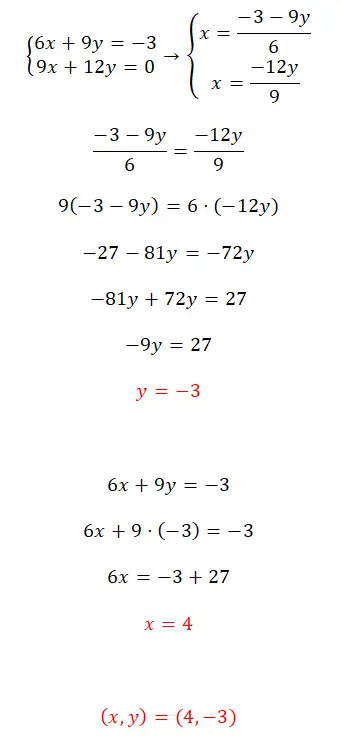
- Neste caso, nos é apresentado um determinado sistema compatível e iremos resolvê-lo utilizando o método de equalização.
- Portanto, resolvemos x em ambas as equações e igualamos as duas expressões resultantes.
- Depois de resolver a equação, obtemos o valor de y.
- Usamos esse valor para encontrar o valor de x.
- Finalmente, expressamos o resultado do sistema.