Seções cônicas - Mathority

Nesta página você encontrará a definição de seções cônicas, porque elas são tão importantes e os diferentes tipos de seções cônicas que existem (círculo, elipse, hipérbole e parábola). Além disso, você poderá ver as diferenças entre suas equações.

O que são seções cônicas?

Na geometria analítica, secções cónicas (ou simplesmente cónicas) são todas as curvas resultantes das diferentes intersecções entre um cone e um plano, quando este plano não passa pelo vértice do cone. Existem quatro tipos de seções cônicas: o círculo, a elipse, a parábola e a hipérbole.

Abaixo estão as 4 seções possíveis que podem ser obtidas de qualquer cone:

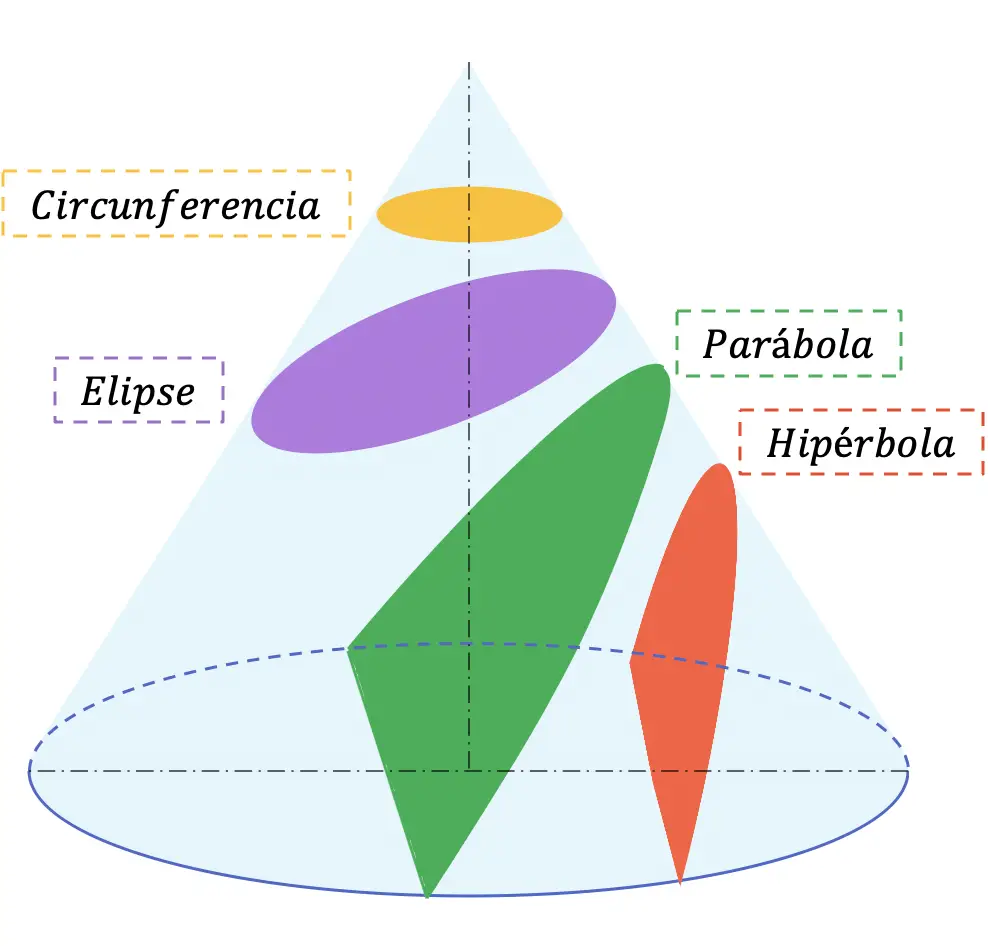
As seções cônicas são geralmente estudadas no ensino médio (Bachillerato), nas disciplinas de matemática e desenho técnico.

Tipos de seções cônicas

Depois de vermos o conceito de seção cônica, vamos ver quais são os quatro tipos de seções cônicas que existem: o círculo, a elipse, a parábola e a hipérbole.

circunferência

A circunferência é uma seção cônica que pode ser encontrada cortando um cone com um plano perpendicular ao seu eixo de revolução (paralelo à base).

Além disso, a circunferência é o lugar geométrico dos pontos do plano equidistantes de um ponto fixo denominado centro.

Elipse

A elipse é uma linha plana, fechada e curva muito semelhante à circunferência, mas seu formato é mais oval. Em particular, resulta do corte da superfície de um cone por um plano oblíquo cujo ângulo em relação ao eixo de revolução é maior que o do gerador.

Além disso, todos os pontos de uma elipse satisfazem uma condição: a elipse é o lugar geométrico de todos os pontos de um plano cuja soma das distâncias a dois outros pontos fixos (chamados focos F e F’) é constante.

Parábola

Em matemática, uma parábola é o lugar geométrico dos pontos no plano que são equidistantes de um ponto fixo (chamado de foco) e de uma linha fixa (chamada de diretriz).

Geometricamente, a parábola é o resultado da seção de um cone por um plano com ângulo de inclinação em relação ao eixo de revolução equivalente ao ângulo da geratriz do cone. Portanto, o plano que contém a parábola é paralelo ao gerador do cone.

Uma característica muito importante desta seção cônica é a equação da parábola , pois dependendo do seu estado permite identificar que tipo de parábola se trata. Neste link você encontrará todas as equações da parábola, quais são os elementos da parábola, suas propriedades, exemplos, exercícios resolvidos,… entre outras características das parábolas.

Hipérbole

Por ser uma seção cônica, uma hipérbole é obtida quando um cone é cortado por um plano com ângulo menor que o ângulo formado pelo gerador do cone em relação ao seu eixo de revolução.

Matematicamente, uma hipérbole pode ser definida como o lugar geométrico dos pontos do plano que satisfazem a seguinte propriedade: o valor absoluto da diferença nas distâncias entre qualquer ponto da hipérbole e dois pontos fixos (chamados focos) deve ser constante.

Além disso, o valor da subtração destas duas distâncias é sempre equivalente à distância entre os dois vértices da hipérbole.

$\lvert d_1 - d_2 \rvert = 2a$

Como tenho certeza que você já deduziu, o valor do parâmetro

$a$

de uma hipérbole é fundamental para hipérboles. No link a seguir você poderá ver nossa explicação sobre a hipérbole, onde descobrirá porque é um coeficiente tão importante e também quais são todos os elementos que caracterizam uma hipérbole. Além disso, você encontrará a aparência da equação de uma hipérbole , os diferentes tipos de hipérboles que existem e até mesmo problemas e exercícios passo a passo sobre hipérboles.

Equação geral de seções cônicas

Cada seção cônica pode ser expressa analiticamente como uma equação. Na verdade, todas as equações cônicas devem ser de segundo grau:

$Ax^2+Bxy+Cy^2+Dx+Ey+F = 0$

Consequentemente, pelo menos um dos coeficientes

$A, B$

qualquer

$C$

da fórmula deve ser diferente de zero.

Assim, dependendo dos valores dos parâmetros, a equação corresponderá a um tipo ou outro de cônica:

Circunferência : para a equação geral que descreve uma circunferência, os termos
$A$

E

$C$

deve corresponder e

$B$

deve ser zero.

$A=C \qquad B=0$

Elipse : A equação corresponderá à expressão matemática de uma elipse quando verificada a seguinte condição:

$B^2-4AC <0$

Parábola : Para que a equação seja uma parábola, a seguinte igualdade deve ser satisfeita:

$B^2-4AC=0$

Hipérbole : Finalmente, a equação geral de uma hipérbole deve satisfazer a seguinte desigualdade:

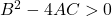$B^2-4AC>0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”112″ style=”vertical-align: -2px;”></p></p> </div> </div> </article> <nav class=$ Navegação de Post

← Post anterior

Post seguinte →