Representação de funções -

Neste artigo veremos como representar qualquer tipo de função em um gráfico. Além disso, você encontrará exercícios passo a passo resolvidos sobre a representação de funções em um gráfico.

Como representar uma função em um gráfico

Para representar uma função em um gráfico, as seguintes etapas devem ser executadas:

Encontre o domínio da função.
Calcule os pontos de corte da função com os eixos cartesianos.
Calcule as assíntotas da função.
Estude a monotonicidade da função e encontre seus extremos relativos .
Estude a curvatura da função e encontre seus pontos de inflexão .
Trace os pontos de corte, assíntotas, extremos relativos e pontos de inflexão e, em seguida, represente graficamente a função.

Exemplo de representação de uma função

Para que você possa ver como uma função é representada graficamente, resolveremos passo a passo o seguinte exercício:

Trace a seguinte função racional em um gráfico:

$f(x)=\cfrac{x^2}{x-1}$

A primeira coisa a fazer é calcular o domínio da função . Esta é uma função racional, então precisamos igualar o denominador a zero para ver quais números não pertencem ao domínio da função:

$x-1=0$

$x=1$

Então, quando x for 1, o denominador será 0 e portanto a função não existirá. O domínio da função, portanto, consiste em todos os números reais, exceto x=1.

$\text{Dom } f= \mathbb{R}-\{1 \}$

Para encontrar o ponto de intersecção com o eixo X , devemos resolver a equação

$f(x)= 0.$

Como a função sempre tem valor 0 no eixo X:

$f(x)=0$

$\cfrac{x^2}{x-1} = 0$

O termo

$x -1$

Isso envolve dividir todo o lado esquerdo, para que possamos multiplicá-lo por todo o lado direito:

$x^2 = 0 \cdot (x-1)$

$x^2 = 0$

$x = 0$

O ponto de intersecção com o eixo OX é portanto:

$\bm{(0,0)}$

E para encontrar o ponto de intersecção com o eixo Y , calculamos

$f(0).$

Como x é sempre 0 no eixo Y:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0$

Portanto, o ponto de corte com o eixo OY é:

$\bm{(0,0)}$

Neste caso, quando a função passa pela origem da coordenada, o ponto de intersecção com o eixo X coincide com o ponto de intersecção com o eixo Y.

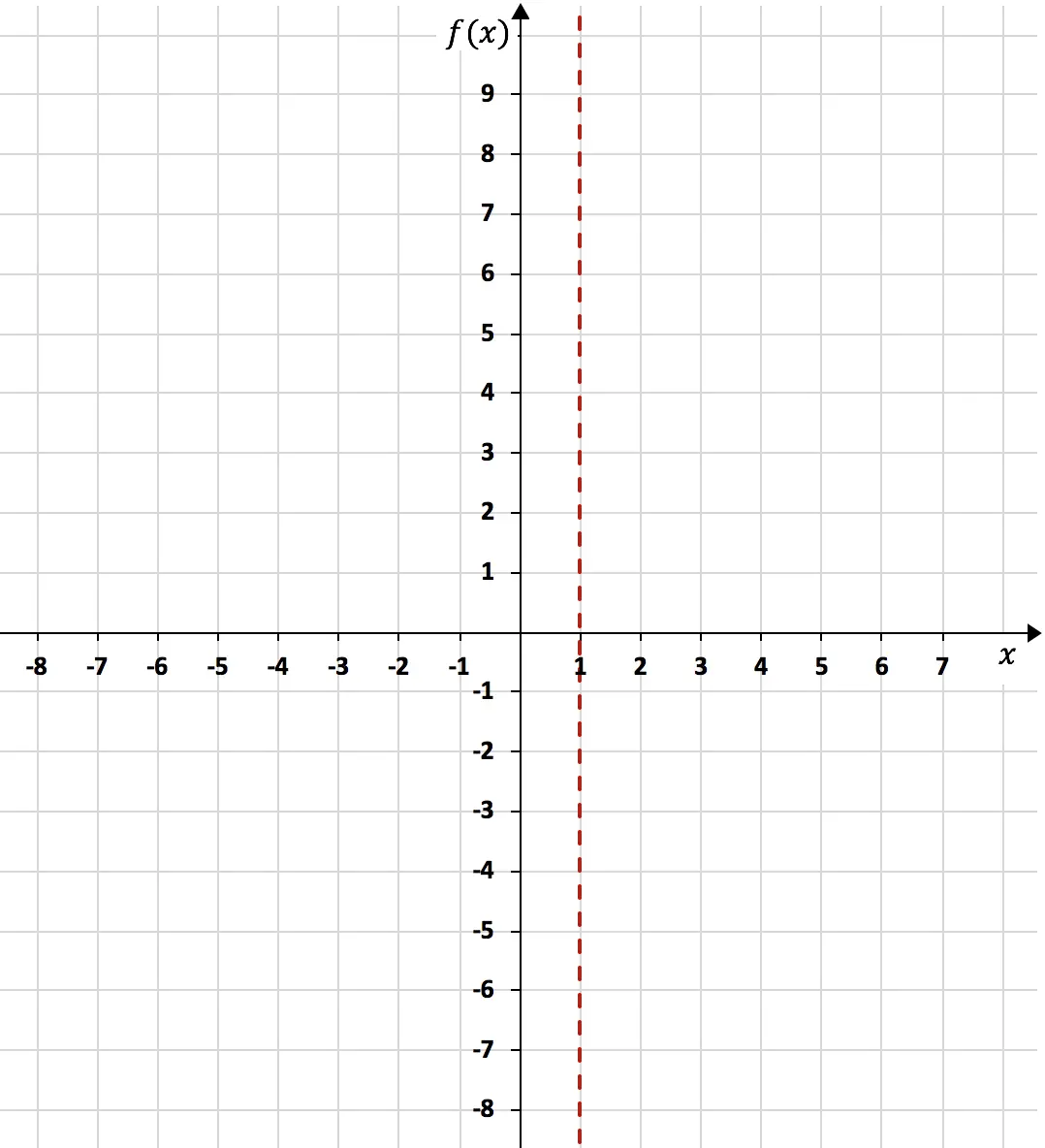
Depois de conhecermos o domínio e os pontos de corte, precisamos calcular as assíntotas da função .

Para ver se a função possui assíntotas verticais, precisamos calcular o limite da função em pontos que não pertencem ao domínio (neste caso x=1). E se o resultado for infinito, é uma assíntota vertical. Ainda:

$\displaystyle \lim_{x \to 1} \ \cfrac{x^2}{x-1} = \cfrac{1^2}{1-1} = \cfrac{1}{0} = \infty$

Como o limite da função quando x tende a 1 dá infinito, x=1 é uma assíntota vertical:

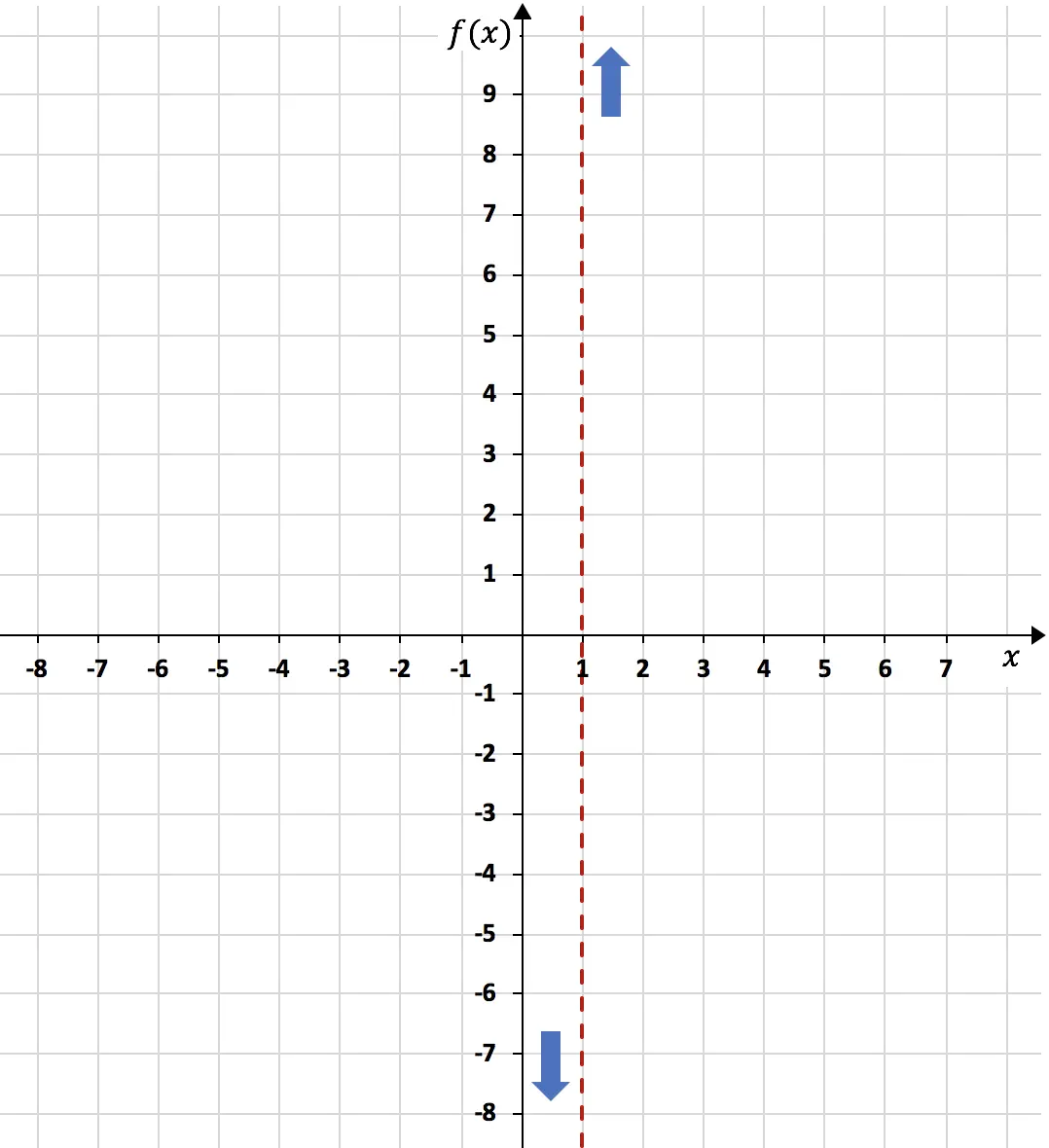
Uma vez calculada a assíntota vertical, é necessário calcular os limites laterais da função em relação a ela. Como não sabemos se a função tenderá a -∞ ou +∞ à medida que se aproxima de x=1 pela esquerda, e não sabemos quando se aproxima de x=1 pela direita.

Assim, procedemos ao cálculo do limite lateral esquerdo da função em x=1:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1}$

Para calcular numericamente um limite lateral em um ponto, devemos substituir um número na função que esteja muito próximo do ponto. Nesse caso, queremos um número bem próximo de 1 à esquerda, como 0,9. Portanto, substituímos o ponto 0,9 na função:

$\cfrac{0,9^2}{0,9-1}=\cfrac{0,81}{-0,1}=-81$

Os limites laterais de uma assíntota só podem fornecer +∞ ou -∞. E como substituindo um número muito próximo de 1 à esquerda na função obtivemos um resultado negativo, o limite à esquerda é -∞:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1} = \bm{-\infty}$

Agora fazemos o mesmo procedimento com o limite do lado direito:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1}$

Substituímos um número muito próximo de 1 à direita na função. Por exemplo, ponto 1.1:

$\cfrac{1,1^2}{1,1-1}=\cfrac{1,21}{0,1}=+12,1$

Neste caso, o resultado do limite lateral é um número positivo. O limite à direita é, portanto, +∞:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1} = \bm{+\infty}$

Concluindo, em x = 1 a função tende para menos infinito à esquerda e mais infinito à direita:

Por outro lado, a assíntota horizontal da função será o resultado do limite infinito da função. Ainda:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2}{x-1} = \cfrac{+\infty}{+\infty } =+\infty$

Lembre-se de como calcular os limites infinitos de funções racionais:

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> </div> O limite infinito da função nos deu +∞, então a função não tem assíntota horizontal. Agora calculamos a assíntota oblíqua. As assíntotas oblíquas têm a forma <p class=$ $y=mx+n$

. E

$m$

É calculado com a seguinte fórmula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:x$

O x é como se tivesse 1 como denominador:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:\cfrac{x}{1}$

É uma divisão de frações, então multiplicamos elas transversalmente:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 \cdot 1 }{(x-1) \cdot x}$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x}$

E calculamos o limite:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x} = \cfrac{+\infty}{+\infty } = \cfrac{1}{1} = 1$

Então m = 1. Agora calculamos

$n$

com a seguinte fórmula:

$\displaystyle n = \lim_{x \to +\infty} \bigl[f(x)-mx\bigr]$

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty$

Mas obtemos a indeterminação infinito menos infinito, então temos que reduzir os termos a um denominador comum. Para fazer isso, multiplicamos e dividimos o termo x pelo denominador da fração:

$\displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]$

Agora que os dois termos têm o mesmo denominador, podemos agrupá-los:

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]$

E finalmente resolvemos o limite:

$\displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1$

Portanto, n = 1. A assíntota oblíqua é, portanto:

$y = mx+n$

$y = 1x+1$

$\bm{y = x+1}$

Uma vez calculada a assíntota oblíqua, representamo-la no mesmo gráfico fazendo uma tabela de valores:

$y=x+1$

$\begin{array}{c|c} x & y \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}$

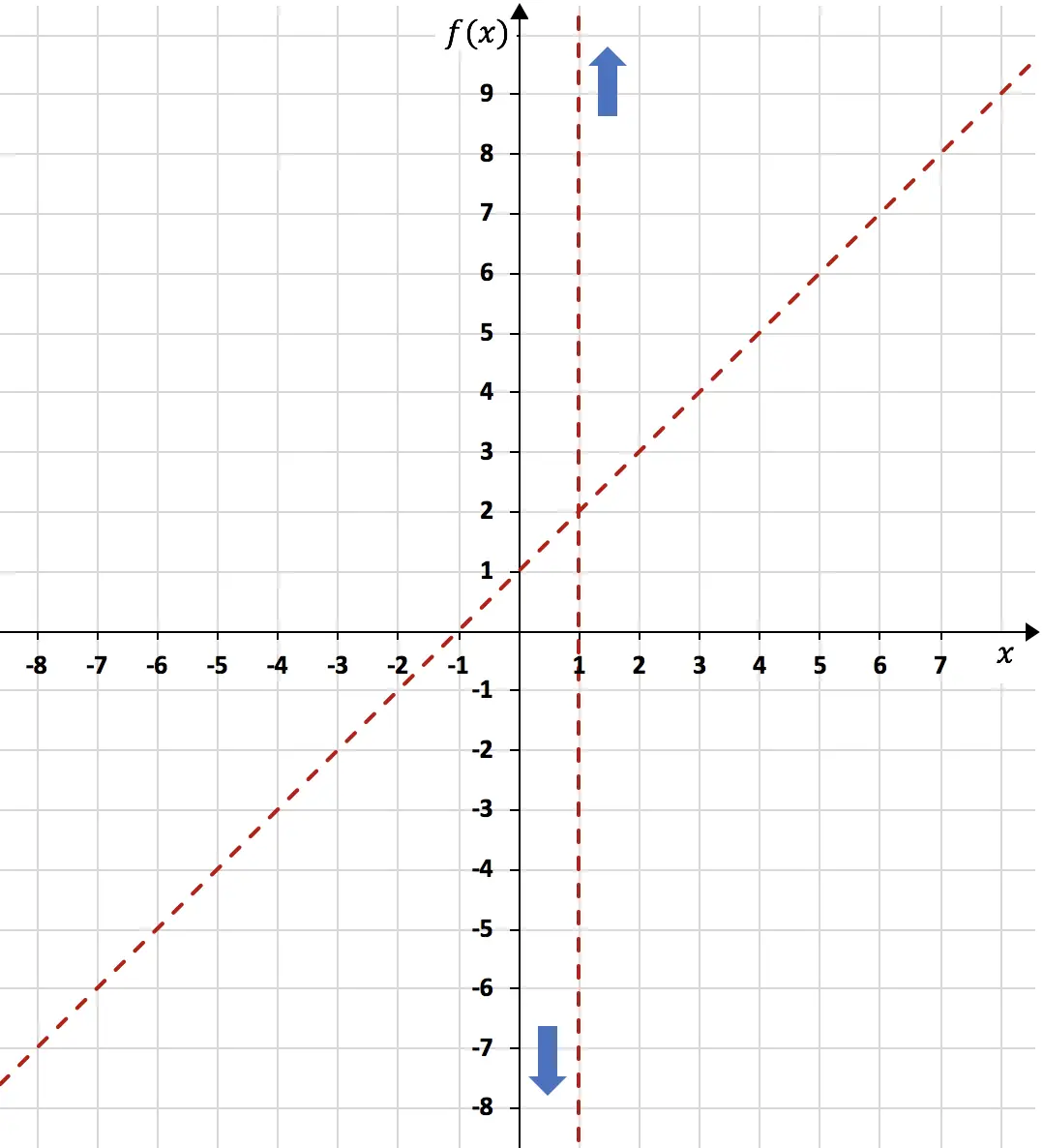
Agora que conhecemos todas as assíntotas da função, precisamos analisar a monotonicidade da função . Ou seja, precisamos estudar em quais intervalos a função aumenta e em quais intervalos ela diminui. Portanto, calculamos a primeira derivada da função:

$f(x)=\cfrac{x^2}{x-1} \ \longrightarrow \ f'(x)= \cfrac{2x\cdot (x-1) - x^2 \cdot 1}{(x-1)^2}$

$f'(x)= \cfrac{2x^2-2x - x^2}{(x-1)^2} = \cfrac{x^2-2x}{(x-1)^2}$

E agora definimos a derivada igual a 0 e resolvemos a equação:

$f'(x)=0$

$\cfrac{x^2-2x}{(x-1)^2}=0$

O termo

$\left(x-1\right)^2}$

Isso envolve dividir todo o lado esquerdo, para que possamos multiplicá-lo por todo o lado direito:

$x^2-2x=0\cdot \left(x-1\right)^2$

$x^2-2x=0$

Extraímos o fator comum para resolver a equação quadrática:

$x(x-2)=0$

Para que a multiplicação seja igual a 0, um dos dois elementos da multiplicação deve ser zero. Portanto, definimos cada fator igual a 0 e obtemos ambas as soluções da equação:

$\displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}$

Representamos agora na reta numérica todos os pontos críticos encontrados, ou seja, os pontos que não pertencem ao domínio (x=1) e aqueles que cancelam a derivada (x=0 e x=2):

E avaliamos o sinal da derivada em cada intervalo, para saber se a função aumenta ou diminui. Portanto, pegamos um ponto em cada intervalo (nunca os pontos críticos) e observamos qual sinal a derivada tem nesse ponto:

$f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}$

$f'(-1) = \cfrac{(-1)^2-2(-1)}{\left((-1)-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

$f'(0,5) = \cfrac{0,5^2-2\cdot 0,5}{\left(0,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(1,5) = \cfrac{1,5^2-2\cdot 1,5}{\left(1,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(3) = \cfrac{3^2-2\cdot 3}{\left(3-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

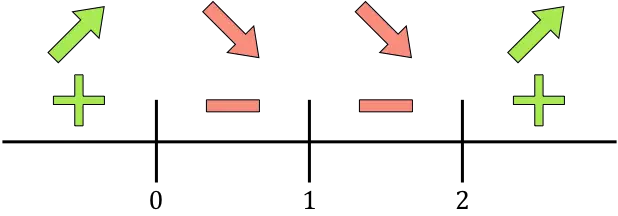
Se a derivada for positiva, significa que a função está aumentando, e se a derivada for negativa, significa que a função está diminuindo. Portanto, os intervalos de crescimento e declínio são:

Crescimento:

$\bm{(-\infty, 0)\cup (2,+\infty)}$

Diminuir:

$\bm{(0,1)\cup (1,2)}$

Além disso, em x=0 a função vai de crescente para decrescente, então x=0 é um máximo relativo da função. E em x=2, a função vai de decrescente para crescente, então x=2 é um mínimo relativo da função.

Finalmente, substituímos os extremos encontrados na função original para encontrar a coordenada Y dos pontos:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0 \ \longrightarrow \ (0,0)$

$f(2)=\cfrac{2^2}{2-1} = \cfrac{4}{1} = 4 \ \longrightarrow \ (2,4)$

Os extremos relativos da função são, portanto:

Máximo no ponto

$\bm{(0,0)}$

Mínimo para apontar

$\bm{(2,4)}$

Representamos o máximo e o mínimo no gráfico:

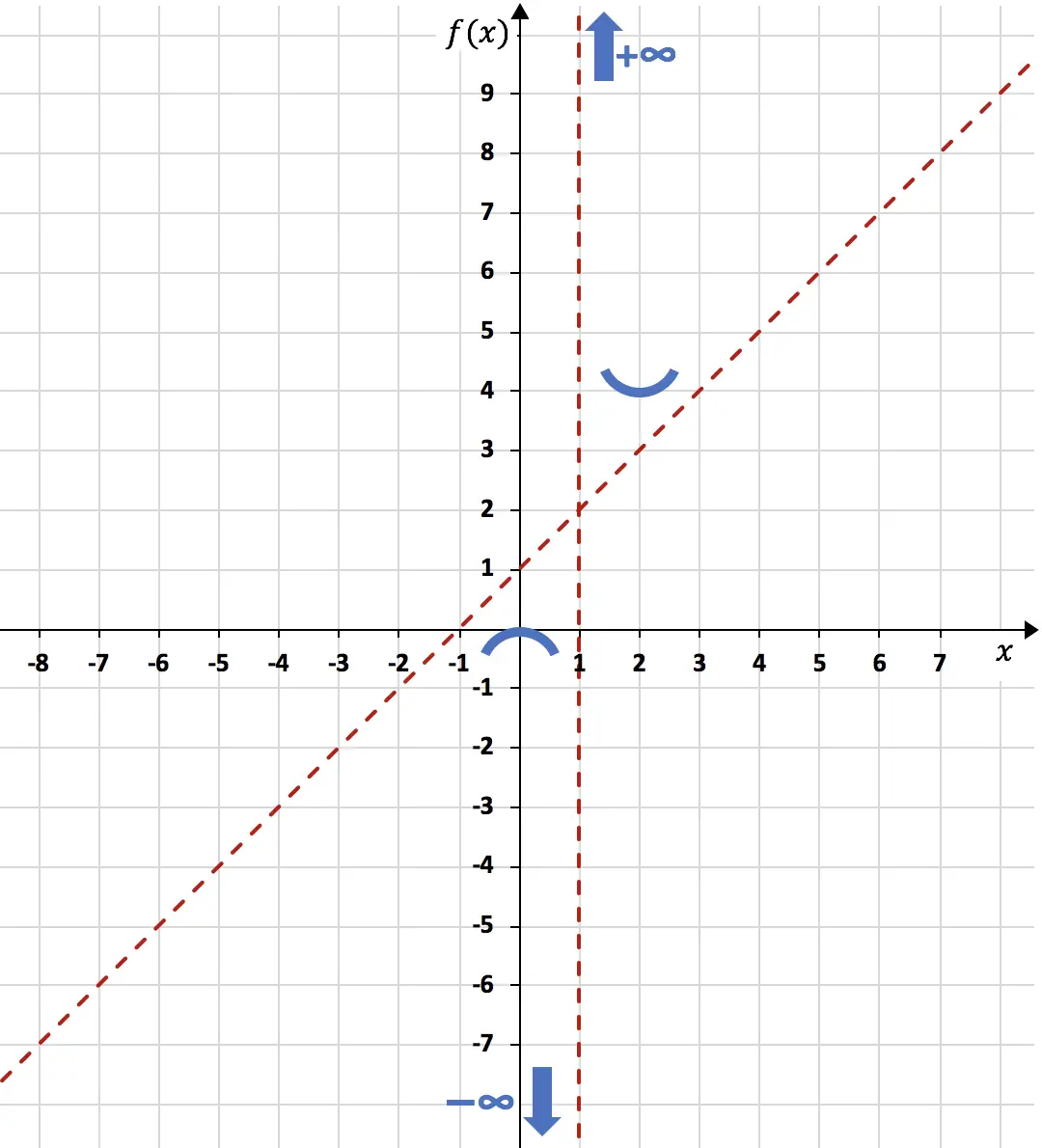
Por fim, basta estudar a curvatura da função , ou seja, estudar os intervalos de concavidade e convexidade da função. Para fazer isso, calculamos sua segunda derivada:

$f'(x)=\cfrac{x^2-2x}{(x-1)^2} \ \longrightarrow \ f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)\cdot 1}{\left(\left(x-1\right)^2\right)^2}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)}{(x-1)^4}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^{\cancel{2}}- (x^2-2x)\cdot 2\cancel{(x-1)}}{(x-1)^{\cancelto{3}{4}}} = \cfrac{(2x-2)\cdot (x-1)- (x^2-2x)\cdot 2}{(x-1)^3}$

$f''(x)= \cfrac{2x^2-2x-2x+2- (2x^2-4x)}{(x-1)^3} =\cfrac{2x^2-2x-2x+2- 2x^2+4x}{(x-1)^3}$

$f''(x) =\cfrac{2}{(x-1)^3}$

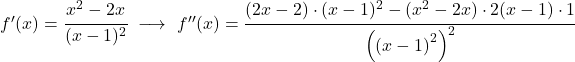
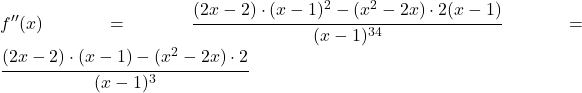
E agora igualamos a segunda derivada a zero e resolvemos a equação:

$f''(x)=0$

$\cfrac{2}{(x-1)^3} =0$

$2=0\cdot \left(x-1\right)^3$

$2=0$

2 nunca será igual a 0, então a equação

$f''(x)=0$

Não há solução.

Representamos agora na reta numérica todos os pontos críticos encontrados, ou seja, os pontos que não pertencem ao domínio (x=1) e aqueles que cancelam a segunda derivada (neste caso não há nenhum):

E avaliamos o sinal da derivada em cada intervalo, para saber se a função é convexa ou côncava. Portanto, pegamos um ponto em cada intervalo (nunca os pontos singulares) e observamos qual sinal a derivada tem neste ponto:

$f''(x) =\cfrac{2}{(x-1)^3}$

$f''(0) =\cfrac{2}{(0-1)^3} = \cfrac{2}{-1}=-2 \ \rightarrow \ \bm{-}$

$f''(2) =\cfrac{2}{(2-1)^3} = \cfrac{2}{1}=2 \ \rightarrow \ \bm{+}$

E finalmente deduzimos os intervalos de concavidade e convexidade da função. Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Os intervalos de concavidade e convexidade são, portanto:

Convexo

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,1)}$

No entanto, embora haja uma mudança na curvatura em x=1, não é um ponto de inflexão. Porque x=1 não pertence ao domínio da função.

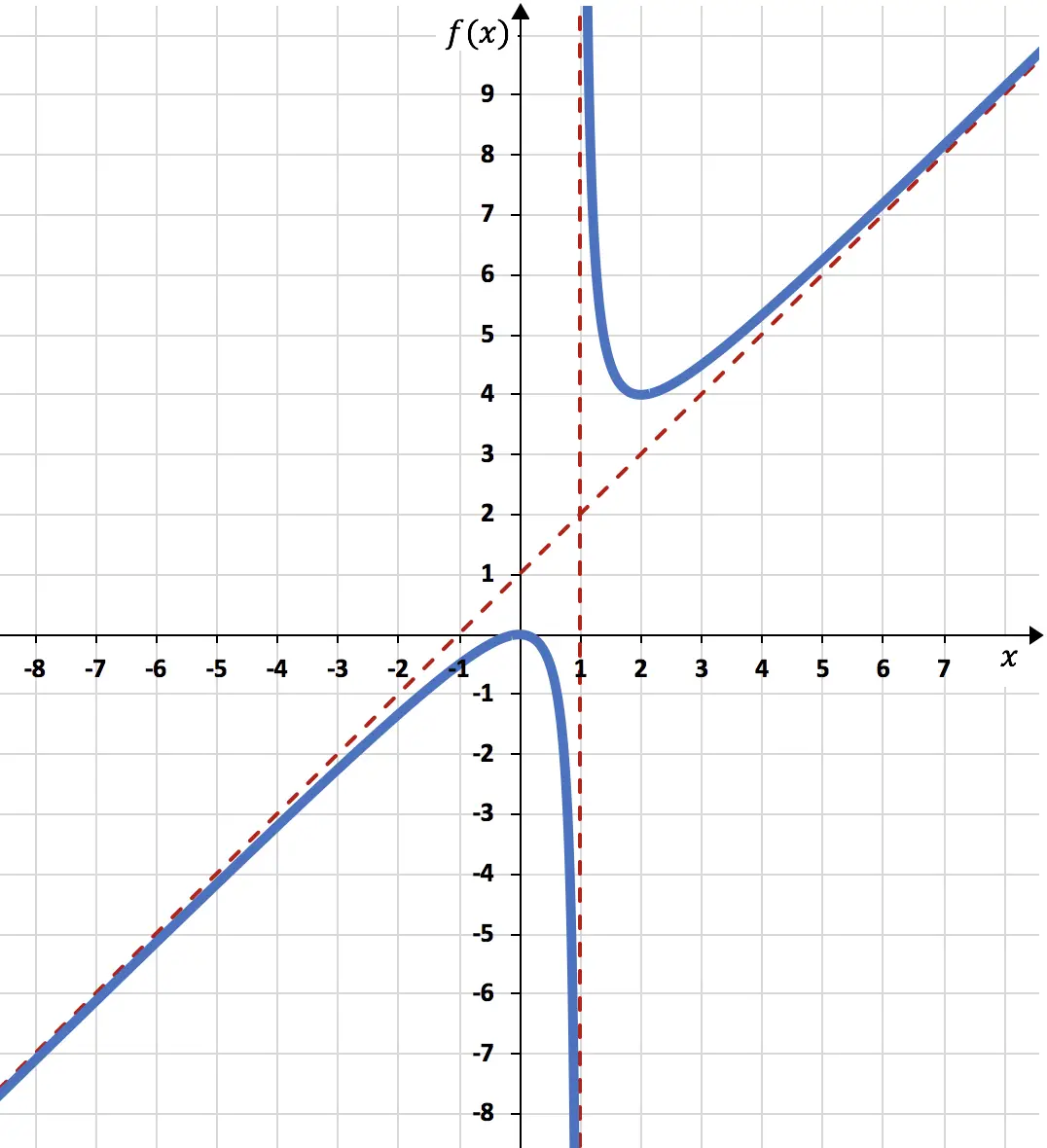
Assim podemos terminar de representar a função usando tudo o que calculamos:

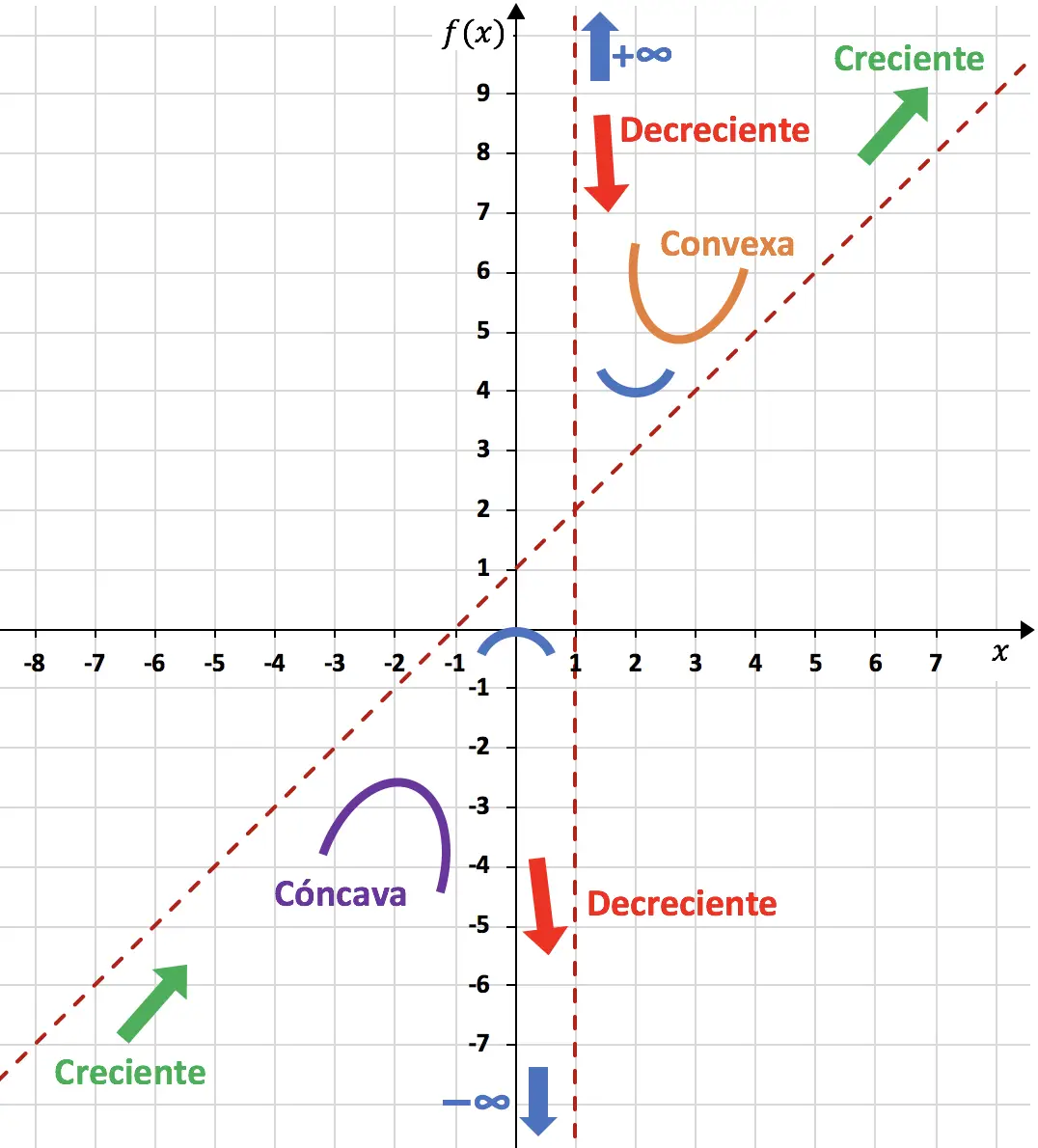
A função representada no gráfico fica assim:

representação gráfica da função racional

Exercícios resolvidos para representar funções

Exercício 1

Faça um gráfico da seguinte função polinomial:

$\displaystyle f(x)=x^3-3x^2+4$

Veja a solução

A primeira coisa a fazer é calcular o domínio de definição da função. Esta é uma função polinomial, portanto o domínio consiste apenas em números reais:

$\text{Dom } f= \mathbb{R}$

Para encontrar o ponto de intersecção com o eixo X, resolvemos

$f(x)= 0.$

$f(x)=0$

$x^3-3x^2+4=0$

Esta é uma equação de grau maior que 2. Portanto, fatoramos a equação:

$(x+1)(x^2-4x+4)=0$

Então x=-1 é uma solução. E calculamos as outras soluções resolvendo a equação quadrática resultante:

$\begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}$

Os pontos de intersecção com o eixo X são, portanto:

$\bm{(-1,0)}$

$\bm{(2,0)}$

E para encontrar o ponto de intersecção com o eixo Y, calculamos

$f(0).$

Como x é sempre 0 no eixo Y:

$f(0)=0^3-3\cdot0^2+4 = 4$

O ponto de intersecção com o eixo Y é, portanto:

$\bm{(0,4)}$

Para ver se a função possui assíntotas verticais, precisamos calcular o limite da função em pontos que não pertencem ao domínio. Neste caso, o domínio inclui todos os números reais. A função, portanto, não tem assíntota vertical.

Por outro lado, a assíntota horizontal da função será o resultado do limite infinito da função. Ainda:

$\displaystyle \lim_{x \to +\infty} \ x^3-3x^2+4 =(+\infty)^3 = +\infty$

O limite infinito da função nos deu +∞, então a função não tem assíntota horizontal.

Agora calculamos a assíntota oblíqua. As assíntotas oblíquas têm a forma

$y=mx+n.$

$m$

É calculado com a seguinte fórmula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \left( x^3-3x^2+4\right): x =$

$\displaystyle = \lim_{x \to +\infty} \cfrac{x^3-3x^2+4}{x} = \cfrac{+\infty}{+\infty} = +\infty$

O limite nos deu +∞, então a função também não possui assíntota oblíqua.

Para estudar a monotonicidade da função, devemos primeiro calcular a sua derivada:

$f(x)= x^3-3x^2+4 \ \longrightarrow \ f'(x)= 3x^2-6x$

Agora definimos a derivada igual a 0 e resolvemos a equação:

$f'(x)= 0$

$3x^2-6x=0$

$x(3x-6)=0$

$\displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}$

Representamos agora na reta numérica todos os pontos singulares obtidos, ou seja, os pontos que não pertencem ao domínio (neste caso, todos pertencem) e aqueles que cancelam a derivada (x=0 e x =2) :

E avaliamos o sinal da derivada em cada intervalo, para saber se a função aumenta ou diminui. Portanto, pegamos um ponto em cada intervalo (nunca os pontos singulares) e observamos qual sinal a derivada tem neste ponto:

$f'(-1)=3(-1)^2-6(-1)= 3+6 = 9\ \rightarrow \ \bm{+}$

$f'(1)=3\cdot 1^2-6\cdot 1= 3-6 = -3\ \rightarrow \ \bm{-}$

$f'(3)=3\cdot 3^2-6\cdot 3= 27-18 = 9\ \rightarrow \ \bm{+}$

Crescimento:

$\bm{(-\infty,0)\cup (2,+\infty)}$

Diminuir:

$\bm{(0,2)}$

A função vai de crescente a decrescente em x=0, então x=0 é o máximo da função. E a função vai de decrescente para crescente em x=2, então x=2 é o mínimo da função.

Finalmente, substituímos os extremos encontrados na função original para encontrar as coordenadas Y dos pontos:

$f(0)=0^3-3\cdot 0^2+4 = 4 \ \longrightarrow \ (0,4)$

$f(2)=2^3-3\cdot 2^2+4 = 8-3 \cdot 4 +4 = 0 \ \longrightarrow \ (2,0)$

Os extremos relativos da função são, portanto:

Máximo no ponto

$\bm{(0,4)}$

Mínimo para apontar

$\bm{(2,0)}$

Para estudar a curvatura da função, calculamos sua segunda derivada:

$f'(x)= 3x^2-6x \ \longrightarrow \ f''(x)= 6x-6$

Agora definimos a segunda derivada igual a 0 e resolvemos a equação:

$f''(x)= 0$

$6x-6=0$

$6x=6$

$x= \cfrac{6}{6} = 1$

Representamos na reta todos os pontos singulares encontrados, ou seja, os pontos que não pertencem ao domínio (neste caso todos pertencem) e aqueles que cancelam a derivada (x=1):

E agora avaliamos o sinal da segunda derivada em cada intervalo, para saber se a função é côncava ou convexa. Portanto, pegamos um ponto em cada intervalo (nunca os pontos singulares) e observamos qual sinal a segunda derivada tem neste ponto:

$f''(0)=6\cdot 0-6= -6 \ \rightarrow \ \bm{-}$

$f''(2)=6\cdot 2-6= 12-6= 6 \ \rightarrow \ \bm{+}$

Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Os intervalos de concavidade e convexidade são, portanto:

Convexo

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Além disso, a função muda de côncava para convexa em x=1, então x=1 é um ponto de inflexão da função.

Finalmente, substituímos os pontos de inflexão encontrados na função original para encontrar a coordenada Y dos pontos:

$f(1)=1^3-3\cdot 1^2+ 4= 1 -3 +4 =2 \ \longrightarrow \ (1,2)$

Os pontos de viragem da função são, portanto:

Pontos de viragem:

$\bm{(1,2)}$

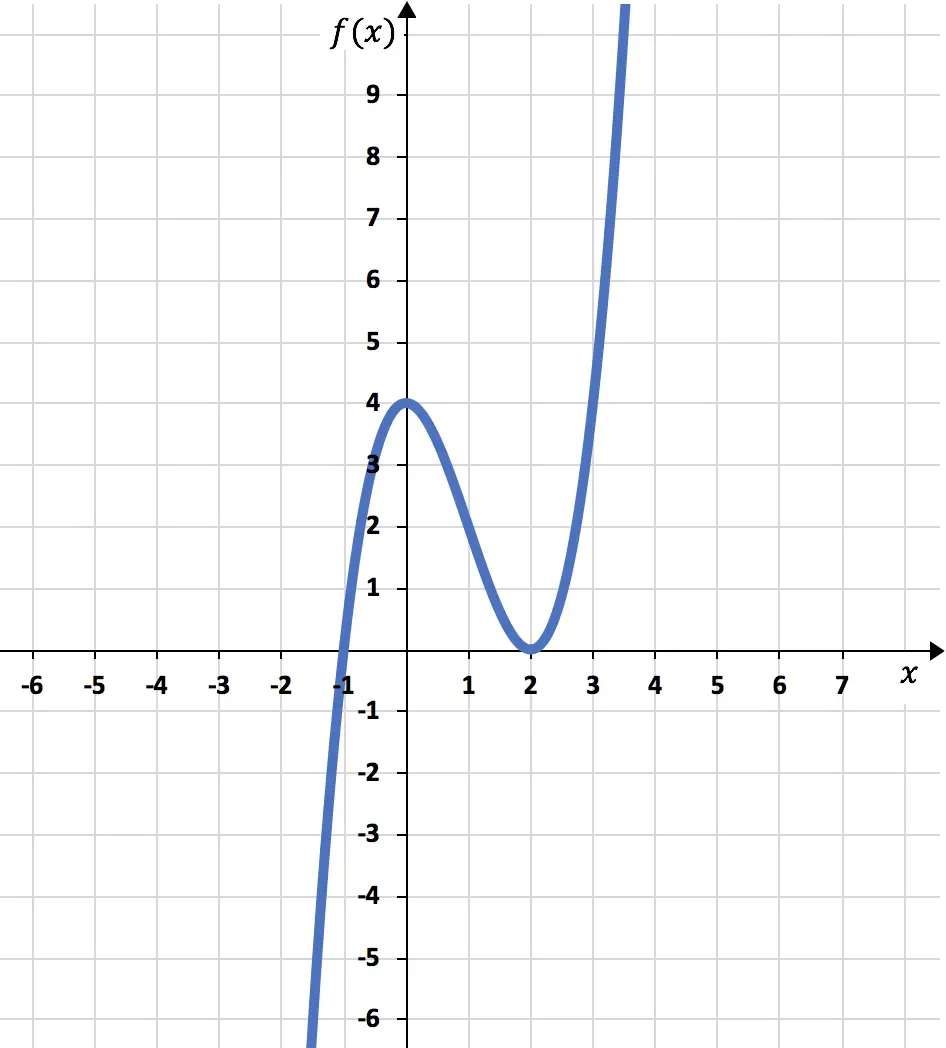
Finalmente, com base em todas as informações que calculamos, representamos graficamente a função:

representação gráfica da função polinomial

Exercício 2

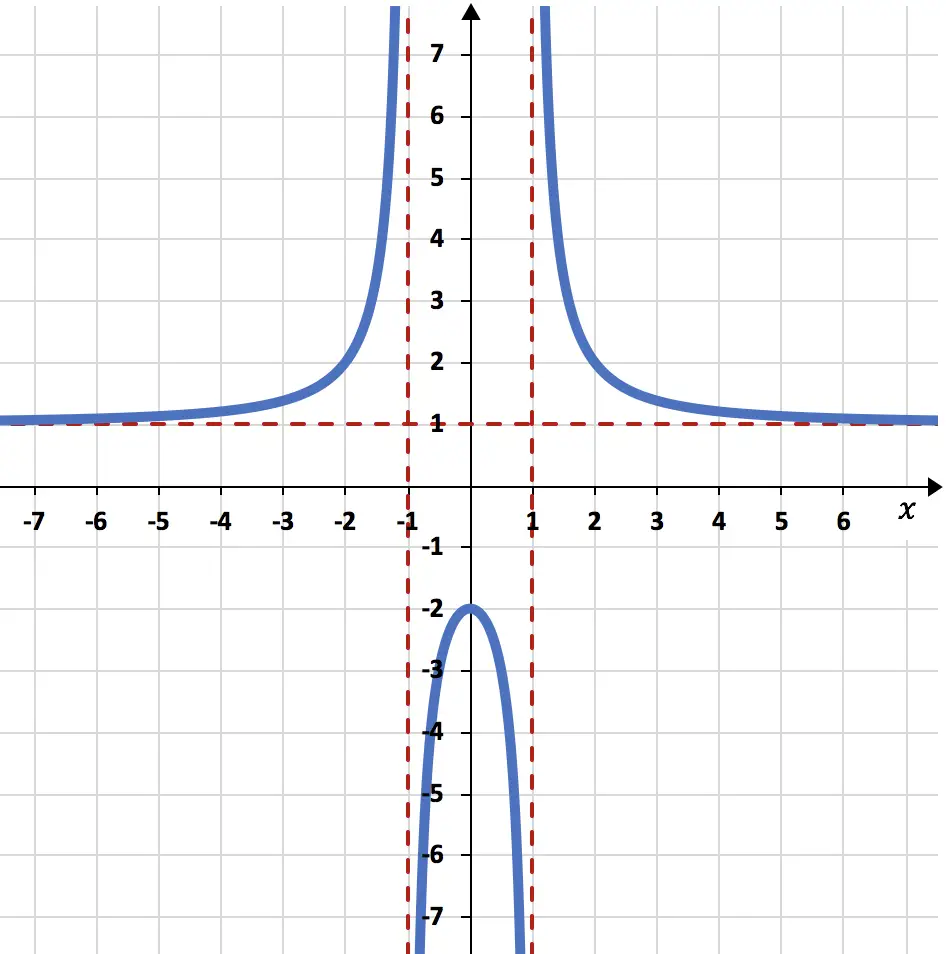
Faça um gráfico da seguinte função racional:

$\displaystyle f(x)=\frac{x^2+2}{x^2-1}$

Veja a solução

Para encontrar o domínio da função, igualamos o denominador. traga a fração para zero e resolva a equação resultante:

$x^2-1= 0$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm 1$

$\text{Dom } f= \mathbb{R}-\{-1, +1 \}$

Segundo, determinamos os limites da função com o eixo x igual à expressão algébrica da função. aço:

$f(x)=0$

$\cfrac{x^2+2}{x^2-1}=0$

$x^2+2=0\cdot (x^2-1)$

$x^2+2=0$

$x^2=-2$

$x=\sqrt{-2} \quad \color{red}\bm{\times}$

Não existe raiz quadrada de um número negativo. Portanto, a função não intercepta o eixo X.

E para encontrar o ponto de intersecção com o eixo do computador, avaliamos a função em x=0.

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2$

O ponto de intersecção com o eixo Y é, portanto:

$\bm{(0,-2)}$

Para ver se a função possui assíntotas verticais, precisamos calcular o limite da função em pontos que não pertencem ao domínio (neste caso x=-1 e x=+1). E se o resultado for infinito, é uma assíntota vertical. Ainda:

$\displaystyle \lim_{x \to -1} \cfrac{x^2+2}{x^2-1} = \cfrac{(-1)^2+2}{(-1)^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

Como o limite da função quando x se aproxima de -1 dá o infinito, x=-1 é uma assíntota vertical.

Calculamos os limites laterais da assíntota x=-1 substituindo um número muito próximo a ela na função:

$\displaystyle f(-1,1)=\cfrac{(-1,1)^2+2}{(-1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to -1^{-}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

$\displaystyle f(-0,9)=\cfrac{(-0,9)^2+2}{(-0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to -1^{+}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

Agora vamos ver se x=+1 é uma assíntota vertical:

$\displaystyle \lim_{x \to +1} \cfrac{x^2+2}{x^2-1} = \cfrac{1^2+2}{1^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

Como o limite da função quando x se aproxima de +1 dá infinito, x=+1 é uma assíntota vertical.

Calculamos os limites laterais da assíntota x=1 substituindo um número muito próximo dela na função:

$\displaystyle f(0,9)=\cfrac{(0,9)^2+2}{(0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to +1^{-}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

$\displaystyle f(1,1)=\cfrac{(1,1)^2+2}{(1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to +1^{+}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

Por outro lado, a assíntota horizontal da função será o resultado do limite infinito da função. Ainda:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2+2}{x^2-1} = \cfrac{+\infty}{+\infty } =\cfrac{1}{1} = 1$

O limite infinito da função nos deu 1, então a função tem uma assíntota horizontal em y=1.

Como a função possui uma assíntota horizontal, ela não terá uma assíntota oblíqua.

Diferenciamos a função e depois estudamos os intervalos de crescimento e diminuição:

$f(x)=\cfrac{x^2+2}{x^2-1} \ \longrightarrow \ f'(x)= \cfrac{2x \cdot (x^2-1) -(x^2+2) \cdot 2x}{\left(x^2-1 \right)^2}$

$f'(x)= \cfrac{2x^3-2x - (2x^3+4x) }{\left(x^2-1 \right)^2} = \cfrac{-6x}{\left(x^2-1 \right)^2}$

Agora definimos a derivada igual a 0 e resolvemos a equação:

$f'(x)= 0$

$\cfrac{-6x}{\left(x^2-1 \right)^2}=0$

$-6x=0\cdot\left(x^2-1 \right)^2$

$-6x= 0$

$x=\cfrac{0}{-6} = 0$

Representamos na reta todos os pontos críticos calculados, que são os pontos que não pertencem ao domínio (x=-1 e x=+1) e aqueles que cancelam a derivada (x=0):

$f'(-2)= \cfrac{-6(-2)}{\left((-2)^2-1 \right)^2} = \cfrac{12}{9} =1,33 \ \rightarrow \ \bm{+}$

$f'(-0,5)= \cfrac{-6(-0,5)}{\left((-0,5)^2-1 \right)^2} = \cfrac{3}{0,56} =5,33 \ \rightarrow \ \bm{+}$

$f'(0,5)= \cfrac{-6\cdot 0,5}{\left(0,5^2-1 \right)^2} = \cfrac{-3}{0,56} =-5,33 \ \rightarrow \ \bm{-}$

$f'(2)= \cfrac{-6\cdot 2}{\left(2^2-1 \right)^2} = \cfrac{-12}{9} =-1,33 \ \rightarrow \ \bm{-}$

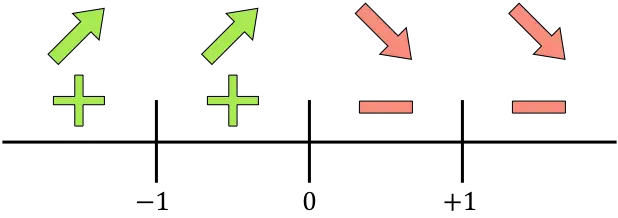
A função aumenta onde a derivada é positiva e a função diminui onde a função é negativa:

Crescimento:

$\bm{(-\infty,-1)\cup (-1,0)}$

Diminuir:

$\bm{(0,1)\cup (1,+\infty)}$

A função vai de crescente a decrescente em x=0, então x=0 é um máximo local da função.

Substituímos o extremo encontrado na função original para encontrar a coordenada Y do ponto:

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2 \ \longrightarrow \ (0,-2)$

Os extremos relativos da função são, portanto:

Máximo no ponto

$\bm{(0,-2)}$

Para estudar a curvatura da função, calculamos sua segunda derivada:

$f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”> <p class=$ Todos os termos têm

$(x^2-1)$

, podemos, portanto, simplificar a fração:

$f''(x)= \cfrac{-6 \left(x^2-1 \right)^{\cancel{2}} + 24x^2\cancel{(x^2-1)}}{\left(x^2-1 \right)^\cancelto{3}{4}} =\cfrac{-6 \left(x^2-1 \right) + 24x^2}{\left(x^2 -1\right)^3}$

$f''(x)= \cfrac{-6x^2+6 + 24x^2}{\left(x^2 -1\right)^3} =\cfrac{18x^2+6}{\left(x^2 -1\right)^3}$

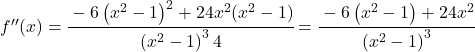
Agora definimos a segunda derivada igual a 0 e resolvemos a equação:

$f''(x)= 0$

$\cfrac{18x^2+6}{\left(x^2 -1\right)^3}=0$

$18x^2+6=0\cdot \left(x^2 -1\right)^3$

$18x^2+6= 0$

$18x^2=-6$

$x^2=\cfrac{-6}{18}$

$x^2=-0,33$

$x=\sqrt{-0,33} \quad \color{red}\bm{\times}$

Não existe raiz quadrada de um número negativo. Então não há ponto que corresponda

$f''(x)=0$

Agora representamos na reta todos os pontos singulares encontrados, ou seja, os pontos que não pertencem ao domínio (x=-1 e x=+1) e aqueles que cancelam a segunda derivada (neste caso não há qualquer):

E avaliamos o sinal da segunda derivada em cada intervalo, para saber se a função é côncava ou convexa. Portanto, pegamos um ponto em cada intervalo (nunca os pontos singulares) e observamos qual sinal a segunda derivada tem neste ponto:

$f''(-2)=\cfrac{18(-2)^2+6}{\left((-2)^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

$f''(0)=\cfrac{18\cdot 0^2+6}{\left(0^2 -1\right)^3}= \cfrac{6}{-1} = -6 \ \rightarrow \ \bm{-}$

$f''(2)=\cfrac{18\cdot 2^2+6}{\left(2^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Os intervalos de concavidade e convexidade são, portanto:

Convexo

$(\bm{\cup})$

$\bm{(-\infty, -1) \cup (1, +\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-1,1)}$

No entanto, embora haja uma mudança na curvatura em x=-1 e em x=1, estes não são pontos de inflexão. Porque eles não pertencem ao domínio da função.

E finalmente, representamos graficamente a função usando todos os cálculos realizados:

Exercício 3

Trace a seguinte função racional em um gráfico:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Veja a solução

Esta é uma função racional, então precisamos igualar o denominador a 0 para ver quais números não pertencem ao domínio da função:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Para encontrar o ponto de intersecção com o eixo X, resolvemos

$f(x)= 0.$

Como a função sempre tem valor 0 no eixo X:

$f(x)=0$

$\cfrac{x^3}{x^2-4}=0$

$x^3=0\cdot (x^2-4)$

$x^3=0$

$x=\sqrt[3]{0}=0$

O ponto de intersecção com o eixo X é, portanto:

$\bm{(0,0)}$

E para encontrar o ponto de intersecção com o eixo Y, calculamos

$f(0).$

Como x é sempre 0 no eixo Y:

$f(0)=\cfrac{0^3}{0^2-4} = \cfrac{0}{-4} = 0$

O ponto de intersecção com o eixo Y é, portanto:

$\bm{(0,0)}$

Neste caso, o ponto de intersecção com o eixo X coincide com o ponto de intersecção com o eixo Y, pois a função passa pela origem das coordenadas.

Para ver se a função possui assíntotas verticais, precisamos calcular o limite da função em pontos que não pertencem ao domínio (neste caso x=-2 e x=+2). E se o resultado for infinito, é uma assíntota vertical. Ainda:

$\displaystyle \lim_{x \to -2} \cfrac{x^3}{x^2-4} = \cfrac{(-2)^3}{(-2)^2-4} =\cfrac{-8}{4-4}= \cfrac{-8}{0} = \infty$

Como o limite da função quando x se aproxima de -2 dá infinito, x=-2 é uma assíntota vertical.

Calculamos os limites laterais da assíntota x=-2 substituindo um número muito próximo a ela na função:

$\displaystyle f(-2,1)=\cfrac{(-2,1)^3}{(-2,1)^2-4} =-22,59 \longrightarrow \lim_{x \to -2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(-1,9)=\cfrac{(-1,9)^3}{(-1,9)^2-4} =+17,59 \longrightarrow \lim_{x \to -2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Agora vamos ver se x=+2 é uma assíntota vertical:

$\displaystyle \lim_{x \to +2} \cfrac{x^3}{x^2-4} = \cfrac{(2)^3}{(2)^2-4} =\cfrac{8}{4-4}= \cfrac{8}{0} = \infty$

Como o limite da função quando x se aproxima de +2 dá infinito, x=+2 é uma assíntota vertical.

Calculamos os limites laterais da assíntota x=2 substituindo um número muito próximo dela na função:

$\displaystyle f(1,9)=\cfrac{1,9^3}{1,9^2-4} =-17,59 \longrightarrow \lim_{x \to 2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(2,1)=\cfrac{2,1^3}{2,1^2-4} =22,59 \longrightarrow \lim_{x \to 2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Por outro lado, a assíntota horizontal da função será o resultado do limite infinito da função. Ainda:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^3}{x^2-4} = \cfrac{+\infty}{+\infty } =+\infty$

O limite infinito da função nos deu +∞, então a função não tem assíntota horizontal.

Agora calculamos a assíntota oblíqua. As assíntotas oblíquas têm a forma

$y=mx+n.$

$m$

É calculado com a seguinte fórmula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: x =\lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: \frac{x}{1}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3\cdot 1}{(x^2-4)\cdot x} =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x} = \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Uma vez conhecida a inclinação da assíntota oblíqua, determinamos a interceptação usando a seguinte fórmula:

$\displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]$

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Mas obtemos a indeterminação ∞ – ∞. É, portanto, necessário reduzir os termos a um denominador comum. Para fazer isso, multiplicamos e dividimos x pelo denominador da fração:

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]$

$\displaystyle n = \lim_{x \to +\infty} \cfrac{x^3- (x^3-4x)}{x^2-4} = \lim_{x \to +\infty} \cfrac{4x}{x^2-4}$

$\displaystyle n =\lim_{x \to +\infty} \cfrac{4x}{x^2-4} = \cfrac{+\infty}{\infty} =\bm{0}$

Resumindo, a assíntota oblíqua é:

$y = mx+n$

$y = 1x + 0$

$\bm{y = x }$

Para estudar a monotonicidade da função, devemos primeiro calcular a sua derivada:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Agora definimos a derivada igual a 0 e resolvemos a equação:

$f'(x)= 0$

$\cfrac{x^4-12x^2}{\left(x^2-4\right)^2}=0$

$x^4-12x^2=0\cdot \left(x^2-4\right)^2$

$x^4-12x^2=0$

$x^2(x^2-12)=0$

$\displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}$

Representamos agora na reta todos os pontos singulares encontrados, ou seja, os pontos que não pertencem ao domínio (x=-2 e x=+2) e aqueles que cancelam a derivada (x=0, x=- 3,46 e x = +3,46):

$f'(-4)= \cfrac{(-4)^4-12(-4)^2}{\left((-4)^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

$f'(-3)= \cfrac{(-3)^4-12(-3)^2}{\left((-3)^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(-1)= \cfrac{(-1)^4-12(-1)^2}{\left((-1)^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(1)= \cfrac{1^4-12\cdot1^2}{\left(1^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(3)= \cfrac{3^4-12\cdot 3^2}{\left(3^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(4)= \cfrac{4^4-12\cdot 4^2}{\left(4^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

Crescimento:

$\bm{(-\infty,-3,46)\cup (3,46,+\infty)}$

Diminuir:

$\bm{(-3,46,-2)\cup(-2,0)\cup (0,2) \cup (2,3,46)}$

A função vai de aumentar para diminuir em x=-3,46, então x=-3,46 é o máximo da função. E a função vai de decrescente para crescente em x=3,46, então x=3,46 é o mínimo da função.

Determinamos as coordenadas Y das extremidades relativas:

$f(-3,46)=\cfrac{(-3,46)^3}{(-3,46)^2-4} = \cfrac{-41,42}{7,97}=-5,20 \ \longrightarrow \ (-3,46,-5,20)$

$f(3,46)=\cfrac{3,46^3}{3,46^2-4} = \cfrac{41,42}{7,97}=5,20 \ \longrightarrow \ (3,46,5,20)$

Os extremos relativos da função são, portanto:

Máximo no ponto

$\bm{(-3,46,-5,20)}$

Mínimo para apontar

$\bm{(3,46,5,20)}$

Para estudar a curvatura da função, calculamos a segunda derivada da função:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Agora definimos a segunda derivada igual a 0 e resolvemos a equação:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

$x(8x^2+96)=0$

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Não há solução, pois não existe raiz negativa de um número real.

Representamos agora na reta todos os pontos singulares encontrados, ou seja, os pontos que não pertencem ao domínio (x=-2 e x=+2) e aqueles que cancelam a segunda derivada (x=0):

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot 1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Os intervalos de concavidade e convexidade são, portanto:

Convexo

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

No entanto, embora haja uma mudança na curvatura em x=-2 ex=+2, estes não são pontos de inflexão. Porque x=-2 e x=+2 não pertencem ao domínio da função. Por outro lado, em x=0 há uma mudança na curvatura (a função passa de convexa para côncava) e isso pertence à função, então x=0 é um ponto de inflexão.

Substituímos os pontos de inflexão encontrados na função original para encontrar a outra coordenada do ponto de inflexão:

$f(0) = \cfrac{0^3}{0^2-4} = \cfrac{0}{-4} =0\ \longrightarrow \ (0,0)$

Os pontos de viragem da função são, portanto:

Pontos de viragem:

$\bm{(0,0)}$

Finalmente, com base em todas as informações que calculamos, representamos a função:

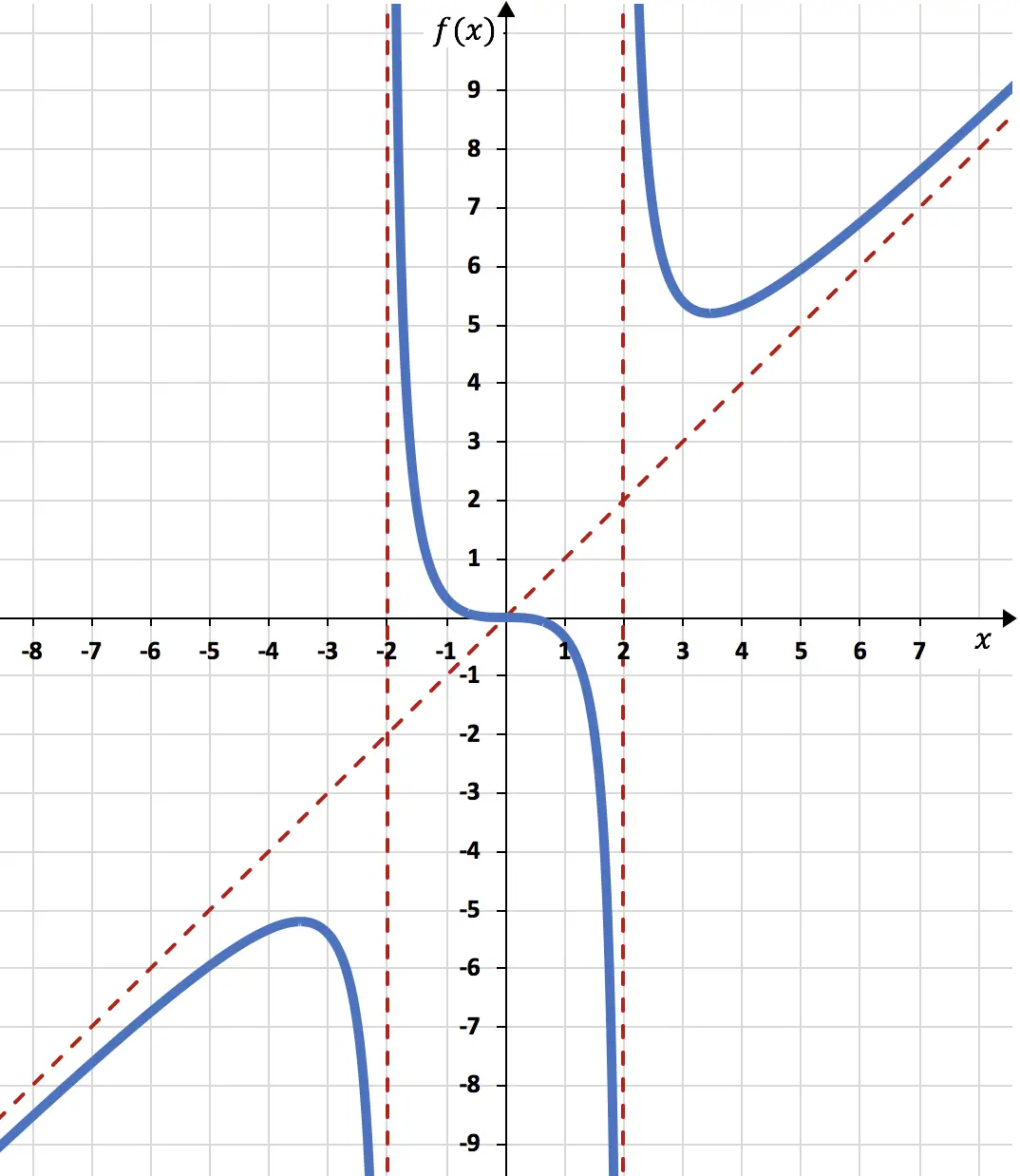
representação gráfica de funções resolvidas, exercícios

Comentário: Observe que a função cruza a assíntota oblíqua no ponto

$(0,0) .$

Na verdade, as assíntotas oblíquas determinam sobretudo o comportamento da função quando x tende para +∞ e -∞, de fato, a função nunca cruza a assíntota oblíqua à direita do gráfico (x→+∞) e à esquerda de o gráfico (x→-∞). Porém, é muito raro que a função cruze a assíntota oblíqua no meio, é um caso muito especial.

Representação de função

Como representar uma função em um gráfico

Exemplo de representação de uma função

Exercícios resolvidos para representar funções

Exercício 1

Exercício 2

Exercício 3

Deixe um comentário Cancelar resposta